点动型探究题
1.点在直线上运动
1. 解：（1）不变. ………………………………………………………………1分
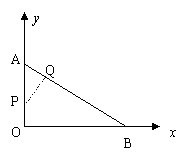
理由：在直角三角形中，斜边上的中线等于斜边的一半，因为斜边AB不变，所以斜边上的中线OP不变. ………3分
（2）当△AOB的斜边上的高h等于中线OP时，△AOB的面积最大. ………………………………4分
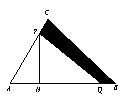
如图，若h与OP不相等，则总有h<OP，
故根据三角形面积公式，有h与OP相等时△AOB的面积最大. …………………………………5分
此时，S△AOB=
.
所以△AOB的最大面积为
. ……………6分
2.2005年无锡市
解、（1）证∠APE=∠ADQ，∠AEP=∠AQD.
（2）注意到△APE∽△ADQ与△PDE∽△ADQ，及S△PEF=
，得S△PEF=
=
. ∴当
，即P是AD的中点时，S△PEF取得最大值
.
（3）作A关于直线BC的对称点A′，连DA′交BC于Q，则这个点Q就是使△ADQ周长最小的点，此时Q是BC的中点.
3.解、解：（１）设直线AB的解析式为y＝kx＋b
由题意，得 b＝6
8k＋b＝0
解得 k＝－
b＝6
所以，直线AB的解析式为y＝－x＋6． ………２分
（２）由 AO＝6， BO＝8 得 AB＝10
所以AP＝t ，AQ＝10－2t
1° 当∠APQ＝∠AOB时，△APQ∽△AOB．
所以 
＝
解得 t＝
(秒) ………４分
2° 当∠AQP＝∠AOB时，△AQP∽△AOB．
所以 
＝
解得 t＝
(秒) ………６分
（３）过点Q作QE垂直AO于点E．
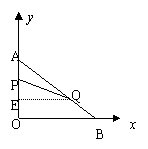在Rt△AOB中，Sin∠BAO＝
＝
…………７分
在Rt△AEQ中，QE＝AQ·Sin∠BAO＝(10-2t)·＝8－
t
所以，S△APQ＝
AP·QE＝t·(8－t)
＝－
＋4t＝
……………………９分
解得t＝2（秒）或t＝3（秒）． ……………………10分
（注：过点P作PE垂直AB于点E也可，并相应给分）
1.
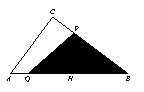
.解：（1）S△PCQ＝
PC·CQ＝
＝
＝2， ………1分
解得 
＝1，
＝2
………2分
∴当时间
为1秒或2秒时，S△PCQ＝2厘米2； ………3分
（2）①当0＜≤2时，S＝
＝
； ………5分
②当2＜≤3时， S＝
＝
；………7分
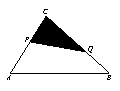
③当3＜≤4.5时，S＝
＝
；…9分
（3）有； ………10分
①在0＜≤2时，当＝
，S有最大值，S1＝
； ………11分
②在2＜≤3时，当＝3，S有最大值，S2＝
； ………12分
③在3＜≤4.5时，当＝
，S有最大值，S3＝
； ………13分
∵S1＜S2＜S3 ∴＝时，S有最大值，S最大值＝． ………14分
2.解⑴C（2a，0），……………………………………………1分
D（0，2a+8）………………………………………………………………2分
⑵方法一：由题意得：A（－4，0），B（0，4）
－4＜a＜0，且a≠2，………………………………………………………………3分
① 当2a+8＜4，即－4＜a＜－2时
AC=－4－2a，BD=4－（2a+8）=－4－2a
∴AC=BD……………………………………………………………………………5分
② 当2a+8＞4，即－2＜a＜0时
同理可证：AC=BD
综上：AC=BD……………………………………………………………………………6分
方法二：①当点D在B、O之间时，
连CD，∵∠COD＝90°
∴圆心M在CD上，………………………………………………………………3分
过点D作DF∥AB，
∵点M为CD中点，
∴MA为△CDF中位线，
∴AC＝AF，…………………………………………………………………………4分
又DF∥AB，
∴
，
而BO＝AO
∴AF=BD
∴AC＝BD……………………………………………………………………………5分
②点D在点B上方时，同理可证：AC=BD
综上：AC=BD…………………………………………………………………………6分
⑶方法一
①A(－4,0)，B(0，4)，D(0，2a+8)，M(a，a+4)，△BDE、△ABO均为等腰直角三角形，
E的纵坐标为a+6，∴ME=
(yE－yM)=[a+6-(a+4)]=2…………………7分
AB=4…………………………………………………………………………8分
∴AB=2ME…………………………………………………………………………9分
②AM=( yM－yA)＝(a+4)，BE=yE－yB=a+2，……………………10分
∵AM=BE
又－4＜a＜0，且a≠2，
10 当－4＜a＜－2时
(a+4)= －(a+2)
∴a=－3
M（－3，1）………………………………………………………………………11分
20 当－2＜a＜0时
(a+4)= (a+2)
∴a不存在………………………………………………………………………12分
方法二：
①当点D在B、O之间时，作MP⊥x轴于点P、MQ⊥y轴于点Q，取AB中点N，
在Rt△MNO与Rt△DEM中，MO＝MD
∠MON＝450－∠MOP
∠EMD＝450－∠DMQ＝450－∠OMQ＝450－∠MOP
∴∠MON＝∠EMD
∴Rt△MNO≌Rt△DEM………………………………………………………………7分
∴MN＝ED＝EB
∴AB＝2NB＝2（NE＋EB）＝2（NE＋MN）＝2ME…………………………8分
当点D在点B上方时，同理可证………………………………………………9分
②当点D在B、O之间时，
由①得MN=EB，
∴AM=NE ……………………………………………………………………10分
若AM=BE，则AM=MN=NE=EB=
AB=
∴M（－3，1）……………………………………………………………………11分
点D在点B上方时，不存在。…………………………………………………12分
注：（2）、（3）两问凡需要讨论而没有讨论的，每漏讨论一次扣1分。