拱墅区2006年初中学业水平考试
数学试卷
考试时间90分钟 满分100分
一、选择题(每小题3分,共30分)
1.-2的相反数是( )
A.2
B.![]() C.-
C.-![]() D.-2
D.-2
2.我国18岁以下的未成年人约有367 000 000人,此数据用科学记数法可表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.下列空间图形中,圆柱体是( )
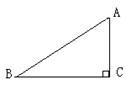
4.如图,在Rt△ABC中,AC=3,BC=4,AB=5,则tanB的值是( )
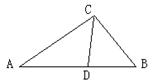
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 5.不等式组
5.不等式组![]() 的解集为(
)
的解集为(
)
A.![]() B.
B.![]() C.
C.![]() D.无解
D.无解
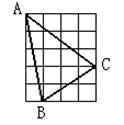
6. 如图,正方形网格中,每个小正方形的边长为1,则网格上△ABC的三条边长中,边长是无理数的有( )
A.0条 B.1条 C.2条 D.3条
7.在100件产品中,已知有2件是不合格产品,从中任意抽取1件,抽到恰好是不合格产品的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.已知点A(1,2)在反比例函数![]() 的图象上,则该反比例函数的解析式是( )
的图象上,则该反比例函数的解析式是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 9.如图,⊙O是△ABC的外接圆,且∠BAO=25°,则∠C的
9.如图,⊙O是△ABC的外接圆,且∠BAO=25°,则∠C的
大小为( )
A.25° B.50° C.60° D.65°
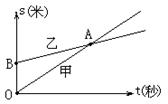 10.如图,OA、BA分别表示甲、乙两名学生跑步的路程s和时间t关系的图象,根据图象判断甲、乙速度快慢,正确的是( )
10.如图,OA、BA分别表示甲、乙两名学生跑步的路程s和时间t关系的图象,根据图象判断甲、乙速度快慢,正确的是( )
A.乙快 B.甲快 C.一样快 D.无法判断
二、填空题(每小题4分,共32分)
11.计算:① 2-5= ;②
![]() = .
= .
12.分解因式 ![]() = .
= .
13.方程![]() 的解是
.
的解是
.
14. 若半径分别为3和8的两个圆相切,则它们的圆心距为 .
15. 某公司共有10名销售人员,去年完成的销售额数据(万元)如下表:
 3,4,4,4,5,5,6,7,8,10
3,4,4,4,5,5,6,7,8,10
则他们销售额的平均数、众数分别是 、 .
 16.如图,已知△ABC中,D是AB边上的一点,连结CD,要使△ABC∽△ACD,只需添加条件
(写出一种适合的条件即可).
16.如图,已知△ABC中,D是AB边上的一点,连结CD,要使△ABC∽△ACD,只需添加条件
(写出一种适合的条件即可).
17.如图,DE是⊙O的直径,弦AB⊥DE,垂足为C,请你在图中找出具有相等关系的结论 (不再添加辅助线,至少写出4对等量关系).
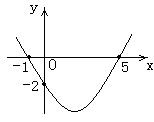 18.已知二次函数
18.已知二次函数![]() 的图象如图所示,有下列结论: ① a>0 ;② 对称轴是x=2 ;③ a、b 同号 ;④ 当x=1和 x=3时,函数值相等; ⑤ 4a+b=0;
的图象如图所示,有下列结论: ① a>0 ;② 对称轴是x=2 ;③ a、b 同号 ;④ 当x=1和 x=3时,函数值相等; ⑤ 4a+b=0;
⑥ 当y=-2时, x的值只有一个. 则正确结论的序号是
(将正确的全写上)
三、解答题(共38分)
19. (本题满分8分)
某报社为了了解读者对一种报纸四个版面的喜欢情况,对读者进行了一次问卷调查,要求读者选出自己最喜欢的一个版面.将所得数据整理后绘制成了如下的条形统计图.
(1)请写出从条形统计图中获得的一条信息;
(2)根据条形中数据补全扇形统计图(要求第二版与第三版相邻)
(3)根据上述数据,对该报社提出一条合理建议。

20.(本题满分10分)
如图,平面直角坐标系中,△ABC是边长为2的正三角形,其中点A、B的坐标分别为(-3,0)、(-3,-2),请按下列要求进行操作和探索:
(1)以y轴为对称轴作△ABC的对称图形△A1B1C1,(不写作法,保留痕迹);
(2)以x轴为对称轴作△A1B1C1的对称图形△A2B2C2,(不写作法,保留痕迹);
(3)直接写出点A1 、B2的坐标;
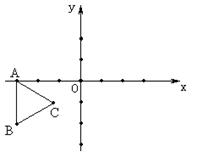 (4)探索:能否通过一次旋转将△ABC旋转到△A2B2C2的位置?你若认为能,请作出肯定回答,并指出这时的旋转中心和旋转的角度;你若认为不能,请作出否定回答(不必说明理由).
(4)探索:能否通过一次旋转将△ABC旋转到△A2B2C2的位置?你若认为能,请作出肯定回答,并指出这时的旋转中心和旋转的角度;你若认为不能,请作出否定回答(不必说明理由).
21. (本题满分10分)
某校初三(1)班40名学生为“希望学校”捐赠图书共100册,捐书的情况如下表:
| 捐书(册) | 1 | 2 | 3 | 4 |
| 人 数 | 6 | ∥∥ | ∥∥ | 7 |
表格中捐2册和3册的人数看不清了,班长要求出捐2册和3册图书的学生各是多少人. 你可以帮他从下面步骤分析、填空、求解:
(1)设捐2册书的有x人、捐3册书的有y人,则x+y= 人;
(2)捐2册和3册书的人共捐书100-(1×6+4×7)= 册;
(3)根据以上分析,列方程组得 ;
(4)解这个方程组得 ;
(5)答:
22. (本题满分10分)
如图,Rt△OAC是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点C在y轴上,OC=![]() ,∠CAO=30°:
,∠CAO=30°:
(1)求OA的长并写出点A的坐标;
(2)求AC所在直线的解析式;
(3)如图,将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE,,求四边形OEDC的面积.
