圆
学校 姓名
一、知识点
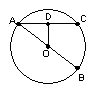
1、与圆有关的角——圆心角、圆周角
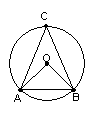（1）图中的圆心角
；圆周角
；
（2）如图，已知∠AOB=50度，则∠ACB= 度；
（3）在上图中，若AB是圆O的直径，则∠AOB= 度；
2、圆的对称性：
（1）圆是轴对称图形，其对称轴是任意一条 的直线；
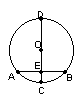圆是中心对称图形，对称中心为
．
（2）垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧．
如图，∵CD是圆O的直径，CD⊥AB于E
∴ = ， =
3、点和圆的位置关系有三种：点在圆 ，点在圆 ，点在圆 ；
例1：已知圆的半径r等于5厘米，点到圆心的距离为d，
（1）当d=2厘米时，有d r，点在圆
（2）当d=7厘米时，有d r，点在圆
（3）当d=5厘米时，有d r，点在圆
4、直线和圆的位置关系有三种：相 、相 、相 ．
例2：已知圆的半径r等于12厘米，圆心到直线l的距离为d，
（1）当d=10厘米时，有d r，直线l与圆
（2）当d=12厘米时，有d r，直线l与圆
（3）当d=15厘米时，有d r，直线l与圆
5、圆与圆的位置关系：
例3：已知⊙O1的半径为6厘米，⊙O2的半径为8厘米，圆心距为 d，
则：R+r= ， R－r= ；
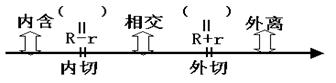（1）当d=14厘米时，因为d R+r，则⊙O1和⊙O2位置关系是：
（2）当d=2厘米时， 因为d R－r，则⊙O1和⊙O2位置关系是：
（3）当d=15厘米时，因为 ，则⊙O1和⊙O2位置关系是：
（4）当d=7厘米时， 因为 ，则⊙O1和⊙O2位置关系是：
（5）当d=1厘米时， 因为 ，则⊙O1和⊙O2位置关系是：
6、切线性质：
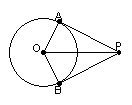例4：（1）如图，PA是⊙O的切线，点A是切点，则∠PAO= 度
（2）如图，PA、PB是⊙O的切线，点A、B是切点，
则 = ，∠ =∠ ；
7、圆中的有关计算
（1）弧长的计算公式：
例5：若扇形的圆心角为60°，半径为3，则这个扇形的弧长是多少？
解：因为扇形的弧长=
所以
==
(答案保留π)
（2）扇形的面积：
例6：①若扇形的圆心角为60°，半径为3，则这个扇形的面积为多少？
解：因为扇形的面积S= 
所以S==
(答案保留π)
②若扇形的弧长为12πcm，半径为6㎝，则这个扇形的面积是多少？
解：因为扇形的面积S=
所以S= =
（3）圆锥：
例7：圆锥的母线长为5cm，半径为4cm，则圆锥的侧面积是多少？
解：∵圆锥的侧面展开图是 形，展开图的弧长等于
∴圆锥的侧面积=
8、三角形的外接圆的圆心——三角形的外心——三角形的 交点；
三角形的内切圆的圆心——三角形的内心——三角形的 交点；
例8：画出下列三角形的外心或内心
（1）画三角形ABC的内切圆， （2）画出三角形
DEF的外接圆，
并标出它的内心； 并标出它的外心
二、练习：
（一）填空题
1、如图，弦AB分圆为1：3两段，则
的度数=
度，
的度数等于 度；∠AOB＝ 度，∠ACB＝ 度，
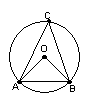
2、如图，已知A、B、C为⊙O上三点，若、
、
的
度数之比为1∶2∶3，则∠AOB＝ ，∠AOC＝ ，
∠ACB＝
，
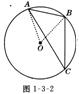3、如图1－3－2，在⊙O中，弦AB=1.8cm，圆周角∠ACB=30○ ，
则 ⊙O的半径等于=_________cm．
4、⊙O的半径为5，圆心O到弦AB的距离OD=3，
则AD= ，AB的长为 ；
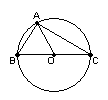
5、如图，已知⊙O的半径OA=13㎝，弦AB＝24㎝，
则OD=
㎝。
6、如图,已知⊙O的直径AB＝10cm，弦AC＝8cm,
则弦心距OD等于 cm.
7、已知：⊙O1的半径为3，⊙O2的半径为4，若⊙O1与⊙O2
外切，则O1O2＝ 。
8、已知：⊙O1的半径为3，⊙O2的半径为4，若⊙O1与⊙O2内切，则O1O2＝ 。
9、已知：⊙O1的半径为3，⊙O2的半径为4，若⊙O1与⊙O2相切，则O1O2＝ 。
10、已知：⊙O1的半径为3，⊙O2的半径为4，若⊙O1与⊙O2相交，则两圆的圆心距
d的取值范围是
11、已知⊙O1和⊙O2外切，且圆心距为10cm，若⊙O1的半径为3cm，则⊙O2的半径
为_____ ___cm．
12、已知⊙O1和⊙O2内切，且圆心距为10cm，若⊙O1的半径为3cm，则⊙O2的半径
为______ __cm．
13、已知⊙O1和⊙O2相切，且圆心距为10cm，若⊙O1的半径为3cm，则⊙O2的半径
为______ _cm．
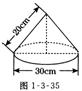14、如图1－3－35是小芳学习时使用的圆锥形台灯灯罩的示意图，
则围成这个灯罩的铁皮的面积为________cm2 (不考虑接缝等因
素，计算结果用π表示）．
15、如图，两个同心圆的半径分别为２和１，∠AOB=
,
则阴影部分的面积是_________
16、一个圆锥的母线与高的夹角为30°，那么这个圆锥的侧面展开图中扇形的弧长
与半径的比是
（二）选择题
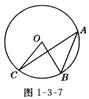1、如图1－3－7，A、B、C是⊙O上的三点，∠BAC=30°
则∠BOC的大小是（ ）
A．60○ B．45○ C．30○ D．15○
2、如图，AB为⊙O的直径，C、D是⊙O上的两点，∠BAC＝20°，
＝
，
则∠DAC的度数是(
)
(A)30° (B) 35° (C) 45° (D) 70°
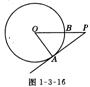3、如图1－3－16，PA为⊙O的切线，A为切点，PO交 ⊙O于
点B，PA=4，OA=3，则cos∠APO的值为（ ）
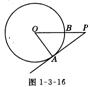4、PA切⊙O于A，PA = 
，∠APO = 30
，则PO的为（ ）
A 
B 2
C 1
D 
5、圆柱的母线长5cm，为底面半径为1cm，则这个圆拄的侧面积是（ ）
A．10cm2 B．10πcm2 C．5cm2 D．5πcm2
6、如图，一个圆柱形笔筒，量得笔筒的高是20cm，底面圆的半径为5cm，
那么笔筒的侧面积为( )
A.200cm2 B.100πcm2 C.200πcm2 D.500πcm2
7、制作一个底面直径为30cm，高40cm的圆柱形无盖铁桶，所需铁皮至少为（ ），
A．1425πcm2 B．1650πcm2 C．2100πcm2 D．2625πcm2
8、已知圆锥的底面半径为3，高为4，则圆锥的侧面积为（ ）
（A）10π （B）12π （C）15π （D）20π
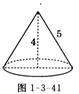9、如图，圆锥的母线长为5cm，高线长为4cm，则圆锥的底面积是（ ）
A．3πcmZ B．9πcmZ C．16πcmZ D．25πc
10、如图，若四边形ABCD是半径为1cm的⊙O的内接正方形，
则图中四个弓形（即四个阴影部分）的面积和为（ ）．
（A）
（B）
（C）
（D）
（三）解答题
1、如图，直角三角形ABC是⊙O的内接三角形，∠ACB=90°，∠A=30°，过点C
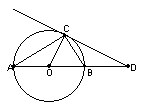作⊙O的切线交AB的延长线于点D，连结CO。请写出六个你认为正确的结论；
（不准添加辅助线）；
解：（1） ；
（2） ；
（3） ； （4） ；
（5） ； （6） ；
2、⊙O
和⊙O
半径之比为
，当OO= 21 cm时，两圆外切，当两圆内切时，
OO的长度应多少？
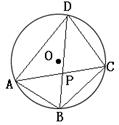3、如图，⊙O的内接四边形ABCD的对角线交于P,已知AB＝BC，
求证：△ABD∽△DPC
4、如图，PA、PB是⊙O的切线，点A、B为切点，AC是⊙O的直径，∠BAC=20°，
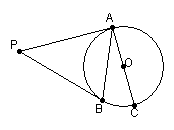求∠P的度数。
5、以点O（3，0）为圆心，5个单位长为半径作圆，并写出圆O与坐标轴的交点坐标；
解：圆O与x轴的交点坐标是：
圆O与y轴的交点坐标是：
6、如图，半圆的半径为2cm，点C、D三等分半圆，求阴影部分面积
 |
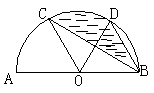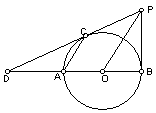7、如图，AB是⊙O的直径，PB与⊙O相切与点B，弦AC∥OP，PC交BA的延长线于点D，求证：PD是⊙O的切线，
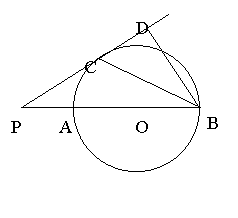8、已知：如图，AB是⊙O的直径，点P在BA的延长线上，PD切⊙O于点C，BD⊥PD，垂足为D，连接BC。
求证：（1）BC平分∠PBD；
（2）
。
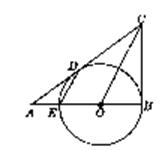9、如图，CB、CD是⊙O的切线，切点分别为B、D，CD的延长线与⊙O的
直径BE的延长线交于A点，连OC，ED．
（1）探索OC与ED的位置关系，并加以证明；
（2）若OD＝4，CD=6，求tan∠ADE的值．
圆 答案
一、知识点：
1、（1）∠AOB ∠ACB （2）25； （3）90；
2、（1）直径所在的直线；圆心 （2）AE=BE，弧AC=弧BC；
3、内，上，外，例1：（1）<，内；（2），> ，外，（3）=，上；
4、交，切，离 例2：（1）<，相交；（2）， =，相切，（3）>，相离；
5、例3：14，2；（1）=，外切；（2）=，内切；(3)d>R+r,外离；（4）R-r<d<R+r,相交；
（5）d<R-r，内含；
6、例4（1）90；（2）PA=PB，∠APO=∠BPO；
7、（1）例5：π；（2）例6：①
；②36πcm2；（3）例7：20πcm2；
8、三角形的三边垂直平分线，角平分线；
二、练习
（一）填空题：1，90，270，90，45； 2，60度，120度，30度； 3，1.8； 4，4，8；5，5； 6，3； 7，7； 8，1； 9，7或1； 10，1<d<7； 11，7； 12，13； 13，7或13； 14，300π； 15，π； 16，π；
（二）1A，2B，3C，4B，5B，6C，7A，8B，9B，10C
（三）解答题
1、略；2、3cm； 3、∵AB=BC，∴
，∴∠ADB=∠CDB，∵∠ABD=∠ACD，∴△ABD∽△DPC；
4、40度；5、（-2，0），（8，0）；
（0，4）、（0，-4） ；6、
；
7、连结OC，证明△POC≌△POB，得∠PCO=∠
=90度，所以PD是圆O的切线；
8、证明：（1）连结OC。
∵PD切⊙O于点C，
又∵BD⊥PD，
∴OC∥BD。
∴∠1＝∠3。
又∵OC＝OB，
∴∠2＝∠3。
∴∠1＝∠2，即BC平分∠PBD。
（2）连结AC。
∵AB是⊙O的直径，
∴∠ACB＝90°。
又∵BD⊥PD，
∴∠ACB＝∠CDB＝90°
又∵∠1＝∠2，
∴△ABC∽△CBD
∴
，
∴
9、（1）OC∥ED；（2）