中考复习系列《图形的认识》
第四课时 圆
初三（ ）班 学号： 姓名：
内容提要
一、确定一个圆有两要素，一是 ，二是 ，圆心确定 、半径确定 ；
圆既是 对称图形，又是 对称图形；它的对称中心是 ，对称轴是 ，有 条对称轴。
二、在同圆或等圆中，两个圆心角、两条弧、两条弦三组量之间，如果有一组量相等，那么，它们所对应的其它量也相等。
典型题：
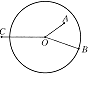
如图，AB、CD是⊙O的两条弦
①若AB=CD， 则有 = ， =
②若AB=CD， 则有 = ， =
③若∠AOB=∠COD， 则有 = ， =
三、在在同圆或等圆中，
同弧或等弧所对圆周角 ，相等的圆周角所对的弧 ，同弧或等弧所对圆周角是其所对的圆心角的 。
典型题：
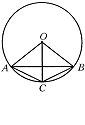
1、如图，AB、AC、BC都是⊙O的弦，∠CAB＝∠CBA，∠COB与∠COA相等吗？为什么？
 |  | ||
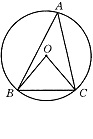2、如图，∠A是⊙O的圆周角，∠A＝30°，
则∠BOC= °，∠OBC= °
四、半圆或直径所对的圆周角都是
°，90°的圆周角所对的弦是圆是
。
典型题：
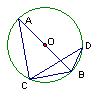
1、如图，AB是⊙O的直径，∠DCB=30°，
则∠ACD= °，∠ABD= °
2、如图，⊙O的直径AB=10，弦BC=5，
∠B= °
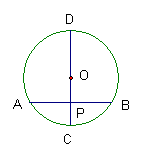五、垂直于弦的直径平分这条弦，并且平弦所对的弧。
即：如图，若AB⊥CD，
则有AP PB，AC CB，AD=
典型题：
如上图，若CD=10，AB=8，求PC的长？
六、切线
1、切线性质：圆的切线 于经过切点的半径
2、切线识别：经过半径的 （内、外）端且 于这条半径的直线是圆的切线
典型题：
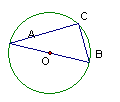
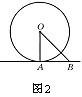
1、如图2，已知直线AB是⊙O的切线，
且AB＝OA，问∠OBA= °
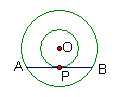2、如右图，以点O为圆心的两个同
心圆中，大圆的弦AB是小圆的切线，
点P为切点，两圆的半径分别为5cm和3cm，
则AB=
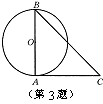
3、如图，AB是⊙O的直径，∠B＝45°，AC＝AB，AC是⊙O的切线吗？
（写出详细的过程）
七、与圆有关的位置关系
1、点与圆的位置关系 2、直线与圆的位置关系
(设⊙O半径为
，圆心到直线
距离为
)
A点在圆 
OA r
①与⊙O相交 r
B点在圆 OB r
②与⊙O相切 r
C点在圆 OC r
③与⊙O相离 r
3、圆与圆的位置关系
（1）用公共点的个数来区分
1、两个圆没有公共点， 那么就说这两个圆 ，如图3的
2、两个圆有一个公共点，那么就说这两个圆 ，如图3的
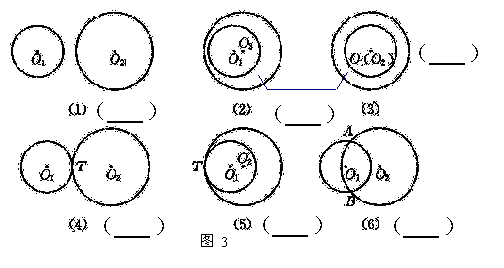3、两个圆有两个公共点，那么就说这两个圆 ，如图3的
（2）用数量关系来区别：设两圆的半径分别为
、
，圆心距为：
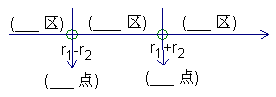
1、用数轴表示圆与圆的位置与圆心距d之间的对应关系
（在数轴上填出圆心距d各在区域中对应圆与圆的位置名称）
 |
2、根据数轴填表
| 两圆的位置关系 | 数量关系及其识别方法 |
| 外 离 | |
| 外 切 | |
| 相 交 | |
| 内 切 | |
| 内 含 |
典型题：
1、已知⊙O的半径为6，A为线段PO的中点，当OP=10时，点A与⊙O的位置关系为（ ）
A．在圆上 B．在圆外 C．在圆内 D．不确定
2、圆最长弦为12
，如果直线与圆相交，且直线与圆心的距离为，那么（ ）
A． 
B．
C．
D．
3、已知圆⊙O1和⊙O2的半径的6cm和8cm，当O1O2=12cm时, ⊙O1和⊙O2的位置关系为（ ）
A．外切 B．相交 C． 内切 D．内含
4、两圆半径和为24cm，半径之比为1：2，圆心距为8cm，则两圆的位置关系为（ ）
A．外离 B．相交 C． 内切 D．外切
八、切线长定理：
从圆 一点可以引圆的 条切线，它们的切线长 ．这一点和圆心的连线 这两条切线的 角．即：如右图， PA，PB分别为⊙O的切线，
切点分别为A、B，则PA PB， PO平分∠
典型题：
1、如下图，PA，PB分别为⊙O的切线，切点分别为A、B，∠P=60°PA=10cm，那么AB的长为
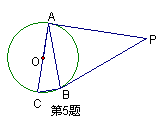
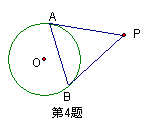2、如图，PA，PB分别为⊙O的切线，AC为直径，切点分别为A、B，∠P=70°，则∠C=
3、如上图， PA，PB分别为⊙O的切线，切点分别为A、B，PA=10，在劣弧AB上任取一点C，过C作⊙O的切线，分别交PA，PB于D，E，则△PDE的周长是
九、圆有关的计算
（1）弧长的计算
如果弧长为l，圆心角度数为n，圆的半径为r，那么，弧长
| 半径r | 圆心角度数n | 弧长l |
| 10 | 36° | |
| 5 | 2 | |
| 120° | 12 |
（圆周率用
表示即可）
（2）扇形面积计算：
方法一：如果已知扇形圆心角为n，半径为r，那么，扇形面积
方法二：如果已知扇形弧长为l，半径为r， 那么， 扇形面积
| 半径r | 圆心角度数n | 弧长l | 扇形面积 |
| 10 | 36° | ||
| 6 | 6 | ||
| 2 | 6 | ||
|
| 4 |
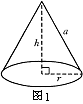
（3）圆锥的侧面积与表面积
1、如图1：
为圆锥的为 ，
为圆锥的为 ，为圆锥的底面为 ，
由勾股定理可得：、、之间的关系为：
2、如图2：圆锥的侧面展开后一个 ：圆锥的母线是扇形的
而扇形的弧长恰好是圆锥底面的 。
故：
圆锥的侧面积就是圆锥的侧面展开后的扇形的
圆锥的表面积= +
3、看图1、填表：
|
|
|
| 底面积 | 底面圆的周长 | 侧面积 | 表（全）面积 |
| 3 | 5 | |||||
| 5 | 13 | |||||
| 6 | 8 |
（圆周率用表示即可）