中考数学圆试题分类汇编(含答案)
一、选择题
1、(2007山东淄博)一个圆锥的高为3![]() ,侧面展开图是半圆,则圆锥的侧面积是( )B
,侧面展开图是半圆,则圆锥的侧面积是( )B
 (A)9
(A)9![]() (B)18
(B)18![]()
(C)27![]() (D)39
(D)39![]()
2、(2007四川内江)如图(5),这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中![]() 为
为![]() ,
,![]() 长为8cm,
长为8cm,![]() 长为12cm,则阴影部分的面积为( )
长为12cm,则阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
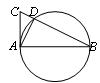 解:S=
解:S=![]() -
-![]() =
=![]() 选(B)。
选(B)。
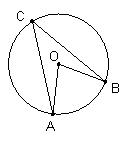
3、(2007山东临沂)如图,在△ABC中,AB=2,AC=1,以AB为直径的圆与AC相切,与边BC交于点D,则AD的长为( )。A
 A、
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、(2007浙江温州)如图,已知![]() 是
是![]() 的圆周角,
的圆周角,![]() ,则圆心角
,则圆心角![]() 是( )D
是( )D
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5、(2007重庆市)已知⊙O1的半径![]() 为3cm,⊙O2的半径R为4cm,两圆的圆心距O1O2为1cm,则这两圆的位置关系是( )C
为3cm,⊙O2的半径R为4cm,两圆的圆心距O1O2为1cm,则这两圆的位置关系是( )C
(A)相交 (B)内含 (C)内切 (D)外切
6、(2007山东青岛)⊙O的半径是6,点O到直线a的距离为5,则直线a与⊙O的位置关系为( ).C
 A.相离 B.相切 C.相交 D.内含
A.相离 B.相切 C.相交 D.内含
7、(2007浙江金华)如图,点![]() 都在
都在![]() 上,若
上,若![]() ,则
,则![]() 的度数为( )D
的度数为( )D
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、(2007山东济宁)已知圆锥的底面半径为1cm,母线长为3cm,则其全面积为( )。C
 A、π B、3π C、4π D、7π
A、π B、3π C、4π D、7π
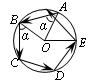
9、(2007山东济宁)如图所示,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走。按照这种方式,小华第五次走到场地边缘时处于弧AB上,此时∠AOE=56°,则α的度数是( )。A
A、52° B、60° C、72° D、76°
 10、(2007福建福州)如图2,
10、(2007福建福州)如图2,![]() 中,弦
中,弦![]() 的长为
的长为![]() cm,圆心
cm,圆心![]() 到
到![]() 的距离为4cm,则
的距离为4cm,则![]() 的半径长为( )
的半径长为( )
A.3cm B.4cm C.5cm D.6cm
C
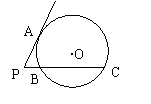 11、(2007双柏县)如图,已知PA是⊙O的切线,A为切点,PC与⊙O相交于B、C两点,PB=2 cm,BC=8 cm,则PA的长等于( )
11、(2007双柏县)如图,已知PA是⊙O的切线,A为切点,PC与⊙O相交于B、C两点,PB=2 cm,BC=8 cm,则PA的长等于( )
A.4 cm B.16 cm
 C.20 cm D.
C.20 cm D.![]() cm
cm
D
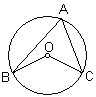
12、(2007浙江义乌)如图,已知圆心角∠BOC=100°、则圆周角∠BAC的大小是( )
A.50° B.100° C.130° D.200°
A
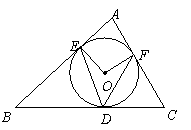 13、(2007四川成都)如图,
13、(2007四川成都)如图,![]() 内切于
内切于![]() ,切点分别为
,切点分别为![]() .
.
已知![]() ,
,![]() ,连结
,连结![]() ,
,
那么![]() 等于( )
等于( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
B
 二、填空题
二、填空题
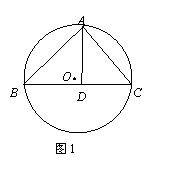
1、(2007山东淄博)如图1,已知:△ABC是⊙O的内接三角形,
AD⊥BC于D点,且AC=5,DC=3,AB=![]() ,
,
则⊙O的直径等于 。
![]()
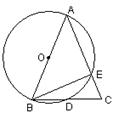
2、(2007重庆市)已知,如图:AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=450。给出以下五个结论:①∠EBC=22.50,;②BD=DC;③AE=2EC;④劣弧![]() 是劣弧
是劣弧![]() 的2倍;⑤AE=BC。其中正确结论的序号是
。①②④;
的2倍;⑤AE=BC。其中正确结论的序号是
。①②④;
 3、(2007浙江金华)如图所示为一弯形管道,其中心线是一段圆弧
3、(2007浙江金华)如图所示为一弯形管道,其中心线是一段圆弧![]() .已知半径
.已知半径![]() ,
,![]() ,则管道的长度(即
,则管道的长度(即![]() 的长)为
cm.(结果保留
的长)为
cm.(结果保留![]() )
)
![]()
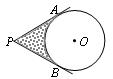
4、(2007山东济宁)如图,从P点引⊙O的两切线PA、PA、PB,A、B为切点,已知⊙O的半径为2,∠P=60°,则图中阴影部分的面积为 。
 4
4![]() -
-![]()
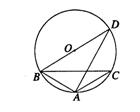
 5、(2007山东枣庄)如图,△ABC内接于⊙O,∠BAC=120°,
5、(2007山东枣庄)如图,△ABC内接于⊙O,∠BAC=120°,
AB=AC,BD为 ⊙O的直径,AD=6,则BC= 。
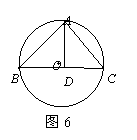
6、(2007双柏县)如图6,⊙O是等边三角形ABC的外接圆,
点D是⊙O上一点,则∠BDC = .
 60°
60°
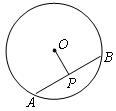
7、(2007福建晋江)如图,点P是半径为5的⊙O内的一点,且OP=3,设AB是过点P的⊙O内的弦,且AB⊥OP,则弦AB长是________。
8
 8、(2007四川成都)如图,已知
8、(2007四川成都)如图,已知![]() 是
是![]() 的直径,弦
的直径,弦![]() ,
,
![]() ,
,![]() ,那么
,那么![]() 的值是
的值是
.
![]()
三、解答题
1、(2007浙江温州)如图,点P在![]() 的直径BA的延长线上,AB=2PA,PC切
的直径BA的延长线上,AB=2PA,PC切![]() 于点C,连结BC。
于点C,连结BC。
(1)求![]() 的正弦值;
的正弦值;
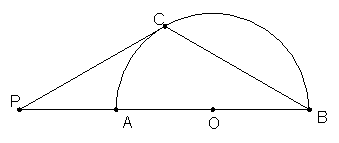 (2)若
(2)若![]() 的半径r=2cm,求BC的长度。
的半径r=2cm,求BC的长度。
解:(1)连结OC,因为PC切![]() 于点C,
于点C,![]()
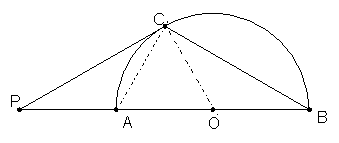
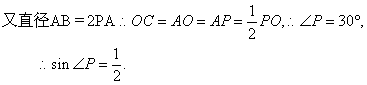
(或:在![]() )
)
(2)连结AC,由AB是直![]()
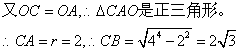
2、(2007浙江金华)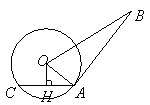 如图,
如图,![]() 是
是![]() 的切线,
的切线,![]() 为切点,
为切点,![]() 是
是![]() 的弦,过
的弦,过![]() 作
作![]() 于点
于点![]() .若
.若![]() ,
,![]() ,
,![]() .
.
求:(1)![]() 的半径;
的半径;
(2)![]() 的值;
的值;
(3)弦![]() 的长(结果保留两个有效数字).
的长(结果保留两个有效数字).
解:(1)![]()
![]() 是
是![]() 的切线,
的切线,![]()
![]() ,
,
![]() ,
,![]() .
.
(2)![]() ,
,![]() ,
,![]() .
.
(3)![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
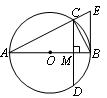
3、(2007山东济宁)如图,AB为⊙O的直径,弦CD⊥AB于点M,过点B作BE∥CD,交AC的延长线于点E,连结BC。
(1)求证:BE为⊙O的切线;
(2)如果CD=6,tan∠BCD=![]() ,求⊙O的直径。
,求⊙O的直径。

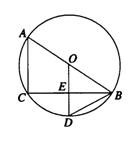 4、(2007山东枣庄)如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交
4、(2007山东枣庄)如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交![]() 于D.
于D.
(1)请写出五个不同类型的正确结论;
(2)若BC=8,ED=2,求⊙O的半径.
解:(1)不同类型的正确结论有:
①BC=CE ;②![]() = ③∠BED=90°④∠BOD=∠A;⑤AC∥OD,⑥AC⊥BC;
= ③∠BED=90°④∠BOD=∠A;⑤AC∥OD,⑥AC⊥BC;
⑦OE2+BE2=OB2;⑧S△ABC=BC·OE;⑨△BOD是等腰三角形,⑩△BOE∽△BAC;等
(2)∵OD⊥BC, ∴BE=CE=![]() BC=4.
BC=4.
设⊙O的半径为R,则OE=OD-DE=R-2.
在Rt△OEB中,由勾股定理得 OE2+BE2=OB2,即(R-2)2+42=R2.
解得R=5.∴⊙O的半径为5.
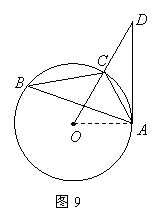
5、(2007福建福州)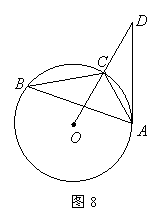 如图8,已知:
如图8,已知:![]() 内接于
内接于![]() ,点
,点![]() 在
在![]() 的延长线上,
的延长线上,![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的长.
的长.
(1)证明:如图9,连结![]() .
.
![]() ,
,![]() .
.
![]() ,
,![]() .
.
![]() ,
,![]() .
.
![]() 是
是![]() 的切线.
的切线.
(2)解:![]() ,
,![]() .
.
![]() 是等边三角形,
是等边三角形,![]() .
.
![]() ,
,![]() ,
,![]() .
.
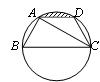 6、(2007山东临沂)如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10。
6、(2007山东临沂)如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10。
(1)求此圆的半径;
(2)求图中阴影部分的面积。

 7、(2007山东德州)如图12,
7、(2007山东德州)如图12,![]() 是
是![]() 的内接三角形,
的内接三角形,![]() ,
,![]() 为
为![]() 中
中![]() 上一点,延长
上一点,延长![]() 至点
至点![]() ,使
,使![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求证:
,求证:![]() .
.
证明:(1)在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() .
.
![]() ,(同弧上的圆周角相等),
,(同弧上的圆周角相等),![]() .
.
![]() .
.![]() .
.
在![]() 和
和![]() 中,
中,
![]()
![]() .
.![]() .
.
(2)若![]() .
.
![]() .
.
![]() ,又
,又![]()
![]()
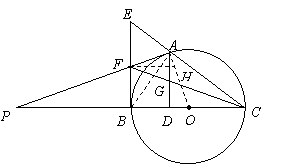
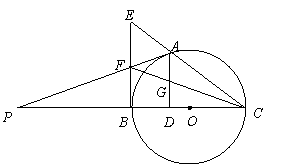 8、(2007四川成都)如图,
8、(2007四川成都)如图,![]() 是以
是以![]() 为直径的
为直径的![]() 上一点,
上一点,![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线,与
的切线,与![]() 的延长线相交于点
的延长线相交于点![]() 是
是![]() 的中点,连结
的中点,连结![]() 并延长与
并延长与![]() 相交于点
相交于点![]() ,延长
,延长![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() 是
是![]() 的切线;
的切线;
(3)若![]() ,且
,且![]() 的半径长为
的半径长为![]() ,求
,求![]() 和
和![]() 的长度.
的长度.
(1)证明:![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的切线,
的切线,
![]() .
.
又![]() ,
,![]() .
.
易证![]() ,
,![]() .
.
![]() .
.![]() .
.
![]() 是
是![]() 的中点,
的中点,![]() .
.![]() .
.
(2)证明:连结![]() .
.
![]() 是
是![]() 的直径,
的直径,![]() .
.
在![]() 中,由(1),知
中,由(1),知![]() 是斜边
是斜边![]() 的中点,
的中点,
![]() .
.![]() .
.
又![]() ,
,![]() .
.
![]() 是
是![]() 的切线,
的切线,![]() .
.
![]() ,
,![]() 是
是![]() 的切线.
的切线.
(3)解:过点![]() 作
作![]() 于点
于点![]() .
.![]() ,
,![]() .
.
由(1),知![]() ,
,![]() .
.
由已知,有![]() ,
,![]() ,即
,即![]() 是等腰三角形.
是等腰三角形.
![]() ,
,![]() .
.![]() ,
,![]() ,即
,即![]() .
.
![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,![]() .
.
![]() ,易证
,易证![]() .
.
![]() ,即
,即![]() .
.
![]() 的半径长为
的半径长为![]() ,
,![]() .
.
![]() .解得
.解得![]() .
.![]() .
.
![]() ,
,![]() .
.![]() .
.
在![]() 中,
中,![]() ,
,![]() ,由勾股定理,得
,由勾股定理,得![]() .
.
![]() .解得
.解得![]() (负值舍去).
(负值舍去).![]() .
.
[或取![]() 的中点
的中点![]() ,连结
,连结![]() ,则
,则![]() .易证
.易证![]() ,
,
![]() ,故
,故![]() ,
,![]() .
.
由![]() ,易知
,易知![]() ,
,![]() .
.
由![]() ,解得
,解得![]() .
.
又在![]() 中,由勾股定理,得
中,由勾股定理,得![]() ,
,![]() (舍去负值).]
(舍去负值).]