应用类专题单元测试题
（满分：100分；考试时间：100分钟）
| 题号 | 一 | 二 | 三 | 总分 | ||||||
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | ||||
| 得分 | ||||||||||
一、填空题（每小题3分，共21分）
1. 一件文具标价为a元，现按标价的7折出售，则售价用代数式表示为 。
2. 一项工程，甲独做需12小时完成，若甲、乙合做需4小时完成，则乙独做需 小时完成。
3. 已知某校九年级共有学生785人，其中男生人数y比女生人数x多15人，则列出的方程组为 。
4. 小明用100元钱去购买笔记本和钢笔共30件，已知每本笔记本2元，每支钢笔5元，则小明最多能买 支钢笔。
5. 学校有若干个房间分配给九年级（三）班的男生住宿，已知该班男生不足50人，若每间住4人，则余15人无住处；若每间住6人，则恰有一间不空也不满（其余均住满），那么该班男生人数是 人。
6. 一化工厂生产某种产品，产品出厂价为500元/吨，其原材料成本（含设备损耗）为200元/吨，同时，生产1吨该产品需付环保处理费及各项支出共计100元，写出利润y（元）与产品销售x（吨）之间的函数关系式 ，销售该产品 吨，才能获得10万元利润。
7. 汽车刹车距离S（m）与速度V（km/h）之间的函数关系是S=
V2 ，在一辆车速为100km/h的汽车前方80m处发现停放一辆故障车，此时刹车 有危险。（填“会”或“不会”）
二、选择题：（每小题3分，共18分）
8. 随着通讯市场竞争日异激烈，某通讯公司的手机市话收费标准按原计划的标准每分钟降价了a元后，再次下调了25%，现在的收费标准是每分钟b元，则原收费标准每分钟为（ ）
A. (
b-a)元 B. (b+a)元 C. (
b+a)元 D. (
b+a)元
9. 某种商品的进价为800元，出售时的标价为1200元，后来由于该商品积压，商店准备打折出售，但要保持利润率不低于5%，则至少可打（ ）
A. 6折 B. 7折 C. 8折 D. 9折
10. 一个两位数，个位数字比十位数字大2，并且它大于20小于50，它是（ ）
A. 24 B. 35 C. 46 D. 以上都是
11. A、B两地相距450千米，甲、乙两车分别从A、B两地同时出发，相向而行，已知甲车的速度是120千米/时，乙车的速度为80千米/时，经过t（小时）两车相距50千米，则t的值是（ ）
A. 2或2.5 B. 2或0 C. 10或12.5 D. 2或12.5
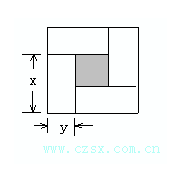12. 如图，是用4个相同的小矩形与一个小正方形镶嵌而成的正方形图案，已知该图案的面积为49，小正方形的面积为4，若用x、y表示小矩形的两边长（x＞y），请观察图案，指出以下关系中不正确的是（
）
A. x+y=7 B. x-y=2
C. 4xy+4=49 D. x2+y2=25
13. 小明在今年校运会上取得跳运冠军，函数h=3.5t-4.9t2可以描述他夺冠一跳时他跳跃的重心高度的变化（t的单位：s；h的单位：m），则他起跳后到重心最高时所用的时间大约是（ ）
A. 0.71s B. 0.63s C. 0.36s D. 0.24s
三、解答题：（共61分）
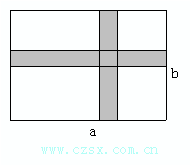
14. 如图，在长为am、宽为bm的矩形地面上，修筑两条宽都是cm且相互垂直的道路。
（1）求余下部分的面积（4分）
（2）设a=100m，b=60m，c=1m，求余下部分的面积（4分）
15. 我校篮球队参加全市中学生篮球比赛，共赛16场，共获28分。按赛制规定每赢一场得2分，输一场得1分，请你求出我校篮球队输，赢各多少场？（6分）
16. 名著《一千零一夜》中有这样一段文字：有一群鸽子，其中一部分在树上欢歌，另一部分在地上觅食，树上的一只鸽子对地上觅食的鸽子说：“若从你们中飞上来一只，则树下的鸽子就是整个鸽群的
；若从树上飞下去一只，则树上树下的鸽子就一样多了”你知道树上、树下各有多少只鸽子吗？（6分）
17. 某重点高中高一年级近几年来招生人数逐年增加，去年达到550名，其中有统招生，也有择校缴费生。由于场地、师资等限制，今年招生最多比去年增加100人，其中统招生可多招20%，择校生可多招10%，问今年最多可多招收统招生多少人？（6分）
18. 某工厂生产某种产品，每件产品的出厂价为100元,其成本价为50元，因为在生产过程中。平均每生产一件产品有0.5m3的污水排出，所以为了净化环境，工厂设计了两种方案对污水进行处理，并准备实施。（12分）
方案1：工厂污水先净化处理再排出。每处理1m3污水所用原料费为4元，并且每月排污设备损耗费为60000元。
方案2：工厂将污水排到污水厂统一处理，每处理1m3污水需付28元排污费。
（1）设工厂每月生产x件产品，每月利润为y元，分别求出依方案1和方案2处理污水时，y与x的函数关系式
（2）设工厂每月生产量为6000件时，你若作为厂长在不污染环境，又节约资金的前提下应选用哪种处理污水的方案？请你通过计算加以说明。
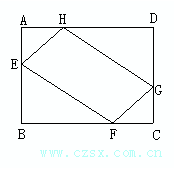
19. 为了美化环境，学校准备在一块空地上（如图矩形ABCD，其中AB=20m，BC=40m）进行绿化，中间的一块（四边形EFGH）上种花，其余的四块（四个直角三角形）上铺设草坪，并要求AE=AH=CF=CG。那么在满足上述条件的所有设计中，是否存在一种设计，使得四边形EFGH面积最大？若存在，请求出该设计中AE的长及四边形EFGH的面积；若不存在，请说明理由。（10分）
20. 光源灯具厂工人的工作时间是：每月25天，每天8小时。待遇是：按件计酬，多劳多得，每月另加福利工资100元，按月结算。该厂生产A、B两种产品，工人每生产一件A产品，可得报酬0.75元，每生产一件B产品，可得报酬1.40元，下表记录了工人小明的工作情况：
| 生产A种产品件数 | 生产B种产品件数 | 总时间（分钟） |
| 1 | 1 | 35 |
| 3 | 2 | 85 |
根据上表提供的信息，请回答下列问题：
（1）小明每生产一件A种产品，每生产一件B种产品，分别需要多少分钟？（6分）
（2）如果生产各种产品的数目没有限制，那么小明每月的工资数目在什么范围之内？（7分）
参 考 答 案
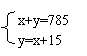一、填空题：
1. 
a 2. 6 3.
4. 13
5. 47
6. y=200x 500 7. 会
二、选择题：
8. D 9.B 10. D 11. A 12. D 13. C
三、
14. （1）可将两条相互垂直的道路平移到如图所示的位置，便于计算余下部分面积=(a-c)(b-c)=ab-ac-bc+c2
(2)当a=100，b=60，c=1时，余下面积=（100-1）（60-1）=99×59=5841（m2）
15. 设赢x场，则输（16-x）场，依照意得：
2x+(16-x)=28
解得：x=12 ∴16-x=16-12=4
答：我校篮球队赢了12场，输了4场。
16. 设树上有x只鸽子，树下有y只鸽子，则：
y-1=(x+y)
x-1=y+1
x=7
解得：
y=5
答：树上原有鸽子7只，树下有5只鸽子。
17. 设去年统招生有x人，则去年择校生有（550-x）人，则：
20%x+10%（550-x）≤100
解得 x ≤450
∴20%x ≤90
∴今年统招生最多可多招收90人。
18.（1）设选用方案1，每月利润为y1元，选用方案2，每月利润为y2元
由方案1，得y1=（100-50）x-4×0.5x-60000=48x-60000
由方案2，得y2=(100-50)x-28×0.5x=36x
（2）当x=6000时，
y1=48×6000-60000=228000（元）
y2=36×6000=216000（元）
∴y1＞y2
∴我作为厂长，应选用方案1
19. 存在满足要求的四边形EFGH，设AE=AH=CG=CF=x，则BE=DG=20-x，BF=DH=40-x
∴四边形EFGH的面积S=40×20-2×
x2-2×(20-x)(40-x)
=-2x2+60x
=-2(x-15)2+450
∵0＜15＜20，且a=-2＜0，∴S有最大值
∴当x=15时，S最大值=450（m2）
20. （1）设小明每生产1件A种产品，每生产1件B种产品分别需要a分钟和b分钟，则 a+b=35
3a+2b=85
a=15
解得：
b=20
（2）设小明每月生产x件A种产品，y件B种产品（x、y均为非负整数），月工资数目为S元，则
15x+20y=25×8×60
S=0.75x+1.40y+100
X≥0，y≥0
y=600-0.75x
即 S=-0.3x+940
0≤x≤800
在S=-0.3x+940中
∵-0.3＜0，且0≤x≤800
∴当x=0时，S最大值=940（元）
当x=800时，S最小值=-0.3×800+940=700（元）
∵生产各种产品的数目没有限制。
∴700≤S≤940
∴小明每月的工资数目不低于700元，而不高于940元。