中考数学全真模拟试题25
考生注意：１、数学试卷共8页，共24题．请您仔细核对每页试卷下方页码和题数，核实
无误后再答题．
２、请您仔细思考、认真答题，不要过于紧张，祝考试顺利！
| 题 号 | 一 | 二 | 三 | 总 分 | |||||||
| （1～10） | （11～16） | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | ||
| 得 分 | |||||||||||
| 得 分 | 评卷人 |
一、选择题：（本大题共10小题，每小题4分，共40分）
在每小题给出的四个选项中，只有一项是符合题意的，请把你认
为正确的选项前的字母填写在本答案表中．
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 |
１．芜湖地处长江中下游，水资源丰富，素有“江南水乡”之美称．据测量，仅浅层地下水
蕴藏量就达56000万m3，用科学记数法记作 （ ）
Ａ．
m3 Ｂ．
m3 Ｃ．
m3 Ｄ．
m3
２．请阅读一小段约翰
斯特劳斯作品，根据乐谱中的信息，确定最后一个音符的时值长应
为 （ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
|
３．在“手拉手，献爱心”捐款活动中，九年级七个班级的捐款数分别为：260、300、240、
220、240、280、290(单位：元)，则捐款数的中位数为 （ ）
Ａ．280 Ｂ．260 Ｃ．250 Ｄ．270
４．已知
和
的半径分别是5和4，
，则和的位置关系是（ ）
Ａ．外离 Ｂ．外切 Ｃ．相交 Ｄ．内切
５．在平面直角坐标系中，点
所在象限是 （ ）Ａ．第一象限 Ｂ．第二象限 Ｃ．第三象限 Ｄ．第四象限
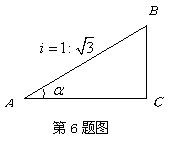
６．如图，已知一坡面的坡度
，则坡角
为 （ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
７．下列图形中，是轴对称而不是中心对称图形的是 （ ）
Ａ．平行四边形 Ｂ．菱形 Ｃ．等腰梯形 Ｄ．直角梯形
８．若使分式
的值为0，则
的取值为 （ ）
Ａ．1或
Ｂ．
或１ Ｃ． Ｄ．或
９．若一个多边形的内角和为外角和的3倍，则这个多边形为 （ ）
Ａ．八边形 Ｂ．九边形 Ｃ．十边形 Ｄ．十二边形
10．估算
的值 （ ）
Ａ．在4和5之间 Ｂ．在5和6之间 Ｃ．在6和7之间 Ｄ．在7和8之间
| 得 分 | 评卷人 |
二、填空题：（本大题共6小题，每小题5分，共30分）
11．函数
中，自变量的取值范围是 ．
12．已知等腰三角形两边长为7和3，则它的周长为 ．
13．若反比例函数
的图象经过点
，则
．
14．计算：
．
15．在珠穆朗玛峰周围2千米的范围内，还有较著名的洛子峰（海拔8516米）、卓穷峰（海
拔7589米）、马卡鲁峰（海拔8463米）、章子峰（海拔7543米）、努子峰（海拔7855
米）、和普莫里峰（海拔7145米）六座山峰，则这六座山峰海
拔高度的极差为 米．
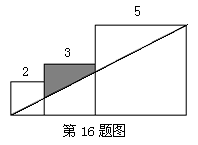
16．已知三个边长分别为2、3、5的正方形如图排列，则图中
阴影部分面积为 ．
三、解答题：本大题共8小题，共80分，解答应写明文字说明和运算步骤．
| 得 分 | 评卷人 |
17．（本题共两小题，每小题6分，满分12分）
（1）解不等式组：
（2）因式分解：
解：（1） 解：（2）
| 得 分 | 评卷人 |
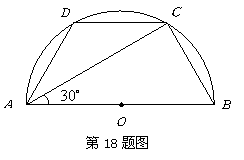
18．（本小题满分8分）
如图，已知在半圆
中，
，
，求
的长度．
解：
| 得 分 | 评卷人 |
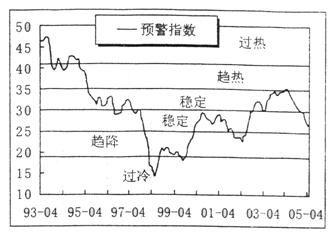
19．（本小题满分8分）
|
（1）请你仔细阅读图表，可从图表
中得出：
我国经济发展过热的最高点出现在
年；我国经济发展过冷的最低
点出现在 年．
（2）根据该图表提供的信息，请你
简单描述我国从1993年4月到2005年4
月经济发展状况，并预测2005年度中国
经济发展的总体趋势将会怎样？
答：
第19题图
| 得 分 | 评卷人 |
20．（本小题满分8分）
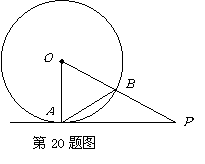如图，
为
的切线，
为切点，
交于点
，求
的度数．
解：
| 得 分 | 评卷人 |
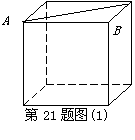
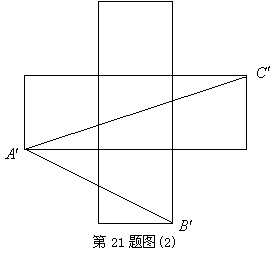
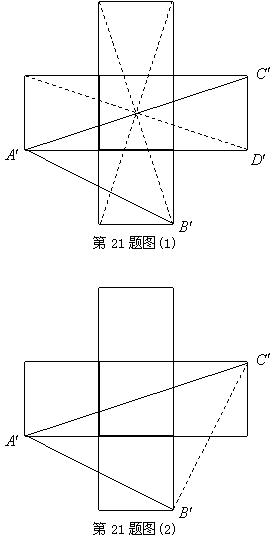
21．（本小题满分10分）
如图（1）所示为一上面无盖的正方体纸盒，现将其剪开展成平面图，如图（2）所示．
已知展开图中每个正方形的边长为1．
（1）求在该展开图中可画出最长线段的长度？这样的线段可画几条？
（2）试比较立体图中
与平面展开图中
的大小关系？
|
 |
| 得 分 | 评卷人 |
22．（本小题满分10分）
已知二次函数图象经过
，对称轴
，抛物线与轴两交点距离为4，求这个二次函数的解析式？
解：
| 得 分 | 评卷人 |
23．（本小题满分12分）
小胖和小瘦去公园玩标准的跷跷板游戏，两同学越玩越开心，小胖对小瘦说：“真可惜！
我只能将你最高翘到1米高，如果我俩各边的跷跷板都再伸长相同的一段长度，那么我
就能翘到1米25，甚至更高！”
（1）你认为小胖的话对吗？请你作图分析说明；
（2）你能否找出将小瘦翘到1米25高的方法？试说明．
解：
| 得 分 | 评卷人 |
24．（本小题满分12分）
在科技馆里，小亮看见一台名为帕斯卡三角的仪器，如图所示，当一实心小球从入口落下，它在依次碰到每层菱形挡块时，会等可能地向左或向右落下．
（1）试问小球通过第二层位置的概率是多少？
（2）请用学过的数学方法模拟试验，并具体说明小球下落到第三层
位置和第四层
位置处的概率各是多少？
解：
参考答案及评分标准
一、单项选择题（本大题共10小题，每题4分，满分40分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | C | B | C | D | C | C | C | A | D |
二、填空题（本大题共6小题，每题5分，满分30分）
11．
12．
13．
14．
15．1371 16．
三、解答题：本大题共8小题，共80分，解答应写明文字说明和运算步骤．
17．（本小题满分12分）
（1）
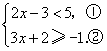
解：由①得 
．·························· 2分
由②得 
．························· 4分
不等式组解集为
．···················· 6分
（2）解：
························· 2分
．······················ 6分
18．（本小题满分8分）
解：
为直径，
，·················· 1分
····· 2分
．
．····························· 4分
在
中
且
．··········· 5分
．······················· 6分
．······························ 8分
19．（本小题满分8分）
答：（1）1993，1998．·························· 4分
（2）从1993年经济过热逐渐降温，到1998年经济过冷，之后经济逐步回升并趋于稳
定．·································· 6分
由图表预测2005年经济虽然有所降温，但总体保持稳定．·········· 8分
20．（本小题满分8分）
解：
为的切线，为切点
．······················ 2分
在
中 
········· 4分
．
在
中 
．········· 6分
．··············· 8分
21．（本小题满分10分）
解：（1）在平面展开图中可画出最长的线段长为
．
······················· 1分
如图（1）中的
，在
中
，由勾股定理得：
···· 3分
答：这样的线段可画4条（另三条用虚线标出）．· 4分
（2）
立体图中为平面等腰直角三角形的一锐角，
．··············· 5分
在平面展开图中，连接线段
，由勾股定理可得：
．··········· 7分
又
，
由勾股定理的逆定理可得
为直角三角形．
又
，
为等腰直角三角形．········· 8分
|
．·············· 9分
所以与相等．········· 10分
22．（本小题满分10分）
解：
抛物线与轴两交点距离为4，且以为对称轴．
抛物线与轴两交点的坐标为
．··············· 4分
设抛物线的解析式
．·················· 6分
又抛物线过点，
．························· 8分
解得
．······························ 9分
二次函数的解析式为
．················· 10分
23．（本小题满分12分）
解：（1）小胖的话不对．·········· 2分
小胖说“真可惜！我现在只能将你最高翘到1
米高”，情形如图（1）所示，
是标准跷跷
板支架的高度，
是跷跷板一端能翘到的最
高高度1米，
是地面．
······························ 4分
又此跷跷板是标准跷跷板，
，
而
米，得
米．················· 5分
若将两端同时都再伸长相同的长度，假设为
米
．
如图（2）所示，
米，
米····· 6分
，即
．
，同理可得
．
，由米，得
米．
······················· 7分
综上所述，跷跷板两边同时都再伸长相同的一段长度，
跷跷板能翘到的最高高度始终为支架高度的两倍，
所以不可能翘得更高．
（2）方案一：如图（3）所示，保持
长度不变．将
延长一半至
，即只将小瘦一边伸长一半．·· 8分
使
则
．·········· 9分
由
得
······ 11分
米．··············· 12分
方案二：如图（4）所示，只将支架升高0.125米．
······················· 8分
又
米．········ 9分
．··························· 11分
米．··························· 12分
（注：其它方案正确，可参照上述方案评分！）
24．（本小题满分12分）
方法1：①实心小球在碰到菱形挡块时向左或向右下落是等可能性的经过一个菱形挡块后向左或向右下落的概率各是原概率的一半．··························· 1分
画树状图可知，落到点位置的概率为
．············· 4分
②同理可画树状图得，落到点位置的概率为
．·········· 8分
③同理可画树状图得，落到点位置的概率为
．········· 12分
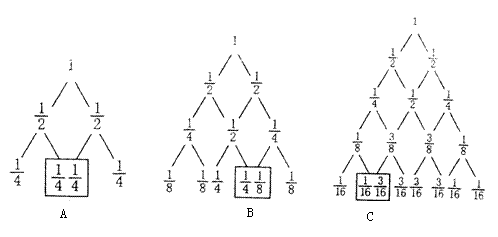（注：①中画图1分，算出概率2分．②、③中画图2分，算出概率2分．）
方法2：（1）实心小球碰到每个菱形挡块时向左或向右是等可能性的，因此小球下落到的可能性会有以下的途径｛左右，右左｝两种情况，························ 1分
而下落到第二层，共｛左左，左右，右左，右右｝四种情况·········· 2分
由概率定义得
······················· 4分
（2）同理，到达第三层位置会有以下途径｛左右右，右左右，右右左｝三种情况
···································· 5分
而下落到第三层共有｛左左左，左左右，左右左，左右右，右左左，右左右，右右左，右右右｝八种情况 6分
由概率定义得
························· 8分
（3）同理，到达第四层位置会有｛左左左右，左左右左，左右左左，右左左左｝四种情况 9分
而下落到第四层共有｛左左左左，左左左右，左左右左，左右左左，右左左左，左右左右，左右右左，左左右右，右左左右，右左右左，右右左左，右右右左，右右左右，右左右右，左右右右，右右右右｝共16情况 10分
由概率定义得
······················ 12分
方法3：本题也可用贾宪三角方法，先算出小球下落路径条数，如下图．由题意知：小球经过每条路径的可能性相同．
 |
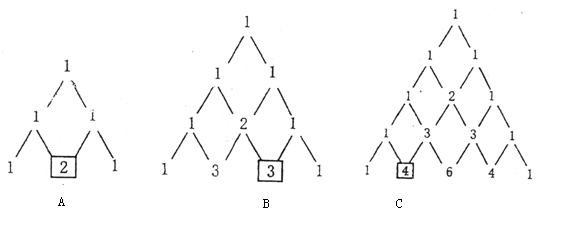由概率定义易得
，（其中画图2分，算出概率2分）·· 4分
，（其中画图2分，算出概率2分）·········· 8分
．（其中画图2分，算出概率2分）····· 12分
（注：其它方案正确，可参照上述方案评分！）