 中考数学招生模拟考试题
中考数学招生模拟考试题
| 题号 | 一 | 二 | 三 | 总分 | |||||||
| 得分 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | |||
注意事项:本试卷共8页,三大题,满分120分,考试时间100分钟。请用圆珠笔或钢笔直接答在试卷上。
| 得 分 | 评卷人 |
|
|
一、选择题:(每题3分,共18分.)下列各题的四个答案,其中只有一个是正确的,将正确答案的代号字母填入题后括号内。
1. 通过四舍五入得到的近似值3.56万精确到( )
A.万位 B.千位 C.百位 D.百分位
 2. 第48届世乒赛刚刚在上海落幕,中国队再次囊括了五个单项的金牌。在有64名选手抽签分上下两个半区后,采用单淘汰的规程,最终笑傲群雄的是我国的王励勤,那么王励勤共打了( )场比赛获得冠军。
2. 第48届世乒赛刚刚在上海落幕,中国队再次囊括了五个单项的金牌。在有64名选手抽签分上下两个半区后,采用单淘汰的规程,最终笑傲群雄的是我国的王励勤,那么王励勤共打了( )场比赛获得冠军。
A. 4 B. 5 C.6 D.7 400
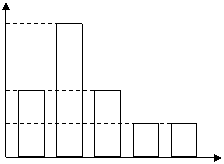
3. 如图,是王老师五月份的家庭开支条形统
计图,该条形统计图还用以( )来表示。
A.折线统计图 B.扇型统计图
C.分布直方图 D.折线或扇型统计图 200
( 注:JY指教育开支;SH指基本生活开
LY指旅游开支;SD指水电费;QT指其他 ) 100
JY SH LY SD QT
4.
下列各图中每个正方形网格都是由四个边长为1的小开放型组成,其中阴影部分面积是小正方形面积的![]() 的是 ( )
的是 ( )
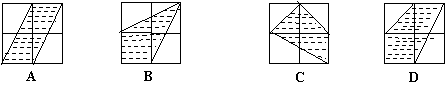 |
5.小兰和小潭分别用掷A、B两枚骰子的方法来确定P(![]() ,
,![]() )的位置,她们规定:小兰掷得的点数为
)的位置,她们规定:小兰掷得的点数为![]() ,小谭掷得的点数为
,小谭掷得的点数为![]() ,那么,她们各掷一次所确定的点落在已知直线
,那么,她们各掷一次所确定的点落在已知直线![]() 上的概率为( )
上的概率为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
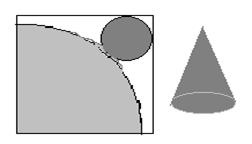
6. 在正方形铁皮上剪下个圆形和扇形,使之恰好围成如图所示的圆锥模型.设圆
的半径为r,扇形的半径为R,则圆半径与扇形半径之间的关系是 ( )
 A、2r=R B、
A、2r=R B、![]()
C、![]() D、
D、![]()
| 得 分 | 评卷人 |
|
|
二、填空题(每小题3分,共27分)
![]() 7. 已知a 在数轴上的位置如图
那么化简︱a-1︱+︱a+1︱= .
7. 已知a 在数轴上的位置如图
那么化简︱a-1︱+︱a+1︱= .
8. 小明把如图所示的4张扑克牌放在一张桌子上,请一位同学避开他任意将其中一张牌旋转倒过来.然后小明很快辨认了哪张牌被倒过来了,那么图中被倒过来的扑克牌是 ,其辨认所依据的数学知识是 .
 |
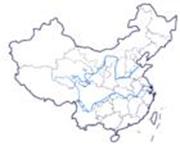
![]() 9. .海峡两岸血浓于水,近期国民党主席连战和亲 0 600千米
9. .海峡两岸血浓于水,近期国民党主席连战和亲 0 600千米
民党主席宋楚瑜分别率团访问大陆,受到大陆 北京*
人民的热情接待,右图是我国政区图,根据相
关信息,台北与北京的实际距离,<直线距离>
约是 (精确到千米)。 台北 *
10. 爸爸上个月的电话费用37.5元,其中月租费是12.5元,每打一次市话
不超过3分钟收费0.2元.爸爸上月没有打过长途或其他电话,且每次却不
超过3分钟,那么爸爸上个月累计通话时间至多为________分钟.
11. 有两组扑克牌各三张,牌面数字分别是1,2,3,随意从每组中个抽出一张。数字和是偶数的概率是 。
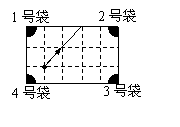 12.如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多反射),那么该球最后将落入的球袋是
12.如图是一个经过改造的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多反射),那么该球最后将落入的球袋是
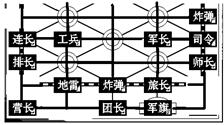
13. 如图,在一次军棋比赛中,如果团长所在的位置的坐标为(2,-5),司令所在的位置的坐标为(4,-2),那么工兵所在的位置的坐标为 ;
14. 给出下列函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 。
。
其中,![]() 随
随![]() 的增大而减小的函数是
的增大而减小的函数是
15. 扑克牌游戏
小明背对小亮,让小亮按下列四个步骤操作:
第一步 分发左、中、右三堆牌,每堆牌不少于两张,且各堆牌现有的张数相同;
第二步 从左边一堆拿出两张,放入中间一堆;
第三步 从右边一堆拿出一张,放入中间一堆;
第四步 左边一堆有几张牌,就从中间一堆拿几张牌放入左边一堆.
这时,小明准确说出了中间一堆牌现有的张数.你认为中间一堆牌现有的张数是 .
三、解答题:(本大题有8小题,满分 75分)
| 得分 | 评卷人 |
|
|
16.(8分)老师布置了一道计算题:计算![]() 的值,其中
的值,其中![]() ,小明把
,小明把![]() 错抄成
错抄成![]() ,但老师发现他的答案还是正确的,你认为这是怎么回事?说说你的理由;
,但老师发现他的答案还是正确的,你认为这是怎么回事?说说你的理由;
| 得分 | 评卷人 |
|
|
17.(9分) 现代营养学家用身体质量指数判断人体的健康状况,这个指数等于人体质量(千克)与人体身高(米)平方的商,一个健康人的身体质量指数在20~25之间,身体质量指数低于18,属于不健康的瘦;身体质量指数高于30,属于不健康的胖。(1)根据以上信息,请你判断是否存在着某两个变量之间有函数关系?若存在,写出它们的函数表达式。若没有,说明理由;(2)A同志的体重为90千克,身高为1.6米,A属于哪种类型的人?(3)B同志的体重在65~70之间,经测定,该同志的身体质量指数为23,请估算该同志的身高.
| 得分 | 评卷人 |
|
|
18. (9分) 下面两幅统计图(如图1、图2),反映了某市甲、乙两所中学学生参加课外活动的情况.请你通过图中信息回答下面的问题.
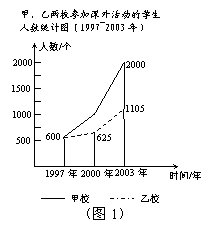
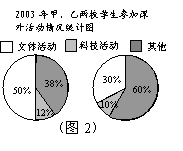
(1)通过对图1的分析,写出一条你认为正确的结论;(3分)
(2)通过对图2的分析,写出一条你认为正确的结论;(3分)
(3)2003年甲、乙两所中学参加科技活动的学生人数共有多少?(3分)
| 得分 | 评卷人 |
|
|
19(9分) 如图,⊙O的直径为AB,过半径OA的中点G作弦CE⊥AB,在弧CB上取一点D,分别作直线CD,ED交直线AB于F,M,连结OC,MC.
(1)
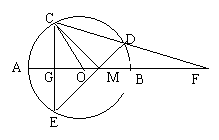 求∠AOC和∠MDF的度数;
求∠AOC和∠MDF的度数;
(2)求证:△MDF∽△MOC.
| 得分 | 评卷人 |
|
|
20. (9分)
如图,等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD,过
D点作DE∥AC交BC的延长线于E点。
⑴求证:四边形ACED是平行四边形;(4分)
 ⑵若AD=3,BC=7,求梯形ABCD的面积;(5分)
⑵若AD=3,BC=7,求梯形ABCD的面积;(5分)
| 得分 | 评卷人 |
|
|
21.(10分)如图1是某段河床横断面的示意图.查阅该
河段的水文资料,得到下表中的数据:
| x/m | 5 | 10 | 20 | 30 | 40 | 50 |
| y/m | 0.125 | 0.5 | 2 |
| 8 | 12.5 |
(1) 请你以上表中的各对数据(x,y)作为
(2) 点的坐标,尝试在图2所示的坐标系中
(3) 画出y关于x的函数图象;
①填写下表:
| x | 5 | 10 | 20 | 30 | 40 |
|
|
|
②根据所填表中数据呈现的规律,猜想出用x表示y
的二次函数的表达式: .
(4) 当水面宽度为36米时,一艘吃水深度(船底部
到水面的距离)为1.8米的货船能否在这个河段安全
通过?为什么?
| 得分 | 评卷人 |
|
|
22. (10分)某校研究性学习小组在研究相似图形时,发现相似三角形的定义、判定及其性质,可以拓展到扇形的相似中去。例如,可以定义:“圆心角相等且半径和弧长对应成比例的两个扇形叫做相似扇形”;相似扇形有性质:弧长比等于半径比、面积比等于半径比的平方…。请你协助他们探索这个问题。
(1)写出判定扇形相似的一种方法:若_____________________________,则两个扇形相似;
(2)有两个圆心角相等的扇形,其中一个半径为a、弧长为m,另一个半径为2a,则它的弧长为_________________;
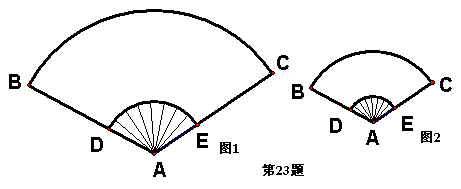
(3)如图1是一完全打开的纸扇,外侧两竹条AB和AC的夹角为120°,AB为30cm,现要做一个和它形状相同、面积是它一半的纸扇(如图2),求新做纸扇(扇形)的圆心角和半径。
| 得分 | 评卷人 |
|
|
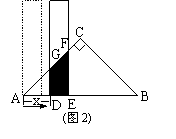
23.( 11分)有一根直尺的短边长2㎝,长边长10㎝,还有一块锐角为45°的直角三角形纸板,它的斜边长12cm..如图1,将直尺的短边DE放置与直角三角形纸板的斜边AB重合,且点D与点A重合.将直尺沿AB方向平移(如图2),设平移的长度为xcm(0≤x≤10),直尺和三角形纸板的重叠部分(图中阴影部分)的面积为S㎝2.
(1)当x=0时(如图1),S=_____________;当x = 10时,S =______________.
(2) 当0<x≤4时(如图2),求S关于x的函数关系式;

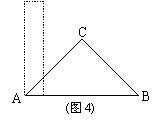
 (3)当4<x<10时,求S关于x的函数关系式,并求出S的最大值(同学可在图3、图4中画草图).
(3)当4<x<10时,求S关于x的函数关系式,并求出S的最大值(同学可在图3、图4中画草图).

 4.5
4.5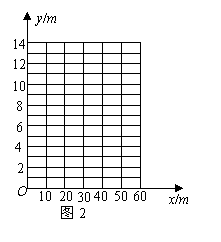 50
50