一元二次方程应用题训练
1.将进货单价为40元的商品按50元售出时，就能卖出500个.已知这种商品每个涨价1元，其销售量就减少10个，问为了赚得8000元的利润，售价应定为多少？这时应进货多少个？
解：设商品的单价是
元，则每个商品的利润是
元，销售量是
个.由题意列方程为
整理，得 
.
解方程，得 
.
故商品的的单价可定为50+10=60元或50+30=80元.
当商品每个单价为60元时，其进货量只能是500-10×10=400个，当商品每个单价为80元时，其进货量只能是 500-10×30=200个.
答：售价定为60元时，进货是400个，售价定为80元时，进货是200个
2. 某电脑公司2000年的各项经营收入中，经营电脑配件的收入为600万元，占全年经营总收入的40%，该公司预计2002年经营总收入要达到2160万元，且计划从2000年到2002年，每年经营总收入的年增长率相同，问2001年预计经营总收入为多少万元？
解：设2001年预计经营总收入为
万元，每年经营总收入的年增长率为
.
根据题意，得
解方程，得
不合题意，舍去），
∴
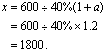
答：2001年预计经营总收入为1800万元.
3. 某市供电公司规定，本公司职工，每户一个月用电量若不超过
千瓦·时，则一个月的电费只要交10元，若超过千瓦·时，则除了交10元外，超过部分每千瓦/时还要交
元.一户职工三月份用电80千瓦·时，交电费25元；四月份用电5千瓦·时，交电费10元，试求的值.
解：由题意，可知≥45.
且有 
.
解得 
（千瓦·时），
（不合题意，舍去）.
答：的值为50千瓦·时.
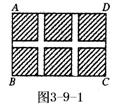4.如图3-9-1所示,某小区规划在一个长为40米,宽为26米的矩形场地
上修建三条同样宽的甬路,使其中两条与
平行,另一条与垂直,其余部分种草,若使每一块草坪的面积都为144米2,求甬路的宽度?
解:可设甬路宽为米,依题意,得
,
解得
(不合题意,舍去).
答:甬路的宽度为2米.
5. 如图3-9-2所示要建一个面积为150m2的长方形养鸡场,为了节约材料,鸡场的一边靠着原有的一条墙,墙长为m,另三边用竹篱笆围成,已知篱笆总长为35m.
(1)求鸡场的长与宽各为多少米?
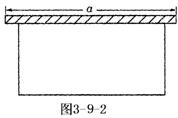(2)题中的墙长度m对题目的解起着怎样的作用?
解：（1）设鸡场的宽为
m，则长为
m.依题意列方程为 
.
整理，得 
.
解方程，得
.
所以当
时，
.
答：当鸡场的宽为10m时，长为15m；当鸡场宽为7.5m时，长为20m.
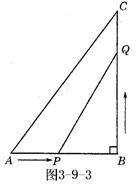
6. 已知：如图3-9-3所示，在△
中，
.点
从点开始沿边向点
以1cm/s的速度移动，点
从点开始沿
边向点
以2cm/s的速度移动.
（1）如果
分别从
同时出发，那么几秒后，△
的面积等于4cm2？
（2）如果分别从同时出发，那么几秒后，
的长度等于5cm？
（3）在（1）中，△
的面积能否等于7cm2?说明理由.
解 （1）设s后，△的面积等于4cm2，此时，
，
.
由
得
.
整理，得 
.
解方程，得 
.
当
时，
,说明此时点越过点，不合要求.
答：1s后，△的面积等于4cm2.
（2）仿（1），由
得
.
整理，得 
解方程，得
（不合，舍去），
.
答：2s后， 的长度等于5cm.
（3）仿（1），得
整理，得 
容易判断此方程无解.
答：△的面积不可能等于7cm2.