《一元二次方程》提高测试
一 填空题（本题20分，每小题4分）：
1．方程4x2＋（k＋1）x＋1＝0的一个根是2，那么k＝ ，另一根是 ；
2．方程 kx2＋1 ＝ x－x 2 无实数根，则k ；
3．如果 x2 －2（m＋1）x＋m2＋5 是一个完全平方式，则m ＝ ；
4．若方程 x2＋mx－15 ＝ 0 的两根之差的绝对值是8，则m ＝ ；
5．若方程 x2－x＋p ＝ 0 的两根之比为3，则 p＝ .
答案：
1．
，
；
2．＞
；
3．２；
4．
；
5．
．
二 选择题（本题24分，每小题4分）：
1．若一元二次方程 2x（kx－4）－x2＋6 ＝ 0 无实数根，则k的最小整数值是……（ ）
（A）－1 （B）2 （C）3 （D）4
2．若c为实数，方程x2－3x＋c＝0的一个根的相反数是方程x2＋3x－3＝0的一个根，那么方程x2 －3x＋c＝0的根是…………………………………………………………（ ）
（A）1，2 （B）－1，－2 （C）0，3 （D）0，－3
3．方程x2－3x－2＝0的最小一根的负倒数是…………………………………………（ ）
（A）－1 （B）
（C）
（3－
） （D）
4．对于任意的实数x，代数式x2－5x＋10的值是一个…………………………………（ ）
（A）非负数 （B）正数 （C）整数 （D）不能确定的数
5．若一元二次方程ax2＋bx＋c ＝ 0 （a≠0） 的两根之比为2：3，那么a、b、c间的关
系应当是………………………………………………………………………………… （ ）
（A）3b2＝8ac （B）
（C）6b2＝25ac （D）不能确定
6．已知方程3x2＋2x－6 ＝ 0 ，以它的两根的负倒数为根的新方程应是……………（ ）
（A）6x2－2x＋1＝0 （B）6x2＋2x＋3＝0 （C）6x2＋2x＋1＝0 （D）6x2＋2x－3＝0
答案：
１．Ｂ；２．Ｃ；３．Ｂ；４．Ｂ；５．Ｃ；６．Ｄ．
三 解下列方程（本题24分，每小题6分）：
1．
；
2．
；
3．4x2＋19x－5＝0；
4．
.
答案：
（1） x1＝
，x2＝－；
（2） x＝－２；
（3） x1＝
，x2＝
；
（4） x1＝
，x2＝
．
四（本题10分）
若方程2x2－3x－1＝0的两根为x1和x2，不解方程求x41＋x42的值；
答案：
．
解：因为方程2x2－3x－1＝0的两根为x1和x2，
由根与系数的关系知
，
．
所以
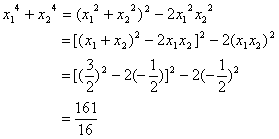
五（本题10分）
两列火车分别从A、B两站同时发出，相向而行，第一列车的速度比第二列车每小时快10 km，两车在距A、B中点28 km处相遇，若第一列车比原来晚发出45分，则两车恰在A、B中点相遇，求A、B距离及两车的速度．
答案：A、B距离为840km，第一列车速度为80km／h，第二列车速度为70km／h.
解：设A、B两站相距为2S km，第一列车速度为（x＋10）km/h，第二列车速度为xkm/h．
依题意，得
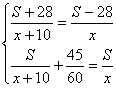
解得 
所以 A、B两站相距为840km，第一列车速度为80km／h，第二列车速度为70km／h.
六（本题12分）
挖土机原计划在若干小时挖土220m3，最初3小时按计划进行，以后每小时多挖10m3，因此提前2小时超额20m3完成任务，问原计划每小时应挖土多少m3 ？
答案：原计划每小时挖土20m3．
解：设原计划每小时挖土x m3．
依题意，得
解得 
．
所以原计划每小时挖土20m3．