初三毕业考试数学试卷
（命题：郎绍波）
（全卷三个大题，共23个小题；考试时间120分钟；满分：120分）
| 题 号 | 一 | 二 | 三 | 总 分 |
| 得 分 |
| 得分 | 评卷人 |
|
|
|
一、填空题（本大题共6个小题，每小题3分，满分18分）
1．计算：(－2)2= ．
2．一种细菌的半径是0.000039 m，用科学记数法表示这个数是 m．
3．函数y=
中自变量x的取值范围是 ．
4．点P(3，－2)关于x轴对称的点的坐标是 ．
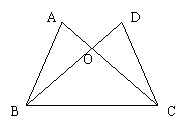
5．如图，已知AC=DB，再添加一个适当的条件
，使△ABC≌△DCB．
（只需填写满足要求的一个条件即可）
6．观察下列排列的等式：
1×2－1=12，2×3－2=22，3×4－3=32，4×5－4=42，……．
猜想：第n个等式（n为正整数）应为 ．
| 得分 | 评卷人 |
|
|
|
二、选择题（本大题共8个小题，每小题只有一个正确选项，每小题4分，满分32分）
7．下列运算正确的是( )
(A)a2a3=a6 (B)(a2)3=a6 (C)a6÷a2=a3 (D)a6-a2=a4
8．下列图形中，是中心对称图形但不是轴对称图形的是( )
(A)等边三角形 (B)平行四边形 (C)等腰梯形 (D)圆
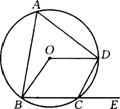9．如图，四边形ABCD内接于⊙O，如果它的一个外角
∠DCE=64°，那么∠BOD=( )
(A)128° (B)100° (C)64° (D)32°
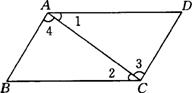10．如图，∠1=∠2，则下列结论一定成立的是（ ）
(A) AB∥CD (B) AD∥BC
(C) ∠B=∠D (D) ∠3=∠4
11．把a3－ab2分解因式的正确结果是（ ）
(A)(a+ab)(a－ab) (B)a(a2－b2)
(C)a(a+b)(a－b) (D)a(a－b)2
12．对于函数y=
，下列判断正确的是( )
(A)图象经过点(－1，3) (B)图象在第二、四象限
(C)图象所在的每个象限内，y随x的增大而减小
(D)不论x为何值时，总有y>0
13．如果圆柱的底面半径为4cm，母线长为5cm，那么它的侧面积等于( )
（A）
（B）
（C）
（D）
14．关于
的一元二次方程
根的情况是( )
（A）有两个不相等实数根 （B）有两个相等实数根
（C）没有实数根 （D）根的情况无法判定
| 得分 | 评卷人 |
|
|
|
三、解答题（本大题共9个小题，满分70分）
| 得分 | 评卷人 |
15．（本小题5分）计算：20050－│－
│+
+
| 得分 | 评卷人 |
16．（本小题6分）解方程：
| 得分 | 评卷人 |
17．（本小题8分）
已知一个二次函数的图象经过点（0，0），（1，﹣3），（2，﹣8）．
（1）求这个二次函数的解析式；
（2）写出它的对称轴和顶点坐标．
| 得分 | 评卷人 |
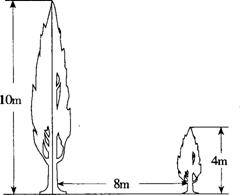
18．（本小题6分）
如图，有两棵树，一棵高10米，另一棵高4米，两树相距8米. 一只小鸟从一棵树的树梢飞到另一棵树的树梢，问小鸟至少飞行多少米？
| 得分 | 评卷人 |
19．（本小题9分）
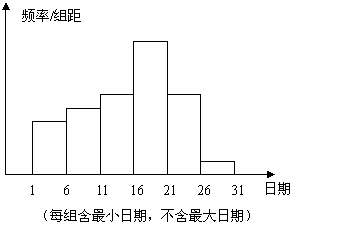在学校开展的综合初中活动中，某班进行了小制作评比，作品上交时间为5月1日至30日，评委会把同学们上交作品的件数按5天一组分组统计，绘制了频率分布直方图如图所示，已知从左至右各长方形的高的比为2∶3∶4∶6∶4∶1，第三组的频数为12，请解答下列问题：
(1)本次活动共有多少件作品参加了评比？
(2)哪组上交的作品数量最多？有多少件？
(3)经过评比，第四组和第六组分别有10
件和2件作品获奖，问这两组哪组获奖
率较高？
| 得分 | 评卷人 |
20．（本小题8分）
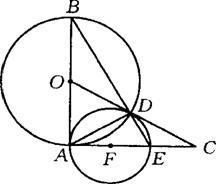
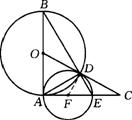
如图，AB是⊙O的直径，过A作⊙O的切线，在切线上截取AC=AB，连结OC交⊙O于D，连结BD并延长交AC于E，⊙F是△ADE的外接圆，F在AE上．
求证：(1)CD是⊙F的切线；(2)CD=AE．
 |
| 得分 | 评卷人 |
21．（本小题9分）
今年，我国政府为减轻农民负担，决定在5年内免去农业税．某乡今年人均上缴农业税25元，若两年后人均上缴农业税为16元，假设这两年降低的百分率相同．
（1）求降低的百分率；
（2）若小明家有4人，明年小明家减少多少农业税？
（3）小明所在的乡约有6000农民，问该乡农民明年减少多少农业税．
| 得分 | 评卷人 |
22．（本小题9分）
已知：△ABC中，AB＝10
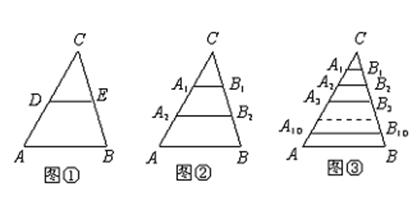
（1）如图①，若点D、E分别是AC、BC边的中点，求DE的长；
（2）如图②，若点A1、A2把AC边三等分，过A1、A2作AB边的平行线，分别交BC边于点B1、B2，求A1B1＋A2B2的值；
（3）如图③，若点A1、A2、…、A10把AC边十一等分，过各点作AB边的平行线，分别交BC边于点B1、B2、…、B10．根据你所发现的规律，直接写出A1B1＋A2B2＋…＋A10B10的结果．
| 得分 | 评卷人 |
23．（本小题10分）
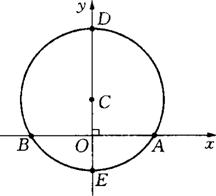
已知：如图，在平面直角坐标系中，点C在
轴上，以C为圆心，4cm为半径的圆与轴相交于点A、B，与轴相交于D、E，且︵AB=︵BD ．点P是⊙C上一动点（P点与A、B点不重合）．连结BP、AP．
（1）求∠BPA的度数；
（2）若过点P的⊙C的切线交轴于点G，是否存在点P，使△APB与以A、G、P为顶点的三角形相似？若存在，求出点P的坐标；若不存在，说明理由．
初三毕业考试数学试卷参考答案
一、填空题（每小题3分，共18分）
1．4 2．3.9×10-5 3．x≠-2 4．(3，2)
5．AB=DC或∠ACB=∠DBC或OB=OC或OA=OD 6．n(n+1)-n=n2
二、选择题（每小题4分，共32分）
7.B 8.B 9.A 10.B 11.C 12.C 13.D 14.A
三、解答题（本大题共9个小题，满分70分）
15．（本小题5分）20050－│－│++
=1－+2+－1=2
16．（本小题6分）
,
即：y2-2y-3=0 ， 解得y1=3，y2=-1 当y1=3时，x=-1，当y2=-1时，x=
经检验，x1= -1, x2=是原方程的根
∴x1= -1, x2=
17．（本小题8分）(1)设这个二次函数的解析式为：y=ax2+bx+c，
∵二次函数图象经过三点(0，0)，(1，-3)，(2，-8)， ∴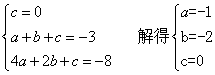
∴这个二次函数的解析式为：y=-x2-2x；
(2) ∵y=-x2-2x=-(x+1)2+1
∴这个二次函数的对称轴为x=-1，顶点坐标为(-1，1)．
18．（本小题6分）如图，设大树高为AB=10m，
小树高为CD=10m，
过C点作CE⊥AB于E， 则EBDC是正方形，
连接AC，∴EB=4m，EC=8m，AE=AB-EB=10-4=6m
在Rt△AEC中，
19．（本小题9分）(1) 60件；(2)第四组交了18件； (3)第六组获奖率较高；
20．（本小题8分）(1)连结DF，∵OA=OD，∴∠OAD=∠ODA，又∵FA=FD，∴∠FAD=∠FDA，∴∠BAC=∠FDO．又∵ AC为⊙O的切线，∴∠BAC=90°． ∴∠FDO=90°．
即：CD⊥DF． ∴CD是O F的切线；
(2) ∵DF⊥CD ∴Rt△CDF∽Rt△CAO
∴DF/CD=OA/AC 又∵AC=AB=2OA
∴DF/CD=OA/2OA=1/2 CD=2DF．
∵AE=2DF．∴CD=AE．
21．（本小题9分）（1）设降低的百分率为x，
依题意有
解得x1＝0.2＝20％，x2 ＝1.8(舍去)
（2）小明全家少上缴税 25×20％×4＝20（元）
（3）全乡少上缴税 6000×25×20％＝30000（元）
22．（本小题9分）（1）∵D、E分别是AC、BD的中点，且AB=10，∴DE=
AB=5.
（2）设A1B1=x,则A2B2=2x. ∵A1、A2是AC的三等分点，且A1B1∥A2B2∥AB，∴A2B2是梯形A1ABB1的中位线，即： x+10=4x，得x=
，∴A1B1＋A2B2=10
[另解] 分别过B1、B2作B1C1∥CA，作B2C2∥CA，交AB于C1、C2，则C1、C2是AB的三等分点，∴A1B1=AC1=，A2B2=
，∴A1B1＋A2B2=10
（3）同理可得：A1B1＋A2B2＋…＋A10B10=
23．（本小题10分）(1)∠BPA=60° 或∠BPA=120°；
(2)设存在点P，使△APB与以点A、G、P为顶点的三角形相似．
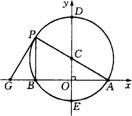
①当P在弧EAD上时，（图1） GP切O C于点P， ∴∠GPA=∠PBA
又∵∠GAP是△ABP的外角，∴∠GAP>∠BPA，∠GA P>∠PBA．
欲使△APB与以点A、G、P为顶点的三角形相似，须∠GAP=∠PAB=90°
∴BP为⊙C的直径．在Rt△PAB中，∠BPA=60°，PB=8，
∴PA=4，AB=4
OA=2 ∴P(2，4)．
②当P在弧EBD上时，（图2）在△PAB和△GAP中，
∵∠PBA是△GBP的外角，
∴∠PBA>∠PGB． 又∵∠PAB=∠GAP，
欲使△APB与以点A、G、P为顶点的三角形相似，须∠APB=∠PGB
∴GP切⊙C于点P，∴∠GPB=∠PAG
由三角形内角和定理知：∠ABP=∠GBP
∴∠ABP=∠GBP=90°
在Rt△PAB，∠BPA=60°，PA=8，
∴PB=4，AB=4∴OB=2 ∴P(-2，4)．
∴存在点P1(2，4)、P2(-2，4)使△APB与以点A、G、P为顶点的三角形相似．
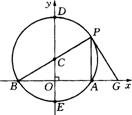
图1 图2