初中毕业生学业考试数学卷3

初中毕业生学业考试数学卷

数学试卷

说明：1．全卷七大题，共8页，考试时间90分钟，满分100分．

2．答题前，请将考场号、试室号、座位号、考生号、姓名写在试卷密封线内．不得在试卷上作任何标记．

3．解答选择题时，请将选项的字母代号写在答题表一内；解答填空题时，请将答案写在答题表二内；做解答题、证明题、应用题、分析题、探究题时，请将解答过程和结果写在指定的位置上．

题号	一	二	三						四	五	六	七
	1－10	11－15	16	17	18	19	20	21	22	23	24	25
得分

得分	一、选择题（本题有10小题，每题3分，共30分）   阅卷人

答题表一

题号	1	2	3	4	5	6	7	8	9	10
答案

每小题给出4个答案，其中只有一个是正确的．请把正确答案的字母代号填在上面的答题表一内．

1． 某物体的三视图是如图1所示的三个图形，那么该物体形状是

A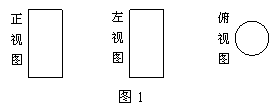．长方体　　　　

B． 圆锥体　　　 　

C．立方体

D．圆柱体

２．今年6月5日是第33个世界环境日，其主题是“海洋存亡，匹夫有责”．目前全球海洋总面积约为36105.9万平方公里，用科学记数法(保留三个有效数字)表示为

A．3.61×10⁸平方公里　　　　　　　　 　B．3.60×10⁸平方公里

C．361×10⁶平方公里　　　　　　　　　  D．36100万平方公里

3． 要使二次根式有意义，字母x必须满足的条件是

A．x≥1　　　　　 B．x＞－1　　　　  C．x≥－1　　　　D．x＞1

4．下列轴对称图形中（如图2），只有两条对称轴的图形是

　　　　　　 　　　　　　　　　　　　　　 

　　　　　　　　　　　　　　　   

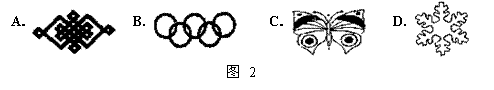
5．如图3，AB⊥BC，∠ABD的度数比∠DBC的度数的两倍少15°，设∠ABD和∠DBC的度数分别为x、y，那么下面可以求出这两个角的度数的方程组是

 

A．　  B．　

C．　 D．

6．为筹备班级的初中毕业联欢会，班长对全班学生爱吃哪几种水果作了民意调

查．那么最终买什么水果，下面的调查数据中最值得关注的是

A．中位数　　　　B．平均数　　　　 C．众数　　　　 D．加权平均数

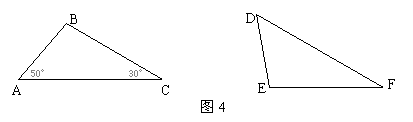
7．如图4，若△ABC≌△DEF，则∠E等于

A．30°　　　　  B． 50°　　　　C．60°　　　　　 D．100°

8．如图5，一棵大树在一次强台风中于离地面5米处折断倒下，倒下部分与地面

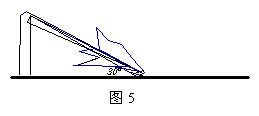成30°夹角，这棵大树在折断前的高度为

A．10米　　　  

B．15米　　　　

C．25米　　　　

D．30米

9．图6是深圳市南山区地图的一角，用刻度尺、量角器测量可知，深圳大学(　)

大约在南山区政府(★)的什么方向上

A．南偏东80°　　B．南偏东10°　 C．北偏西80°　D．北偏西10°

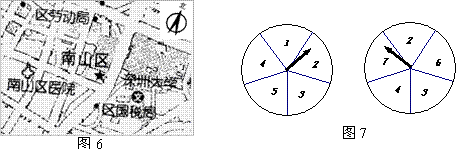
10．图7所示的两个圆盘中，指针落在每一个数上的机会均等，那么两个指针同

时落在偶数上的概率是

A．　　　　　　B．　　　　　 C．　　　　　  D．

	二、填空题（本题有5小题，每题3分，共15分．请 把答案填在答题表二内相应的题号下．）

得分	阅卷人

答题表二

题 号	11	12	13	14	15
答 案

答案请填在上面答题表二内

11．图8是2004年6月份的日历，如图中那样，用一个圈竖着圈住3个数．如果被圈的三个数的和为39，则这三个数中最大的一个为

　　　　　　　　　　　　  ．

日	一	二	三	四	五	六
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30

图8

答案请填在上面答题表二内

12．如图9，D、E分别是△ABC的边AC、AB上的点，请你添加一个条件，使

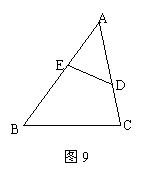
△ADE与△ABC相似．你添加的条件是

　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　．

13．老师给出一个函数，甲、乙、丙各正确指出了这个函数的一个性质：

甲：函数的图象经过第一象限；　　　　　 乙：函数的图象经过第三象限；

丙：在每个象限内，y随x的增大而减小．

答案请填在上面答题表二内

请你根据他们的叙述构造满足上述性质的一个函数：

　　　　　　　　　　　　  ．

14．如图10，在⊙O中，已知∠ACB=∠CDB=60°，AC=3，则△ABC的周长是

答案请填在上面答题表二内

　　　　　　　　　　　　　  ．

答案请填在上面答题表二内

15．小洪和小斌两人参加体育项目训练，近期的5次测试成绩如图11所示，根据分析，你认为他们中成绩较为稳定的是

　　　　　　　　　　　　　　　 ．

16．（4分）计算：

三、解答题（本部分共27分，第16、17、21题各4分，第18、19、20题各5分）

得分	阅卷人
	（结果保留根号）

解：原式＝

17．（4分）有这样一道题：“计算：的值，其中．”甲同学把“”错抄成“”，但他的计算结果也是正确的．你说这是怎么回事？

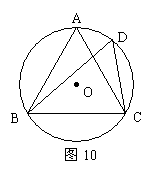得分	阅卷人

解：

得分	18．（5分）解方程：   阅卷人

解：

	19．（5分）如图12，一位篮球运动员跳起投篮，球沿抛物线运行，然后准确落入篮框内．已知篮框的中心离地面的距离为3.05米．

得分	阅卷人

（1） (2分)　球在空中运行的最大高度为多少米？

解：

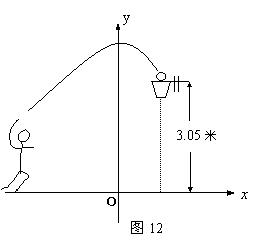（2） (3分)　如果该运动员跳投时，球出手离地面的高度为2.25米，请问他距离篮

框中心的水平距离是多少？

解：

	20．（5分）在“深圳读书月”活动中，小华在书城买了一套科普读物，有上、中、下三册，要整齐的摆放在书架上，有哪几种摆法？其中恰好摆成“上、中、下”顺序的概率是多少？

得分	阅卷人

解：

	21．（4分）平移方格纸中的图形（如图13），使A点平移到A′ 点处，画出平移后的图形，并写上一句贴切、诙谐的解说词．

得分	阅卷人

解：

	解说词：

得分	四、证明题（本题5分）   阅卷人

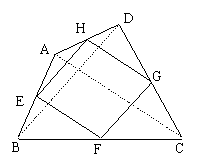
22．如图14，在四边形ABCD中，E、F、G、H分别是边AB、BC、CD、DA的中点，请添加一个条件，使四边形EFGH为菱形，并说明理由．

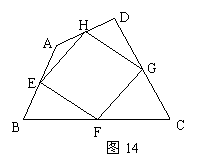解：添加的条件：　　　　　　　　  　　　 

　　理由：

　　　　　　　　　　　　　　　　　　　　　 

得分	五、应用题（本题5分）   阅卷人

23．某地电话拨号入网有两种收费方式，用户可以任选其一：

（A）　　  计时制：0.05元/分；　(B) 包月制：50元/月（限一部个人住宅电话上网）．

此外，每一种上网方式都得加收通信费0.02元/分．

（1） （4分）请你分别写出两种收费方式下用户每月应支付的费用y（元）与上网时间x（小时）之间的函数关系式；

解：

（2） （1分） 若某用户估计一个月内上网的时间为20小时，你认为采用哪种方式较为合算？

解：

得分	六、图表阅读分析题（本题8分）   阅卷人

24．记者从教育部获悉，今年全国普通高校招生报名人数总计723万．除少部分

参加各省中专、中职、中技考试的考生外，参加统考的考生中有文史类、理工类、文理综合类．下面的统计图（图15）反映了今年全国普通高校招生报名人数的部分情况，请认真阅读图表，解答下列问题：

(1)　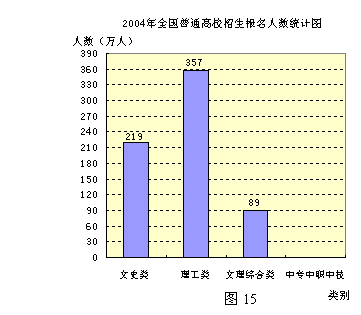　 (3分) 请将该统计图补充完整；

(2)　　(3分) 请你写出从图中获得的

三个以上的信息；

解：

(3)　　 (2分) 记者随机采访一名考生，

采访到哪一类考生的可能性较大？

解：

得分	七、综合探究题（本题10分）   阅卷人

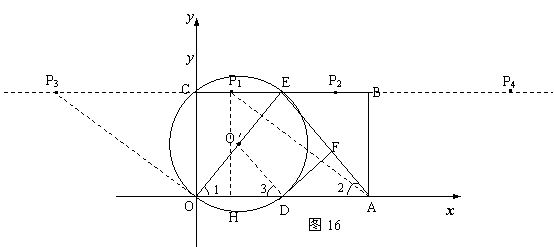
25．如图16，在平面直角坐标系中，矩形ABCO的面积为15，边OA比OC大2．

E为BC的中点，以OE为直径的⊙O′交轴于D点，过点D作DF⊥AE于点F．

（1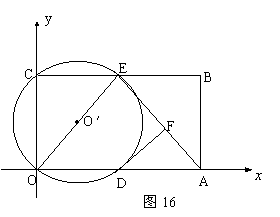）　　　 (2分)　求OA、OC的长；

解：

（2）　(3分)　求证：DF为⊙O′的切线；

证明：

（3）　　　 (5分)　小明在解答本题时，发现△AOE是等腰三角形．由此，他断定：“直线

BC上一定存在除点E以外的点P，使△AOP也是等腰三角形，且点P一定在⊙O′外”．你同意他的看法吗？请充分说明理由．

解：

	祝贺你做完了考题,请再仔细检查一遍,看看有没有错的、漏的,别留下什么遗憾哦!

数学参考答案及评分建议

一、选择题（本题有10小题，每题3分，共30分）

题号	1	2	3	4	5	6	7	8	9	10
答案	D	A	C	A	B	C	D	B	A	B

二、填空题（本题有5小题，每题3分，共15分）

题号	11	12	13	14	15
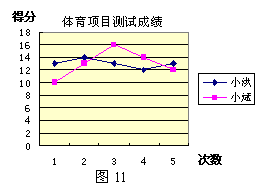
答案	20	∠AED=∠C、或∠ADE=∠B 或（只写一个）	（比例系数为正数即可）	9	小洪

说明：填空题12题的答案写成或DE//BC也可以；13题的答案画出图形或

列出表格符合反比例函数性质，也给分。

三、解答题

16、原式=　　　　　　　　　　　 ……　(3分) (每个一分)

　　　　=　　　　　　　  　　　　　　　……　(4分)

　

17、∵ =

=

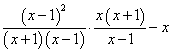
=0　　　　　　　　　　　  ……（3分）

只要的取值使这个代数式有意义，其值就为0．

∴错抄成不影响结果，都为0 ．　　 ……（4分）　

18、 方程两边同乘以，得　　　　　　　　　　　　　 …… (1分)

　　　　　　　　　　　　　　  ……（2分）

　　　　

∴　　 　　　　　　　　　　　 　　　　　 ……（3分）

检验：把代入=54≠0　　　　　　　　　  …… （4分）

∴原方程的解为．　　　　　　　　　　　　　　　 …… （5分）

19、⑴ ∵抛物线 的顶点坐标为（0，3.5）

∴球在空中运行的最大高度为3.5米 ．　　　　　　　　  ……（2分）

⑵ 在中

当时　　

∴　　  ∴

又∵＞0　　　　∴　　　　　　　　　　　　　　　…… （3分）

当时　　

∴　　  ∴

又∵＜0　　　　∴　　　　　　　　　　　　　　 …… （4分）

故运动员距离篮框中心水平距离为米．　　　　…… （5分）

20、摆法共有如下6种：上、中、下； 上、下、中；

中、上、下； 中、下、上；

下、上、中； 下、中、上．　　　　  　　…… （3分）

　　 恰好摆成“上、中、下”的概率为．　　　　　　　　　　  …… （5分）

21、平移图形给3分，解说词给1分．

四．证明题

22、条件：对角线相等　　　　 …… （2分）

理由：连结AC、BD　　　　　　 

∵在△ABC中，AE=BE　 BF=CF

　　　　∴EF为△ABC的中位线

　　　　∴EF=AC　　　　　　  …… （3分）

　　同理可得FG=BD　GH=AC　HE=BD

　　 又∵AC= BD　 （添加条件）

　　 ∴EF=FG= GH= HE

　　 故四边形EFGH为菱形.　　　　　　　　　　　　　　　　  …… （5分）

说明：本题条件的给定只要具有对角线相等即可．

五．应用题

23、⑴ 依题意，得

计时制：

　　　 即　　　　　　　　　　　　　　　　　  …… （2分）

包月制：

　　　 即　　　　　　　　　　　　　　　  …… （4分）

⑵ 当时

计时制：（元）

 包月制：（元）

　若某用户估计一个月上网20小时，采用包月制较为合算． …… （ 5分）

六．图表阅读分析题

24、⑴ 说明：本小题考生正确写出三个信息，即可给3分．

⑵ 略（画图正确）　　　　　　　　　　　　　　　　　　　  …… （6分）

⑶ 理工类考生可能性最大．　　　　　　　　　　　　　　　  …… （8分）

七．综合探究题

25、解：

（1）在矩形OABC中，设OC=x　则OA= x+2，依题意得

　　　　  解得：

（不合题意，舍去）　　∴OC=3，　OA=5　　　　　　 ……　(2分)

（只要学生写出OC＝3，OA＝5即给2分）

（2）连结O′D

  在矩形OABC中，OC=AB，∠OCB=∠ABC=90，CE=BE=　　　　　　　　　 

∴ △OCE≌△ABE　

∴EA=EO　　∴∠1=∠2

在⊙O′中，　∵ O′O= O′D　　　∴∠1=∠3

 ∴∠3=∠2　　  ∴O′D∥AE，　　

 ∵DF⊥AE　　 ∴ DF⊥O′D

又∵点D在⊙O′上，O′D为⊙O′的半径 ，∴DF为⊙O′切线。 …　(5分)

(3)　　　 不同意.

理由如下:

①当AO=AP时，

以点A为圆心，以AO为半径画弧交BC于P₁和P₄两点

过P₁点作P₁H⊥OA于点H，P₁H = OC = 3，∵A P₁= OA = 5

∴A H = 4， ∴OH =1　　　　

求得点P₁（1，3）　　同理可得：P₄（9，3）　　　　　　　  …… (7分)

②当OA=OP时，

同上可求得:：P₂（4，3），P₃（4，3）　　　　　　　　　　 …… (9分)

因此，在直线BC上，除了E点外，既存在⊙O′内的点P₁，又存在⊙O′外的点P₂、P₃、P₄，它们分别使△AOP为等腰三角形。　　　　　　　　　　  …… (10分)

其它解法，请参照评分建议酌情给分。