初中毕业生学业考试数学卷
数学试卷
说明：1．全卷分第一卷和第二卷,共8页．第一卷为选择题，第二卷为非选择题．考试时
间90分钟,满分100分．
2．答题前,请将姓名、考生号、科目代号、试室号和座位号填涂在答题卡上；将考场、试室号、座位号、考生号和姓名写在第二卷密封线内．不得在答题卡和试卷上做任何标记.
3．第一卷选择题(1－10)，每小题选出答案后，用2B铅笔把答题卡上对应题目的
答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，凡答案写在第一卷上不给分；第二卷非选择题(11－22)答案必须写在第二卷题目指定位置上．
4．考试结束，请将本试卷和答题卡一并交回．
第一卷（选择题，共30分）
一、选择题（本大题共10小题，每小题3分，共30分）
每小题给出４个答案，其中只有一个是正确的．请用２B 铅笔在答题卡上将该题相对应的答案标号涂黑．
１．－３的绝对值等于
Ａ．
Ｂ．３ Ｃ．
Ｄ．
２．如图１所示，圆柱的俯视图是
 | |||||
 | |||||
 | |||||
图１ Ａ Ｂ Ｃ Ｄ
３．今年1—5月份，深圳市累计完成地方一般预算收入216.58亿元，数据216.58亿精确到
Ａ．百亿位 Ｂ．亿位 Ｃ．百万位 Ｄ．百分位
４．下列图形中，是轴对称图形的为
 | |||
 | |||
Ａ Ｂ Ｃ Ｄ
５．下列不等式组的解集，在数轴上表示为如图２所示的是
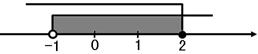Ａ．
Ｂ．
Ｃ．
Ｄ．
图2
６．班主任为了解学生星期六、日在家的学习情况，家访了班内的六位学生，了解到他们
在家的学习时间如下表所示．那么这六位学生学习时间的众数与中位数分别是
Ａ．4小时和4.5小时
| 学生姓名 | 小丽 | 小明 | 小颖 | 小华 | 小乐 | 小恩 |
| 学习时间 (小时) | 4 | 6 | ３ | ４ | 5 | 8 |
Ｂ．4.5小时和4小时
Ｃ．4小时和3.5小时
Ｄ．3.5小时和4小时
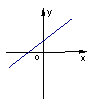
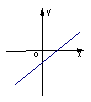
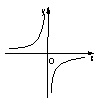
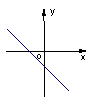
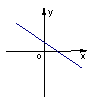７．函数
的图象如图3所示，那么函数
的图象大致是
图3 A B C D
８．初三的几位同学拍了一张合影作留念，已知冲一张底片需要0.80元，洗一张相片需要0.35元．在每位同学得到一张相片、共用一张底片的前提下，平均每人分摊的钱不足0.5元，那么参加合影的同学人数
Ａ．至多６人 Ｂ．至少６人 Ｃ．至多５人 Ｄ．至少５人
 |
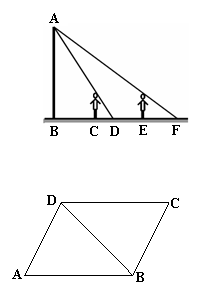９．如图4，王华晚上由路灯A下的B处走到Ｃ处时，测得
影子CD的长为１米，继续往前走３米到达Ｅ处时，测
得影子EF的长为2米，已知王华的身高是1.5米，那么
路灯A的高度AB等于
Ａ．4.5米 Ｂ．6米
Ｃ．7.2米 Ｄ．8米
图4
10．如图5，在□ABCD中，AB: AD = 3:2，∠ADB=60°，
那么cosＡ的值等于
Ａ．
Ｂ．
Ｃ．
Ｄ．
图5
深圳市2006年初中毕业生学业考试
数学试卷
| 题 号 | 二 | 三 | ||||||
| 11～15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | |
| 得 分 |
|
|
|
|
|
|
|
|
第二卷（非选择题，共70分）
| 得分 | 阅卷人 |
|
|
|
二、填空题(本大题共5小题，每小题3分，共15分)
请将答案填在答题表一内相应的题号下，否则不给分．
| 答题表一 | |||||
| 题 号 | 11 | 12 | 13 | 14 | 15 |
| 答 案 | |||||
11．某商场在“五一”期间推出购物摸奖活动，摸奖箱内有除颜色以外完全相同的红色、白色乒乓球各两个．顾客摸奖时，一次摸出两个球，如果两个球的颜色相同就得奖，颜色不同则不得奖．那么顾客摸奖一次，得奖的概率是
．
12．化简：
．
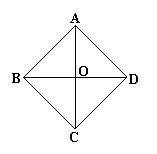
13．如图6所示，在四边形ABCD中，
，
对角线AC与BD相交于点O．若不增加任何字母与辅
助线，要使得四边形ABCD是正方形，则还需增加的
一个条件是
．
图6
14．人民公园的侧门口有9级台阶，小聪一步只能上１级台阶或２级台阶，小聪发现当台阶数分别为１级、２级、３级、４级、５级、６级、７级……逐渐增加时，上台阶的不同方法的种数依次为１、２、３、５、８、13、21……这就是著名的斐波那契数列．那么小聪上这９级台阶共有
种不同方法．
15．在△ABC中，AB边上的中线CD=3，AB=6，BC+AC=8，则△ABC的面积为
．
三、解答题（本大题有7题，其中第16、17题各6分；第18题７分；第19、20题各８分；第21、22题各10分，共55分）
| 得分 | 阅卷人 |
|
|
|
16．（6分）计算：
解：原式＝
| 得分 | 阅卷人 |
|
|
|
17．（6分）解方程：
解：
| 得分 | 阅卷人 |
|
|
|
18．（７分）如图7，在梯形ABCD中，AD∥BC, 
，
．（1）（３分）求证：
证明：
（2）（４分）若
，求梯形ABCD的面积．
解：
| 得分 | 阅卷人 |
|
|
|
19．（8分）某中学图书馆将图书分为自然科学、文学艺术、社会百科、数学四类.在“深圳读书月”活动期间，为了解图书的借阅情况，图书管理员对本月各类图书的借阅量进行了统计，图8-1和图8-2是图书管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图．请你根据图表中提供的信息,解答以下问题:
 |
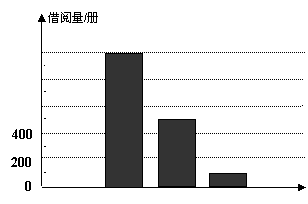| 频率分布表 | ||
| 图书种类 | 频数 | 频率 |
| 自然科学 | 400 | 0.20 |
| 文学艺术 | 1000 | 0.50 |
| 社会百科 | 500 | 0.25 |
| 数学 | ||
|
|
|
 | |||
|
（1）(2分)填充图8-1频率分布表中的空格．
（2）(2分)在图8-2中，将表示“自然科学”的部分补充完整．
（3）(2分)若该学校打算采购一万册图书,请你估算“数学”类图书应采购多少册较合适？
解：
（4）(2分) 根据图表提供的信息，请你提出一条合理化的建议．
| 得分 | 阅卷人 |
|
|
|
20．(8分)工艺商场按标价销售某种工艺品时，每件可获利45元；按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.
（1）(4分)该工艺品每件的进价、标价分别是多少元？
（2）(4分)若每件工艺品按（1）中求得的进价进货，标价售出，工艺商场每天可售出该工艺品100件．若每件工艺品降价1元，则每天可多售出该工艺品4件．问每件工艺品降价多少元出售，每天获得的利润最大？获得的最大利润是多少元?
| 得分 | 阅卷人 |
|
|
|
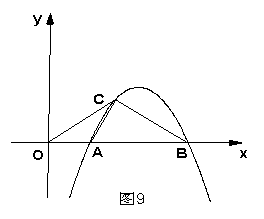21．(10分)如图9，抛物线
与
轴交于
、
两点（点在点的左侧），抛物线上另有一点
在第一象限，满足 ∠
为直角,且恰使△
∽△
.
(1)(3分)求线段
的长.
解：
(2)(3分)求该抛物线的函数关系式．
解：
(3)(4分)在轴上是否存在点
，使△
为等腰三角形？若存在，求出所有符合条件的点的坐标；若不存在，请说明理由.
解：
| 得分 | 阅卷人 |
|
|
|
22．(10分)如图10-1，在平面直角坐标系
中，点
在轴的正半轴上， ⊙交轴于 
两点，交
轴于
两点，且为
的中点，
交轴于
点，若点的坐标为（－2，0），
(1)(3分)求点的坐标.
解：
(2)(3分)连结
，求证：
∥
证明：
(3)(４分) 如图10-2，过点
作⊙的切线，交轴于点.动点
在⊙的圆周上运动时，
的比值是否发生变化，若不变，求出比值；若变化，说明变化规律.
解：
参考答案
一、选择题（本大题共10小题，每小题3分，共30分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | C | C | D | D | A | C | B | B | A |
二、填空题(本大题共5小题，每小题3分，共15分)
| 题 号 | 11 | 12 | 13 | 14 | 15 |
| 答 案 | 1/3 | 1/（m-3） | Ac=BD | 55 | 7 |
三、解答题（本大题有7题，其中第16、17题各6分；第18题７分；第19、20题各８分；第21、22题各10分，共55分）
16、-3/2
17、2
18、（1）略；（2）
19、（1）100，0.05；（2）略；（3）500；（4）略
20、（1）155，200；（2）10，4900。
21、（1）
；（2）
；（3）4个点：
22、（1）（0，4）；（2）提示，求OG的长，并得到OG：OC=OM：OB；（3）3/5