初中毕业生学业考试数学卷
说明：1．全卷分二部分，第一部分为选择题，第二部分为非选择题，共4页．考试时间90分钟，满分100分．
2．本卷试题，考生必须在答题卡上按规定作答；凡在试卷、草稿纸上作答的，其答案一律无效．答题卡必须保持清洁，不能折叠．
3．答题前，请将姓名、考生号、考场、试室号和座位号用规定的笔写在答题卡指定的位置上，将条形码粘贴好．
4．本卷选择题1－10，每小题选出答案后，用2B铅笔将答题卡选择题答题区内对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案；非选择题11－23，答案（含作辅助线）必须用规定的笔，按作答题目序号，写在答题卡非选择题答题区内．
5．考试结束，请将本试卷和答题卡一并交回．
第一部分 选择题
（本部分共10小题，每小题3分，共30分．每小题给出4个选项，其中只有一个是正确的）
1．
的相反数是（ ）
Ａ．
Ｂ． Ｃ．
Ｄ．
2．今年参加我市初中毕业生学业考试的考生总数为
人，这个数据用科学记数法表示为（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
3．仔细观察图1所示的两个物体，则它的俯视图是（ ）
 |
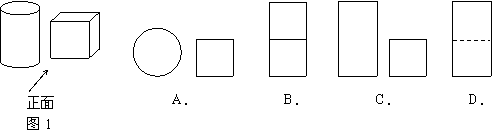4．下列图形中，不是轴对称图形的是（ ）
5．已知三角形的三边长分别是
；若
的值为偶数，则的值有（ ）
Ａ．
个 Ｂ．
个 Ｃ．
个 Ｄ．
个
6．一件标价为
元的商品，若该商品按八折销售，则该商品的实际售价是（ ）
Ａ．
元 Ｂ．
元 Ｃ．
元 Ｄ．元
7．一组数据，
，
，
，的方差是（ ）
Ａ． Ｂ． Ｃ． Ｄ．
8．若
，则
的值是（ ）
Ａ． Ｂ． Ｃ． Ｄ．
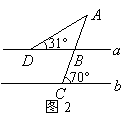
9．如图2，直线
，则
的度数是（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
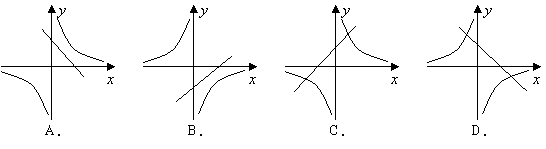10．在同一直角坐标系中，函数
与
的图象大致是（ ）
第二部分 非选择题
填空题（本题共5小题，每小题3分，共15分）
11．一个口袋中有4个白球，5个红球，6个黄球，每个球除颜色外都相同，搅匀后随机从袋中摸出一个球，这个球是白球的概率是 ．
12．分解因式：
．
13．若单项式
与
是同类项，则
的值是 ．
14．直角三角形斜边长是，以斜边的中点为圆心，斜边上的中线为半径的圆的面积是 ．
15．邓老师设计了一个计算程序，输入和输出的数据如下表：
| 输入数据 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| 输出数据 |
|
|
|
|
|
| … |
那么，当输入数据是
时，输出的数据是 ．
解答题（本题共8小题，其中第16题5分，第17题6分，第18题6分，第19题6分，第20题7分，第21题8分，第22题9分，第23题8分，共55分）
16．计算：
17．解不等式组，并把它的解集表示在数轴上：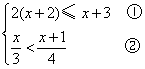
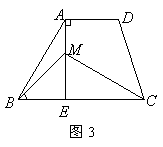18．如图3，在梯形
中，
，
，
是
上一点，
，
．
（1）求证：
．
（2）若
，求
的长．
19．2007年某市国际车展期间，某公司对参观本次车展盛会的消费者进行了随机问卷调查，共发放1000份调查问卷，并全部收回．①根据调查问卷的结果，将消费者年收入的情况整理后，制成表格如下：
| 年收入（万元） | 4.8 | 6 | 7.2 | 9 | 10 |
| 被调查的消费者人数（人） | 200 | 500 | 200 | 70 | 30 |
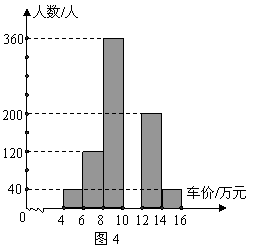
②将消费者打算购买小车的情况整理后，作出频数分布直方图的一部分（如图4）．
注：每组包含最小值不包含最大值，且车价取整数．请你根据以上信息，回答下列问题．
（1）根据①中信息可得，被调查消费者的年收入的众数是______万元．
（2）请在图4中补全这个频数分布直方图．
（3）打算购买价格
万元以下小车的消费者人数占被调查消费者人数的百分比是______．
 |
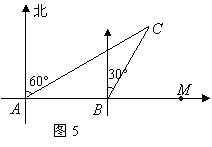
20．如图5，某货船以
海里／时的速度将一批重要物资从
处运往正东方向的处，在点处测得某岛
在北偏东
的方向上．该货船航行
分钟后到达
处，此时再测得该岛在北偏东
的方向上，已知在岛周围
海里的区域内有暗礁．若继续向正东方向航行，该货船有无触礁危险？试说明理由．
21．
两地相距
公里，甲工程队要在两地间铺设一条输送天然气管道，乙工程队要在两地间铺设一条输油管道．已知甲工程队每周比乙工程队少铺设公里，甲工程队提前周开工，结果两队同时完成任务，求甲、乙两工程队每周各铺设多少公里管道？
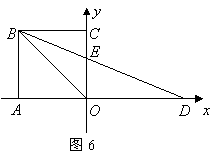
22．如图6，在平面直角坐标系中，正方形
的边长为，点
在轴的正半轴上，且
，
交
于点
．
（1）求
的度数．
（2）求点的坐标．
（3）求过
三点的抛物线的解析式．（计算结果要求分母有理化．参考资料：把分母中的根号化去，叫分母有理化．例如：①
；
②
；③
等运算都是分母有理化）
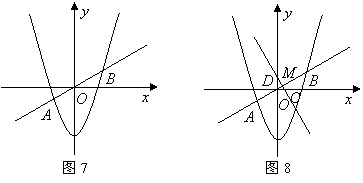
23．如图7，在平面直角坐标系中，抛物线
与直线
相交于两点．
（1）求线段
的长．
（2）若一个扇形的周长等于（1）中线段的长，当扇形的半径取何值时，扇形的面积最大，最大面积是多少？
（3）如图8，线段的垂直平分线分别交轴、
轴于
两点，垂足为点，分别求出
的长，并验证等式
是否成立．
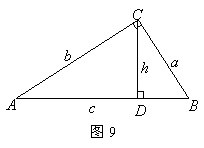（4）如图9，在
中，
，
，垂足为，设
，
，
．
，试说明：
．
参考答案
第一部分 选择题（本题共10小题，每小题3分，共30分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | B | A | A | D | B | B | C | C | C |
第二部分 非选择题
填空题（本题共5小题，每小题3分，共15分）
| 题号 | 11 | 12 | 13 | 14 | 15 |
| 答案 |
|
|
|
|
|
解答题（本题共7小题，其中第16题5分，第17题6分，第18题6分，第19题6分，第20题7分，第21题8分，第22题9分，第23题8分，共55分）
16． 
17．原不等式组的解集为 ≤
18．(1)证明略
(2)∴MC＝7
19．(1) 6 (2)略 (3) 
20． ∵
所以货船继续向正东方向行驶无触礁危险．
21．设甲工程队每周铺设管道公里,则乙工程队每周铺设管道(
)公里
根据题意, 得 
解得
，
经检验，都是原方程的根
但不符合题意,舍去
∴
答: 甲工程队每周铺设管道2公里,则乙工程队每周铺设管道3公里．
22．(1）∴
∴
（2）点E的坐标是
，
）
（3）设过B、O、D三点的抛物线的解析式为
∵B（-1，1），O（0，0），D（
，0）
∴
解得，
所以所求的抛物线的解析式为
23．（1） ∴A（-4，-2），B（6，3）
分别过A、B两点作
轴，
轴，垂足分别为E、F
∴AB=OA+OB
（2）设扇形的半径为，则弧长为
，扇形的面积为
则
∵
∴当
时，函数有最大值
（3）过点A作AE⊥轴，垂足为点E
∵CD垂直平分AB，点M为垂足
∴
∵
∴△AEO∽△CMO
∴
∴
∴
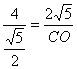同理可得
∴
∴
∴
（4）等式
成立．理由如下：
∵
∴
∴
∴
∴
∴
∴
∴
∴