初中毕业生学业考试数学卷
与高中阶段学校招生考试
数学试卷
| 考生须知 | 1．全卷分第一卷（选择题，满分40分，共2页）和第二卷（非选择题，满分110）分共8页），全卷满分150分；考试时间 l20分钟． 2．请认真填写答题卡和第一卷密封线内的有关内容，并在试卷右下角的座位号处填上 自己的座位号． 3．考试结束，将第一卷、第二卷和答题卡一并交回. 4．在考试中可以使用规定型号的科学计算器． |
“没有比人更高的山，没有比脚更长的路”．亲爱的同学们，准备好了吗？请相信自己，沉着应答，你一定能愉快地完成这次测试之旅，祝你成功！
第一卷（选择题，满分 40分，共2页）
一、精心选一选（本大题共l0小题，每小题4分，共40分．
每小题给出四个答案，其中只有一个是正确的）.
1．已知a-
=0，则a的值是
A.± B.-
C.
D.1.4
2．下列交通标志中，既是轴对称图形又是中心对称图形的是
 |
3．下列的运算中，其结果正确的是
A.
B.16x2-7x2 = 9 C.x8÷x2 = x4 D.x (-xy)2=x2y2
4．下列图形中可能是正方体展开图的是
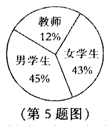5．某校师生总人数为l000人，其中男学生、女学生和教师所占的比例如图所示，则该校男学生人数为
A. 430人
B. 450人
C. 550人
D. 570人
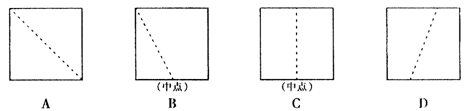
6．下列各图中，沿着虚线将正方形剪成两部分，那么由这两部分既能拼成平行四边形，又能拼成下角形和梯形的是
7．今年，我市某果农的荔枝又获丰收，预计比去年增产15 %，去年他卖荔枝收人3万元，若今年的价格和去年的持平，都是6元/公斤，则他今年的荔枝约可卖
A.4.5×104元 B. 4×104元 C.3.45×104元 D.5×104元
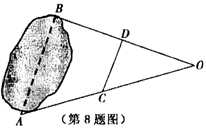8．如图，小明想用皮尺测最池塘A、B间的距离，但现有皮尺无法直接测量，学习数学有关知识后，他想出了一个主意：先在地上取一个可以直接到达A、B两点的点O，连接OA、OB，分别在OA、OB上取中点C、D，连接CD，并测得CD = a，
由此他即知道A、B距离是
A.
B.2a
C.a D.3a
9．已知点P是反比例函数
的图像上任一点，过P点分别作x轴，y轴的平行线，若两平行线与坐标轴围成矩形的面积为2，则k的值为
A.2 B.-2 C.±2 D.4
10．为了估计湖里有多少条鱼，先从湖里捕捞100条鱼都做上标记，然后放回湖中去，经过一段时间，待有标记的鱼完全混合于鱼群后，第二次再捕捞100条鱼，发现其中10条有标记，那么你估计湖里大约有鱼
A. 500条 B. 600条
C. 800 条 D. 1000条
茂名市2006年初中毕业生学业考试
与高中阶段学校招生考试
数 学 试 卷
| 题号 | 二 (11～15) | 三 (16～18) | 四 (19～20) | 五 | 六 | 总分 | |||
| 21 | 22 | 23 | 24 | 25 | |||||
| 得分 | |||||||||
第二卷（非选择题，满分 110 分，共 8 页）
二、耐心填一填（本大题共5小题，每小题4分，共20分．请你把答案填在横线的上方）．
11．在①长方体、②球、③圆锥、④圆柱、⑤三棱柱这五种几何体中，其主视图、左视图、俯视图都完全相同的是
（填上序号即可）.
12．分解因式：ax2+6ax+9a= .
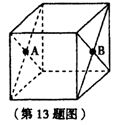
13．如图，点A、B分别是棱长为2的正方体左、右两侧面的中心，一蚂蚁
从点A沿其表面爬到点B的最短路程是 .
14. 若
，则
.
15. 甲、乙、丙、丁四人参加某校招聘教师考试，试后甲、乙两人去询问成绩。请你根据下面回答者对甲、乙两人回答的内容进行分析，则这四人的名次排列共可能有 种不同情况。
三、细心做一做（本大题共3小题，每小题8分，共24分）
16．已知：两个分式
.
.其中
x≠±1.下面三个结论：①A=B，②A、B为倒数，
③A、B互为相反数。请问这三个结论中哪一个结论
正确？为什么？
解：
17. 如图，在平面直角坐标系xoy中，直角梯形OABC, BC//AO, A（-2, 0), B（-l, 1)，将直角梯．形OABC绕点O顺时针旋转900后，点A、B、C分别落在点A′、B′、C′处.请你解答下列问题：
(l）在如图直角坐标系xoy中画出旋转后的梯形O′A′B′C′; (4分）
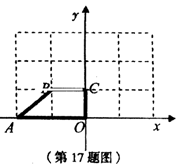(2）求点A旋转到A′所经过的弧形路线长 （4分）
18．甲、乙两人用如图所示的两个分格均匀的转盘做游戏：分别转动两个转盘，若转盘停止后，指针指向一个数字（若指针恰好停在分格线上，则重转一次），用所指的两个数字作乘积，如果积大于10，那么甲获胜；如果积不大于10，那么乙获胜。清你解决下列问题：
(l）利用树状图（或列表）的方法表示游戏所有可能出现的结果； (4分）
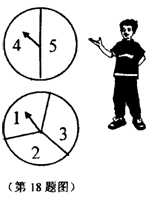(2）求甲、乙两人获胜的概率。（4分）
解：
四、沉着冷静，周密考虑（本大题2小题，每小题8分，共16分）
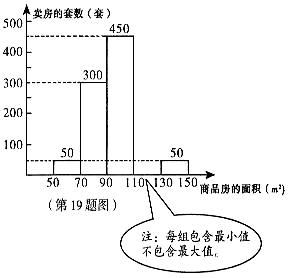19．现从我市区近期卖出的不同面积的商品房中
随机抽取1000套进行统计，并根据结果绘出
如图所示的统计图，请结合图中的信息，
解答下列问题：
(l）卖出面积为110-130cm2，的商品房有
套，并在右图中补全统计图；(4分）
(2）从图中可知，卖出最多的商品房约占全部
卖出的商品房的 %; (2分）
(3）假如你是房地产开发商，根据以上提供的信息，你会多建住房面积在什么范围内的住房？为什么？ (2 ）
解：
20. 先阅读，再填空解题：
(1)方程：x2-x-2=0 的根是：x1=-3, x2=4，则x1+x2=1，x1·x2=12；
(2)方程2x2-7x+3=0的根是：x1=
, x2=3，则x1+x2=
，x1·x2=
；
(3)方程x2-3x+1=0的根是：x1= , x2= .
则x1+x2= ，x1·x2= ；
根据以上（1)(2)(3）你能否猜出：
如果关于x的一元二次方程mx2+nx+p=0（m≠0且m、n、p为常数）的两根为x1、x2，那么x1+x2、x1、x2与系数m、n、p有什么关系？请写出来你的猜想并说明理由.
解：
五、开动脑筋，再接再厉（本大题共3小题．每小题10分，共30分）
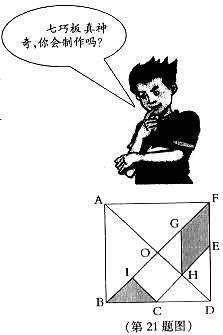21.（本小题满分10分）
七巧板是我们祖先的一项创造，被誉为“东方魔板”，
如图是一副七巧板，若已知S△BPC=1,请你根据七巧板
制作过程的认识，解决下列问题：
(1)求一只妈蚁从点A沿A→B→C→H→E所走的路线
的总长（结果精确到0.01);(5分）
(2)求平行四边形EFGH的面积.（5分）
解：
22.（本小题满分10分）
为了鼓励居民节约用水，我市某地水费按下表规
定收取：
(l）若某户用水量为x吨，需付水费为y元，则水费y
（元）与用水量x(吨）之间的函数关系式是：
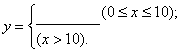(4分)
(2）若小华家四月份付水费17元，问他家四月份用水多少吨？ (3分）
(3）已知某住宅小区100户居民五月份交水费共1682元，且该月每户用水量均不超过15吨（含15吨），求该月用水量不超过10吨的居民最多可能有多少户？ (3分）
23. (本小题满分10分）
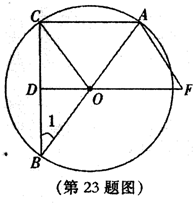如图，已知△ABC内接于⊙O,AB是直径，D是BC的中点，
连接DO并延长到F使AF=OC.
(1)写出途中所有全等的三角形（不用证明）；（4分）
(2)探究：当∠1等于多少都市，四边形OCAF是菱形？请回答并
给予证明.（6分）
解：
六、充满信心，成功在望（本大题共2小题，每小题10分，共20分）
24.（本小题满分10分）
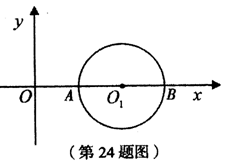
已知：半径为1的⊙O1与X轴交于A、B 两点，圆心O1
的坐标为（2, 0)，二次函数y=-x2+bx+c的图象经过A、B
两点，其顶点为F.
（1）求 b、c的值及二次函数顶点F的坐标； (4分）
（2）写出将二次函数y=-x2+bx+c的图象向下平移1个
单位再向左平移2个单位的图象的函数表达式；
（2分）
（3）经过原点O的直线
与⊙O相切，求直线的函数表达式.(4分）
解：
25.（本小题满分10分）
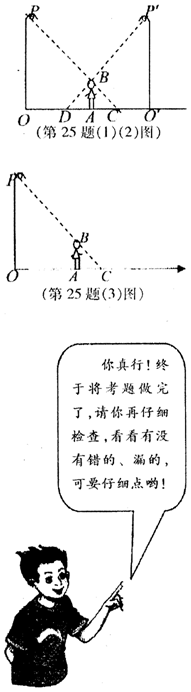
如图，李华晚上在路灯下散步．已知李华的
身高AB=h,灯柱的高OP=O/P/=,两灯柱之间的距离
OO/=m.
(l）若李华距灯柱OP的水平距离OA=a，求他影
子AC的长；(3分）
(2）若李华在两路灯之间行走，则他前后的两个影子的长度之和（DA+AC)是否是定值？请说
明理由；（3分）
(3）若李华在点A朝着影子（如图箭头）的方向以
匀速行走，
试求他影子的顶端在地面上移动的速度
. (4分）
解：
初中毕业生学业考试数学卷
数学试卷参考答案及评分标准
