初中毕业生学业考试数学试卷
说明:1.全卷共8页,考试时间90分钟,满分120分.
2.下列公式供解题时参考:
(1)扇形弧长公式:![]() .
.
(2)一组数据的方差公式:![]() .
.
一、选择题:每小题3分,共15分.每小题给出四个答案,其中只有一个是正确的,把所选答案的编号填写在题目后面的括号内.
1.观察下面图案,在A,B,C,D四幅图案中,能通过图案(1)平移得到的是( )
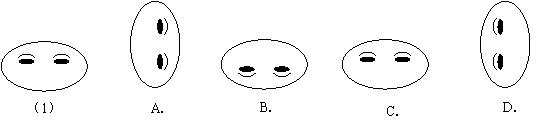 |
2.下列事件中,必然事件是( )
 A.中秋节晚上能看到月亮 B.今天考试小明能得满分
A.中秋节晚上能看到月亮 B.今天考试小明能得满分
C.早晨的太阳从东方升起 D.明天气温会升高
3.如图1,晚上小亮在路灯下散步,在小亮由![]() 处走
处走
到![]() 处这一过程中,他在地上的影子( )
处这一过程中,他在地上的影子( )
A.逐渐变短 B.逐渐变长
C.先变短后变长 D.先变长后变短
4.比较![]() 的大小,正确的是( )
的大小,正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.圆心距为6的两圆相外切,则以这两个圆的半径为根的一元二次方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
 二、填空题:每小题3分,共30分.答案填在横线上.
二、填空题:每小题3分,共30分.答案填在横线上.
6.计算![]() .
.
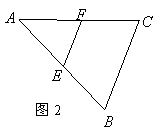
7.如图2,在![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,
若![]() ,则
,则![]() cm.
cm.
8.函数![]() 的自变量
的自变量![]() 的取值范围是
.
的取值范围是
.
9.近视眼镜的度数![]() (度)与镜片焦距
(度)与镜片焦距![]() (米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数
(米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数![]() 与镜片焦距
与镜片焦距![]() 之间的函数关系式为 .
之间的函数关系式为 .
 10.不等式组
10.不等式组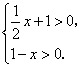 的解为
.
的解为
.
11.在中国地理地图册上,连结上海、香港、台湾三地构
成一个三角形,用刻度尺测得它们之间的距离如图3所示.
飞机从台湾直飞上海的距离约为1286千米,那么飞机从台
湾绕道香港再到上海的飞行距离约为 千米.
12.小明与父母从广州乘火车回梅州参观叶帅纪念馆,他们买到的火车票是同一排相邻的三个座位,那么小明恰好坐在父母中间的概率是 .
 13.将4个数
13.将4个数![]() 排成2行、2列,两边各加一条竖直线记成
排成2行、2列,两边各加一条竖直线记成![]() ,定义
,定义![]()
![]() ,上述记号就叫做2阶行列式.若
,上述记号就叫做2阶行列式.若![]()
![]() ,则
,则![]() .
.
14.如图4,已知![]() 为等腰三角形纸片
为等腰三角形纸片![]() 的底边,
的底边,
![]() .将此三角形纸片沿
.将此三角形纸片沿![]() 剪
剪
开,得到两个三角形,若把这两个三角形拼成一个平
面四边形,则能拼出中心对称图形 个.
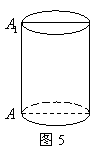 |
15.如图5,有一木质圆柱形笔筒的高为![]() ,底面半径为
,底面半径为![]() ,现要围绕笔筒的
,现要围绕笔筒的
表面由![]() 至
至![]() (
(![]() 在圆柱的同一轴截面上)镶入一条银色金属线作为装
在圆柱的同一轴截面上)镶入一条银色金属线作为装
饰,这条金属线的最短长度是 .
三、解答下列各题:本题有10小题,共75分.解答应写出文字说明、推理过程或演算步骤.
16.本题满分6分.
计算:![]() .
.
17.本题满分6分.
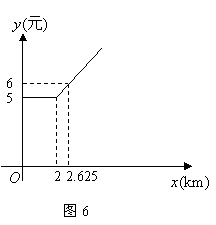
在市区内,我市乘坐出租车的价格![]() (元)与路程
(元)与路程![]() (km)的函数关系图象如图6所示.
(km)的函数关系图象如图6所示.
(1)请你根据图象写出两条信息;
(2)小明从学校出发乘坐出租车回家用了13元,求学校离小明家的路程.
 |
18.本题满分6分.
计算:![]() .
.
19.本题满分6分.
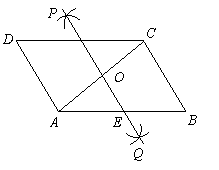
如图7,![]() 是平行四边形
是平行四边形![]() 的对角线.
的对角线.
(1)请按如下步骤在图7中完成作图(保留作图痕迹):
①分别以![]() 为圆心,以大于
为圆心,以大于![]() 长为半径画弧,弧在
长为半径画弧,弧在![]() 两侧的交点分别为
两侧的交点分别为![]() ;
;
②连结![]() 分别与
分别与![]() 交于点
交于点![]() .
.
 (2)求证:
(2)求证:![]() .
.
20.本题满分7分.
甲、乙两位同学本学年11次数学单元测验成绩(整数)的统计如图8所示:
(1)分别求他们的平均分;
(2)请你从中挑选一人参加数学“学用杯”竞赛,并说明你挑选的理由.
 |
21.本题满分7分.
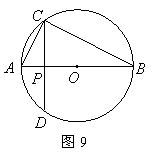
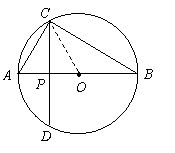
如图9,点![]() 在以
在以![]() 为直径的
为直径的![]() 上,
上,![]() 于
于![]() ,设
,设![]() .
.
(1)求弦![]() 的长;
的长;
(2)如果![]() ,求
,求![]() 的最大值,并求出此时
的最大值,并求出此时![]() 的值.
的值.
 |
22.本题满分8分.
 已知二次函数图象的顶点是
已知二次函数图象的顶点是![]() ,且过点
,且过点![]() .
.
(1)求二次函数的表达式,并在图10中画出它的图象;
(2)求证:对任意实数![]() ,点
,点![]() 都不在这个
都不在这个
二次函数的图象上.
23.本题满分8分.
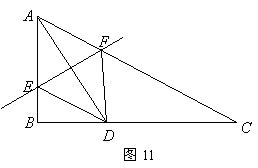
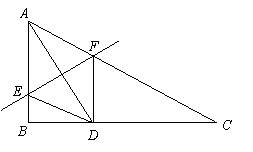
如图11,![]() 中,
中,![]() ,
,![]() 分别在
分别在![]() 上,沿
上,沿![]() 对折,使点
对折,使点![]() 落在
落在![]() 上的点
上的点![]() 处,且
处,且![]() .
.
(1)求![]() 的长;
的长;
(2)判断四边形![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
 |
24.本题满分10分.
梅林中学租用两辆小汽车(设速度相同)同时送1名带队老师及7名九年级的学生到县城参加数学竞赛,每辆限坐4人(不包括司机).其中一辆小汽车在距离考场15km的地方出现故障,此时离截止进考场的时刻还有42分钟,这时唯一可利用的交通工具是另一辆小汽车,且这辆车的平均速度是60km/h,人步行的速度是5km/h(上、下车时间忽略不计).
(1)若小汽车送4人到达考场,然后再回到出故障处接其他人,请你能过计算说明他们能否在截止进考场的时刻前到达考场;
(2)假如你是带队的老师,请你设计一种运送方案,使他们能在截止进考场的时刻前到达考场,并通过计算说明方案的可行性.
25.本题满分11分.
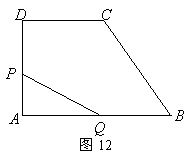
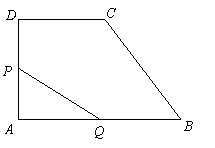
如图12,直角梯形![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向移动,动点
方向移动,动点![]() 从点
从点![]() 出发,在
出发,在![]() 边上移动.设点
边上移动.设点![]() 移动的路程为
移动的路程为![]() ,点
,点![]() 移动的路程为
移动的路程为![]() ,线段
,线段![]() 平分梯形
平分梯形![]() 的周长.
的周长.
(1)求![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的取值范围;
的取值范围;
(2)当![]() 时,求
时,求![]() 的值;
的值;
 (3)当
(3)当![]() 不在
不在![]() 边上时,线段
边上时,线段![]() 能否平分梯形
能否平分梯形![]() 的面积?若能,求出此时
的面积?若能,求出此时![]() 的值;若不能,说明理由.
的值;若不能,说明理由.
数学试卷参考答案与评分意见
一、选择题:每小题3分,共15分.每小题给出四个答案,其中有一个是正确的,把所选答案的编号填写在题目后面的括号内.
1.C; 2.C; 3.C; 4.A; 5.B.
二、填空题:每小题3分,共30分.答案填在横线上.
6.![]() 7.
7.![]() 8.
8.![]() 9.
9.![]() 10.
10.![]() 11.
11.![]() 12.
12.![]()
13.![]() 14.
14.![]() 15.
15.![]()
三、解答下列各题:本题有10小题,共75分.解答应写出文字说明、推理过程或演算步骤.
16.本题满分6分
解:原式![]() ····················································································· 4分
····················································································· 4分
![]() .······································································································ 6分
.······································································································ 6分
17.本题满分6分
解:(1)在0到2km内都是5元;2km后,每增加0.625km加1元.····················· 2分
(答案不唯一)
(2)设射线的表达式为![]() .依题意,得
.依题意,得
![]() 解得:
解得:![]() .得
.得![]() .·································· 5分
.·································· 5分
将![]() 代入上式,得
代入上式,得![]() .
.
所以小明家离学校7km.························································································ 6分
18.本题满分6分.
解:原式![]() ························································ 4分
························································ 4分
![]() ······························································································ 5分
······························································································ 5分
![]() .······································································································· 6分
.······································································································· 6分
 19.本题满分6分.
19.本题满分6分.
(1)作图如右······························································· 2分
(2)证明:根据作图知,![]() 是
是![]() 的垂直平分线,··· 3分
的垂直平分线,··· 3分
所以![]() ,且
,且![]() .
.
因为![]() 是平行四边形,所以
是平行四边形,所以![]() .···· 4分
.···· 4分
所以![]() .············································· 5分
.············································· 5分
所以![]() .··························································· 6分
.··························································· 6分
20.本题满分7分.
解:(1)![]() .
.
![]() .······························ 4分
.······························ 4分
(2)应选甲同学参加比赛.因为甲超过平均分的次数比乙多,比乙更容易获得高分
(也可以从众数等方面去说明).············································································· 7分
(选乙时,分析图形直接得出或通过计算方差等说明乙的稳定性比甲好,也给满分)
 21.解:(1)连结
21.解:(1)连结![]() ,··············· 2分
,··············· 2分
所以![]() ,······ 3分
,······ 3分
得![]() .
.
(也可以根据![]() 求解)··································································· 4分
求解)··································································· 4分
(2)由于![]() ,所以
,所以![]() ,················································ 5分
,················································ 5分
得![]() ,所以
,所以![]() 的最大值为25,此时
的最大值为25,此时![]() .·········································· 7分
.·········································· 7分
22.本题满分8分.
解:(1)依题意可设此二次函数的表达式为![]() ,····························· 2分
,····························· 2分
又点![]() 在它的图象上,可得
在它的图象上,可得![]() ,解得
,解得![]() .·································· 3分
.·································· 3分
所求为![]() .·················································································· 4分
.·················································································· 4分
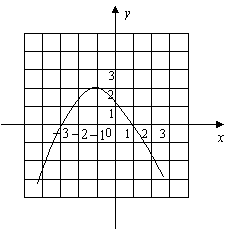 令
令![]() ,得
,得![]()
画出其图象如右.·················································· 5分
(2)证明:若点![]() 在此二次函数的图象上,
在此二次函数的图象上,
则![]() .
.
得![]() .·············································· 7分
.·············································· 7分
方程的判别式:![]() ,该方程无解.
,该方程无解.
 所以原结论成立.·················································· 8分
所以原结论成立.·················································· 8分
23.本题满分8分.
解:(1)因为![]() ,
,
所以![]() 是直角三角形,
是直角三角形,![]() ,
,
又![]() ,所以
,所以![]() ···· 2分
···· 2分
由![]() ,得
,得![]() ,·········································································· 3分
,·········································································· 3分
又![]() ,所以
,所以![]() ,所以
,所以![]() ,························· 4分
,························· 4分
所以![]() ,得
,得![]() .······························································ 5分
.······························································ 5分
(2)四边形![]() 是菱形.················································································· 6分
是菱形.················································································· 6分
证明:由(1)知,![]() ,所以
,所以![]() 是平行四边形,············· 7分
是平行四边形,············· 7分
又![]() ,所以四边形
,所以四边形![]() 是菱形.··························································· 8分
是菱形.··························································· 8分
24.本题满分10分.
解:(1)![]() (分钟),
(分钟),![]() ,
,
![]() 不能在限定时间内到达考场.············································································· 4分
不能在限定时间内到达考场.············································································· 4分
(2)方案1:先将4人用车送到考场,另外4人同时步行前往考场,汽车到考场后返回到与另外4人的相遇处再载他们到考场.···················································································································· 5分
先将4人用车送到考场所需时间为![]() (分钟).
(分钟).
0.25小时另外4人步行了1.25km,此时他们与考场的距离为![]() (km)
(km)
······························································································································ 7分
设汽车返回![]() 后先步行的4人相遇,
后先步行的4人相遇,
![]() ,解得
,解得![]() .
.
汽车由相遇点再去考场所需时间也是![]() .······················································· 9分
.······················································· 9分
所以用这一方案送这8人到考场共需![]() .
.
所以这8个个能在截止进考场的时刻前赶到.······················································· 10分
方案2:8人同时出发,4人步行,先将4人用车送到离出发点![]() 的
的![]() 处,然后这4个人步行前往考场,车回去接应后面的4人,使他们跟前面4人同时到达考场.···························································· 6分
处,然后这4个人步行前往考场,车回去接应后面的4人,使他们跟前面4人同时到达考场.···························································· 6分
由![]() 处步行前考场需
处步行前考场需![]() ,
,
汽车从出发点到![]() 处需
处需![]() 先步行的4人走了
先步行的4人走了![]() ,
,
设汽车返回![]() (h)后与先步行的4人相遇,则有
(h)后与先步行的4人相遇,则有![]() ,解得
,解得![]() ,
,
······························································································································ 8分
所以相遇点与考场的距离为![]() .
.
由相遇点坐车到考场需![]() .
.
所以先步行的4人到考场的总时间为![]() ,
,
先坐车的4人到考场的总时间为![]() ,
,
他们同时到达,则有![]() ,解得
,解得![]() .
.
将![]() 代入上式,可得他们赶到考场所需时间为
代入上式,可得他们赶到考场所需时间为![]() (分钟).
(分钟).
![]() .
.
![]() 他们能在截止进考场的时刻前到达考场.·························································· 10分
他们能在截止进考场的时刻前到达考场.·························································· 10分
其他方案没有计算说明可行性的不给分.
25.本题满分11分.
解:(1)过![]() 作
作![]() 于
于![]() ,则
,则![]() ,可得
,可得![]() ,
,
所以梯形![]() 的周长为18.·············································································· 1分
的周长为18.·············································································· 1分
![]() 平分
平分![]() 的周长,所以
的周长,所以![]() ,····························································· 2分
,····························································· 2分
 因为
因为![]() ,所以
,所以![]() ,
,
所求关系式为:![]() .·············· 3分
.·············· 3分
(2)依题意,![]() 只能在
只能在![]() 边上,
边上,![]() .
.
![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,得··························· 4分
,得··························· 4分
![]() ,即
,即![]() ,
,
解方程组![]() 得
得![]() .··················································· 6分
.··················································· 6分
(3)梯形![]() 的面积为18.············································································· 7分
的面积为18.············································································· 7分
当![]() 不在
不在![]() 边上,则
边上,则![]() ,
,
(![]() )当
)当![]() 时,
时,![]() 在
在![]() 边上,
边上,![]() .
.
如果线段![]() 能平分梯形
能平分梯形![]() 的面积,则有
的面积,则有![]() ········································· 8分
········································· 8分
可得:![]() 解得
解得![]() (
(![]() 舍去).·········································· 9分
舍去).·········································· 9分
(![]() )当
)当![]() 时,点
时,点![]() 在
在![]() 边上,此时
边上,此时![]() .
.
如果线段![]() 能平分梯形
能平分梯形![]() 的面积,则有
的面积,则有![]() ,
,
可得![]() 此方程组无解.
此方程组无解.
所以当![]() 时,线段
时,线段![]() 能平分梯形
能平分梯形![]() 的面积.········································· 11分
的面积.········································· 11分