中考数学系统复习函数与图象测试
《函数与图象》测试题
姓名___________ 班级___________ 分数___________
一、选择题（10×3′=30′）（请将你认为正确的选项写在题号下的空格中）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1、点 P（a，a－2）在第四象限，则 a 的取值范围是（ ）
A、－2＜a＜0 B、0＜a＜2 C、a＞2 D、a＜0
2、弹簧的长度与所挂物体的质量的关系为一次函数，其图象如右图所示，则不挂物体的弹簧长度是（ ）A、10cm B、8cm C、5cm D、7cm
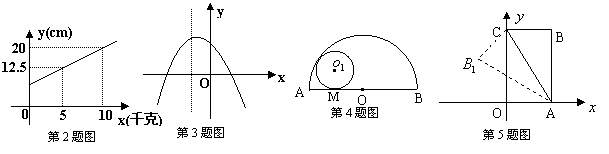
3、已知 y＝ax2＋bx＋c 的图像如图所示，则 a、b、c 满足（ ）
A、a＜0，b＜0，c＜0 B、a＞0，b＜0，c＞0
C、a＜0，b＞0，c＞0 D、a＜0，b＜0，c＞0
4、如图,半圆O的直径AB=4,与半圆O内切的⊙O1与AB切于点M,设⊙O1的半径为
，AM=
，则关于的函数关系式是（ ）
A、
B、
C、
D、
5、在直角坐标系中，将矩形OABC沿AC对折,使点B落在点
处,已知
，点
，则点的坐标为（ ）
A、（-，） B、（-，） C、（-，） D、（-，）
6、在函数 y＝
（k＜0）的图象上有A（1，y1）、B（－1，
）、C（－2，
）三个点，则下列各式中正确（ ）
A、y1＜y2＜y3 B、y1＜y3＜y2 C、y3＜y2＜y1 D、y2＜y3＜y1
7、抛物线 y＝－x2 不具有的性质是（ ）
A、开口向下 B、对称轴是 y 轴 C、与 y 轴不相交 D、最高点是原点
8、抛物线 y＝x2－4x＋c 的顶点在 x 轴，则 c 的值是（ ）
A、0 B、4 C、－4 D、2
9、已知 k1＜0＜k2，则函数
y＝k1x 和 y＝
的图象大致是（ ）
 |
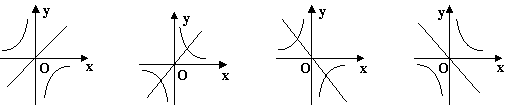A B C D
10、某二元一次方程的解是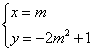
，若把看作平面直角坐标系中的横坐标,看作平面坐标系中的纵坐标,下面说法正确的是（ ）
A、点
一定不在第一象限 B、点一定不在坐标原点
C、随的增大而增大
D随的增大而减小
二、填空题（8×3′=24′）
11、某书定价 8 元，如果购买 10本以上，超过 10 本的
部分打八折。请写出购买数量 x（本）（x>10且为整数）与
付款金额 y（元）之间的关系式___________.
12、若正比例函数
与
的图象关于轴对称,则
的值=___________.
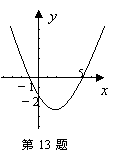
13、已知二次函数
的图象如图,则下列结论：①a，b同号；②当
时,函数值相等；③
；④当
时,的值只能取零.其中正确的是___________.
14、函数
中，自变量的取值范围是___________.
15、在平面直角坐标系中,入射光线经过轴上的点A（0，3），由轴上的点C反射,反射光线经过点B（－3，1），则点C的坐标为___________.
16、请你选择一组喜欢的a、b、c的值,使二次函数的图象同时满足下列条件：①开口向下；②当
时,随的增大而增大，当
时,随的增大而减小；这样的二次函数的解析式可以是____________________.
17、一辆高为4米,宽为2米的货车,通过截面为抛物线
的隧道,则抛物线中的
的取值范围是___________.
18、已知抛物线
的对称轴是
,开口方向和形状与抛物线
相同,且经过原点,则a=_____，b=_____，c=______.
三、解答题（19、20、21每题各10分,22、23、24每题各12分,共66分）
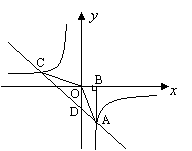19、如图,直角△ABO的顶点A是双曲线
与
在第四象限的交点,AB⊥轴于B点,且
.（1）求这两个函数的解析式；（2）求直线与双曲线的两个交点A、C的坐标及△AOC的面积.
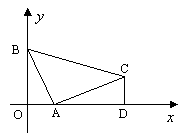
20、如图,已知直线
分别与轴、轴交于点A、B,以线段AB为直角边在第一象限内作等腰Rt△ABC，∠BAC=90°，过C作CD⊥轴于D.（1）求点A、B的坐标和AD的长；（2）求过B、A、C三点的抛物线的解析式.
 |
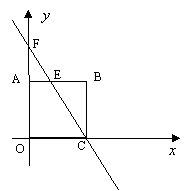21、如图,在平面直角坐标系中,正方形AOCB的边长为6,O为坐标原点,边OC在轴的正半轴上,边OA在轴的正半轴上,E为边AB上一点,直线EC交轴于F,且
∶
1∶3.（1）求出点E的坐标；（2）求直线EC的函数解析式.
22、今年6月份,我市某果农收获荔枝30吨,香蕉13吨,现计划租用甲、乙两种货车共10辆将这批水果全部运往深圳,已知甲种货车可装荔枝4吨和香蕉1吨；乙种货车可装荔枝、香蕉各2吨.（1）该果农安排甲、乙两种货车时有几种方案?请你帮助设计出来.（2）若甲种货车每辆要付运输费2000元,乙种货车每辆要付运输费1300元,则该果农应选择哪种方案使运费最少?最少运费是多少元?
|
| 25 | 30 | 40 | … |
|
| 25 | 20 | 10 | … |
23、某产品每件成本价20元,试销阶段产品的月销售量（件）与每件产品的销售价（元）之间的关系如下表：
（1）若日销售量（件）是每件产品的销售价（元）
的一次函数,求日销售量（件）与每件产品的销售价（元）之间的函数关系式；（2）要使日销售利润W（元）最大,每件产品的销售价（元）应定为多少?此时每日销售利润是多少?
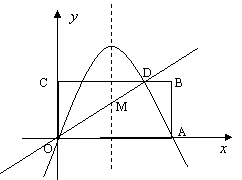24、矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A（6，0），C（0，3）,直线
与BC边相交于点D,（1）求点D的坐标；（2）若抛物线y=
经过D、A两点,试确定此抛物线的表达式；（3）设在（2）中抛物线的对称轴与直线OD交于M，点Q为对称轴上一动点,以Q、O、M为顶点的三角形与
相似,求符合条件的Q点的坐标.
四、（本题由19——24题各减2分，共12分）（实验班必做,普通班选做）
如图，在平面直角坐标系内，⊙C与y轴相切于D点，与x轴相交于A（2，0）、B（8，0）两点，圆心C在第四象限.
⑴ 求点C的坐标；
⑵ 连结BC并延长交⊙C于另一点E，若线段BE上有一点P，使得AB2＝BP·BE，能否推出AP⊥BE？请给出你的结论，并说明理由；
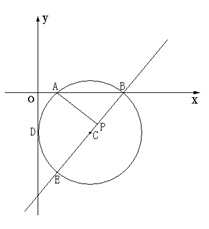⑶ 在直线BE上是否存在点Q，使得AQ2＝BQ·EQ？若存在，求出点Q的坐标；若不存在，也请说明理由.