提高测试
（一）判断题（每小题1分，共6分）：
1．经过一点可以画无数条直线，经过两点可以画一条直线，经过三点可以画三条直线
………………………………………………………………………………………（ ）
【提示】错的是第三句话，因为三点可在一条直线上，也可不在一条直线上，当三点在一条直线上时（我们称之三点共线），经过这三点只可以画一条直线．
【答案】×．
2．两条直线如果有两个公共点，那么它们就有无数个公共点…………………（ ）
【提示】两点确定唯一的直线．
【答案】√．
3．射线AP与射线PA的公共部分是线段PA……………………………………（ ）
【提示】线段是射线的一部分．
【答案】如图：
显然这句话是正确的．
4．线段的中点到这条线段两端点的距离相等……………………………………（ ）
【提示】两点的距离是连结两点的线段的长度．
【答案】√．
5．有公共端点的两条射线叫做角…………………………………………………（ ）
【提示】角是有公共端点的两条射线组成的图形．
【答案】×．
6．互补的角就是平角………………………………………………………………（ ）
【提示】如图，射线OA绕点O旋转，当终止位置OC和起始位置OA成一直线时，所成的角叫平角．平角是一个量数为180°的角．
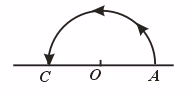
【答案】×．
【点评】互补两角的和是180°，平角为180°．就量数来说，两者是相同的，但从“形”上说，互补两角不一定有公共顶点，故不一定组成平角．所以学习概念时，一定要注意区别它们的不同点，以免混淆．
二．填空题（每小题2分，共16分）：
7．如图，图中有________条直线，有________条射线，有________条线段，以E为顶点的角有________个．
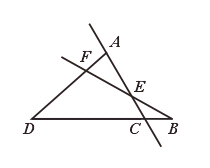
【提示】直线没有端点，可向两方无限延伸．射线有一个端点，可向一方无限延伸，线段有两个端点，不延伸．直线上一点将一条直线分成两条射线．直线上两点和它们之间的部分是线段．
【答案】1，9，12，4．
12条线段分别是：线段AF、AD、FD、DC、DB、CB、BE、BF、EF、CE、CA、EA．
8．如图，点Ｃ、D在线段AB 上．AC＝6 cm，CD＝4 cm，AB＝12 cm，则图中所有线段的和是________cm．
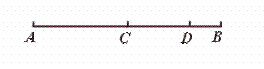
【提示】1．数出图中所有的线段；2．算出不同线段的长度；3．将所有线段的长度相加，得和．
【答案】40．
9．线段AB＝12.6 cm，点C 在BA 的延长线上，AC＝3.6 cm，M 是BC 中点，则AM 的长是________cm．
【提示】画出符合题意的图形，以形助思．
【答案】4.5．
∵ BC＝AB＋AC，M是BC中点，
∴ AM＝CM－AC
＝
BC－AC
＝（AB＋AC）－AC
＝（AB－AC）
＝（12.6－3.6）
＝4.5（cm）．
【点评】在进行线段长度计算时，可是对其表达式进行变形、最后将值代入，求出结果．这样可简化计算，提高正确率．
10．如图，∠AOB＝∠COD＝90°，∠AOD＝146°，则∠BOC＝________°．
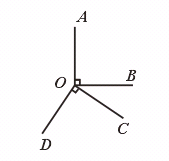
【提示】∠BOC＝360°－∠AOB －∠AOD －∠DOC．
【答案】34．
11．如图，OB 平分∠AOC．且∠2∶∠3∶∠4＝3∶5∶4，则∠2＝________°，
∠3＝________°，∠4＝________°．
【提示】1周角＝360°．设1份为x°，列方程求解．
【答案】72；120；96．
12．∠A与∠B互补，∠A与∠C互余，则2∠B－2∠C＝________°．
【提示】∠A＋∠B＝180°．∠A＋∠C＝90°．代入要求的式子，化简即得．
【答案】180°．
∵ ∠A＋∠B＝180°，∠A＋∠C＝90°，
∴ ∠B＝180°－∠A．
∴ 2∠B－2∠C＝2（180°－∠A）－2∠C
＝360°－2∠A－2∠C
＝360°－2（∠A＋∠C）
＝360°－2×90°
＝180°．
【点评】由已知可得关于∠A、∠B、∠C的方程组
，此时不能确定
∠B、∠C的大小，但只要将两式的两边分别相减，使得∠B－∠C＝90°，2∠B－2∠C便不难求得．这种整体代入的思想是求值题中常用的方法．
13．已知：∠
的余角是52°38′15″，则∠ 的补角是________．
【提示】分步求解：先求出∠ 的度数，再求∠ 的补角的度数．
【答案】142°38′15″．
∵ ∠的余角是52°38′15″，
∴ ∠＝90°－52°38′15″
＝89°59′60″－52°38′15″
＝37°21′45″．
∴ ∠的补角＝180°－37°21′45″
＝179°59′60″－37°21′45″
＝142°38′15″．
【点评】题中∠a 只起过渡作用，可考虑到而不求，作整体代入．
∵ ∠a ＝ 90°－52°38′15″，
∴ ∠a 的补角＝180°－∠a
＝180°－（90°－52°38′15″）
＝90°＋52°38′15″
＝142°38′15″．
这样避开了单位换算，利于提高运算速度及正确率．
若将已知条件反映到如图所示的图形上，运用数形结合的思想观察图形，则一目了然．一般地，已知∠a 的余角，求∠a 的补角，则∠a 的补角＝90°＋∠a 的余角，即任一锐角的补角比它的余角大90°．利用这个结论解该题就更准确、快捷．
14．由2点30分到2点55分，时钟的时针旋转了________度，分针旋转了________度，此刻时针与分针的夹角是________度．
【提示】分针1小时旋转360°，1分旋转6°，时钟1小时旋转30°，1分旋转0.5°．
【答案】12.5，150，117.5．
（三）选择题（每小题3分，共24分）
15．已知线段AB＝10 cm，AC＋BC＝12 cm，则点C 的位置是在：①线段AB 上；②线段AB 的延长线上；③线段BA 的延长线上；④直线AB 外．其中可能出现的情况有………………………………………………………………………………（ ）
（A）0种 （B）1种 （C）2种 （D）3种
【提示】用数形结合的方式考虑．
【答案】D．
若点C在线段AB上，如下图，则AC＋BC＝AB＝10 cm．与AC＋BC＝12 cm不合，故排除①．
若点C 在线段AB 的延长线上，如下图，AC＝11 cm，BC＝1 cm，则AC＋BC＝
11＋1＝12（cm），符合题意．
若点C 在线段BA 的延长线上，如下图，AC＝1 cm，BC＝11 cm，则AC＋BC＝
1＋11＝12（cm），符合题意．
若点C在直线AB外，如下图，则AC＋BC＝12（cm），符合题意．
综上所述：可能出现的情况有3种，故选D．
16．分别在线段MN的延长线和MN的反向延长线上取点P、Q，使MP＝2NP．MQ＝2MN．则线段MP 与NQ 的比是…………………………………………（ ）
（A）
（B）
（C） （D）
【提示】根据条件画出符合题意的图形，以形助思．
【答案】B．
根据题意可得下图：
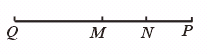
解法一：
∵ MP＝2NP，
∴ N是MP的中点．
∴ MP＝2MN．
∵ MQ＝2MN，
∴ NQ＝MQ＋MN＝2MN＋MN＝3MN．
∴ MP∶NQ＝2MN∶3MN＝2∶3＝．
解法二：
设MN＝x．
∵ MP＝2NP，
∴ N是MP的中点．
∴ MP＝2MN＝2x．
∵ MQ＝2MN＝2x，
∴ NQ＝MQ＋MN＝2MN＋MN＝3MN＝3x．
∴ MP∶NQ＝2MN∶3MN＝2 x∶3 x＝．
故选B．
17．一条直线可以将平面分成两部分，两条直线最多可以将平面分成四部分，三条直线最多可以将平面分成n 部分，则n 等于………………………………………（ ）
（A）6 （B）7 （C）8 （D）9
【提示】画图探索．
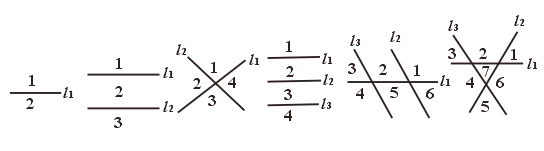
一条线 两条直线 三条直线
【答案】B．
【点评】平面内一条直线将平面分成两部分，记作a1＝1＋1＝2；
平面内两条直线将平面最多分成四部分，记作a2＝1＋1＋2＝4；
平面内三条直线将平面最多分成七部分，记作a3＝1＋1＋2＋3＝7；
平面内四条直线将平面最多分成几部分？由图可知，共可分成11个部分，记作a4＝1＋1＋2＋3＋4＝11．
若平面上有n条直线，最多可将平面分成多少部分，此时n条直线的相对位置如何？
从前面的分析不难推出平面上有n 条直线时，最多可将平面分成an＝1＋1＋2＋3＋4＋…＋n＝1＋
＝
个部分，此时每两条直线都相交，且没有三条直线交于一点．
18．若互补两角有一条公共边，则这两个角的平分线所组成的角………………（ ）
（A）一定是直角 （B）一定是锐角
（C）一定是钝角 （D）是直角或锐角
【提示】分两种情况：①互补两角有公共顶点，有一条公共边没有重叠部分；②互补两角有公共顶点有一条公共边有重叠部分．
【答案】D．
如图：
19．已知 、
都是钝角，甲、乙、丙、丁四人计算
的结果依次是30°、
35°、60°、75°，其中恰有正确结果．这个正确结果是…………………（ ）
（A）30° （B）35° （C）60° （D）75°
【提示】列不等式求解．
【答案】C．
∵ 、都是钝角，
∴ 180°＜
＜360°．
∴ 36°＜
＜72°．
∵ 30°、35°、75°都不在此等圆内，仅60°属此等圆．
∴ 选C．
20．如图，∠AOB＝∠BOC＝∠COD＝∠DOE＝30°．图中互补的角有……（ ）
（A）10对 （B）4对 （C）3对 （D）4对
【提示】两个角的和为180°，这两个角叫互为补角．补角的概念仅与角的大小有关而与角的位置无关．
【答案】B．
原因如下：
∵ ∠AOB＝∠BOC＝∠COD＝∠DOE＝30°
∴ ∠AOE＋∠AOC＝120°＋60°＝180°，
∠AOE＋∠BOD＝120°＋60°＝180°，
∠AOE＋∠COE＝120°＋60°＝180°，
∠AOD＋∠BOE＝90°＋90°＝180°．
∴ ∠AOE 与∠AOC、∠AOE 与∠BOD、∠AOE 与∠COE、∠AOD 与∠BOE 是4对互补的角．
21．∠1、∠2互为补角，且∠1＞∠2，则∠2的余角是…………………………（ ）
（A）
（B）∠1 （C）
（D）∠2
【提示】将已知条件反映到图形上，运用数形结合的方法观察图形，便知结果，或根据互补、互余的定义进行推理．
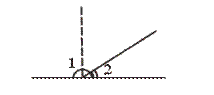
【答案】C．
由图可知：
∠2的余角
＝∠1－90°
＝∠1－
＝∠1－∠1－∠2
＝．
或：
∵ ∠1、∠2互为补角，
∴ ∠1＋∠2＝180°．
∴ ∠2的余角
＝90°－∠2
＝－∠2
＝∠1＋∠2－∠2
＝．
故选C．
22．设时钟的时针与分针所成角是a ，则正确的说法是………………………（ ）
（A）九点一刻时，∠a 是平角 （B）十点五分时，∠a 是锐角
（C）十一点十分时，∠a 是钝角 （D）十二点一刻时，∠a 是直角
【提示】时钟的时针1小时转30°，1分转0.5°；分针1小时转360°，1分转6°，还可画图，以形助思．
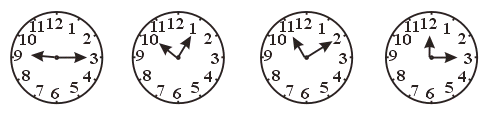
【答案】B．
（四）计算题（每小题3分，共9分）
23．118°12′－37°37′×2．
【提示】先算乘，再求差．
【答案】42°58′．
计算过程如下：
118°12′－37°37′×2
＝118°12′－75°14′
＝117°72′－75°14′
＝42°58′．
24．132°26′42″－41.325°×3．
【提示】将132°26′42″化成以“度”为单位的量再计算；
或将41.325°×3的积化成“度”、“分”、“秒”后再算．
【答案】解法一 132°26′42″－41.325°×3
＝132.445°－123.975°
＝8.47°．
解法二 132°26′42″－41.325°×3
＝132°26′42″－123.975°
＝132°26′42″－123°58′30″
＝131°86′42″－123°58′30″
＝8°28′12″．
【点评】在“度”、“分”、“秒”的混合运算中，若将“分”、“秒”化成度，则可将“度”“分”“秒”的计算转化成小数运算，免去繁杂的“进位”或“退位”．提高运算速度和正确率．
25．360°÷7（精确到分）．
【提示】按四舍五入取近似值，满30″或超过30″即可进为1″．
【答案】约为51°26′．
计算过程如下：
360°÷7
＝51°＋3°÷7
＝51°＋25′＋5′÷7
＝51°＋25′＋300″÷7
≈51°＋25′＋43″
≈51°26′．
（五）画图题（第26小题4分，第27小题5分，第28小题6分，共15分）
26．已知：线段a、b、c（b＞c），画线段AB，使AB＝2a－（b－c）．
【提示】AB＝2a－（b－c）＝2a＋c－b．
【答案】方法一：
量得 a＝20 mm，b＝28 mm，c＝18 mm．
AB＝2a－（b－c）
＝2×20－（28－18）
＝40－5
＝35（mm）．
画线段AB＝35 mm（下图），
则线段AB就是所要画的线段．
方法二：
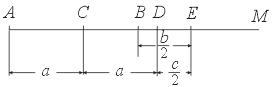
画法如下（如上图）：
（1）画射线AM．
（2）在射线AM上依次截取AC＝CD＝a，DE＝c．
（3）在线段EA上截取EB＝b．
则线段AB就是所要画的线段．
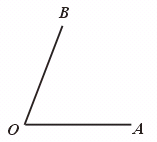
27．已知∠a ，∠b
，∠g ，画∠AOB，使∠AOB＝2∠a＋∠b－∠g ．
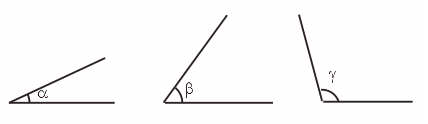
【提示】方法一：先量、后算、再画；
方法二：叠加法，逐步画出．
【答案】方法一：
量得∠a ＝25°，∠b ＝54°，∠g ＝105°，
∠AOB＝2∠a ＋∠b －∠g
＝2×25°＋54°－×105°
＝50°＋54°－35°
＝69°．
画∠AOB＝69°，则∠AOB就是所要画的角．
方法二：
画法：
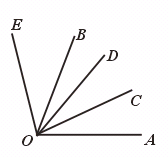
（1）画∠AOC＝∠a ，
（2）以O为顶点，OC为一边在∠AOC的外部画∠COD＝∠a ．
（3）以O为顶点，OD为一边在∠AOD的外部画∠DOE＝∠b ．
（4）以O为顶点，OE为一边在∠EOA的内部画∠EOB＝∠g ．
则∠AOB就是所要画的角．
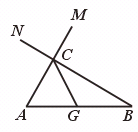
28．读句画图，填空：
（1）画线段AB＝40 mm；
（2）以A为顶点，AB为一边，画∠BAM＝60°；
（3）以B为顶点，BA为一边，在∠BAM的同侧画∠ABN＝30°，AM与BN相交于点C；
（4）取AB的中点G，连结CG；
（5）用量角器量得∠ACB＝______度；
（6）量得CG的长是_____mm，AC的长是_____mm，图中相等的线段有________．
【提示】按语句的顺序，抓住概念用语（如线段、角等）和位置术语（如以……为顶点，在……同侧等）依次画图．
【答案】90，20，20．
AC＝CG＝AG＝BG．
（六）解答题（每小题5分，共30分）
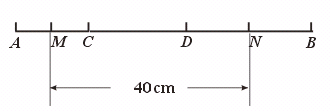
29．如图，线段AB被点C、D分成了3︰4︰5三部分，且AC的中点M和DB的中点N之间的距离是40 cm，求AB的长．
【提示】引入未知数，列方程求解．
【答案】60 cm．
设一份为x cm，则AC＝3 x cm，CD＝4 x cm，DB＝5 x cm．
∵ M是AC的中点，
∴ CM＝AC＝
x cm．
∵ N是DB的中点，
∴ DN＝DB＝
x cm．
∵ MN＝MC＋CD＋DN，
又 MN＝40 cm，
∴ x＋4 x＋x＝40，
8x＝40．
∴ x＝5．
∴ AB＝AC＋CD＋DB＝12 x＝12×5＝60（cm）．
30．一个角的补角与20°角的和的一半等于这个角的余角的3倍，求这个角．
【提示】两角互余和为90°，两角互补和为180°．设这个角为x°，列方程求解．
【答案】68°．
设这个角为x°，根据题意得
（180°－x＋20°）＝3（90°－x），
100°－x＝270°－3 x，
x＝170°，
∴ x＝68°，
即这个角为68°．
31．如图，直线AB、CD相交于点O，OB平分∠EOD，∠COE＝100°，求∠AOD和∠AOC的度数．
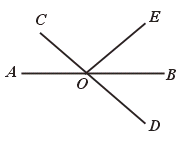
【提示】由∠COE＝100°，OB平分∠EOD，可求出∠BOD的度数，进而求出∠AOD和∠AOC的度数．
【答案】∠AOD＝140°，∠AOC＝40°．
计算过程如下：
∵ ∠COD＝180°，∠COE＝100°（已知），
∴ ∠EOD＝∠COD－∠COE＝180°－100°＝80°．
∵ OB平分∠EOD（已知），
∴ ∠BOD＝∠EOD＝×80°＝40°（角平分线定义）．
∵ ∠AOB＝180°（平角定义），
∴ ∠AOD＝∠AOB－∠BOD＝180°－40°＝140°，
∠AOC＝∠COD－AOD＝180°－140°＝40°．
【点评】由计算可知，∠BOC＝∠COE＋∠EOB＝100°＋40°＝140°．
∴ ∠AOD＝∠BOC，又知∠AOC＝∠BOD，这是一种偶然的巧合，还是必然的结果？在第二章“相交线、平行线”中可揭开这个谜．
32．如图，∠AOC、∠BOD都是直角，且∠AOB与∠AOD的度数比是2︰11，求∠AOB和∠BOC的度数．
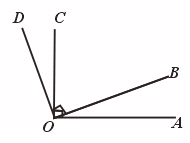
【提示】设∠AOB＝x°，∠BOC＝y°，列方程组求解．
【答案】∠AOB＝20°，∠BOC＝70°．
计算过程如下：
∵ ∠AOC、∠BOD都是直角（已知），
∴ ∠AOB＋∠BOC＝90°，∠COD＋∠BOC＝90°（直角的定义）．
∴ ∠AOB＝∠COD（同角的余角相等）．
设∠AOB＝∠COD＝x° ，∠BOC＝y°．
由题意得
即 
解得
即∠AOB＝20°，∠BOC＝70°．
33．考察队从营地P处出发，沿北偏东60°前进了5千米到达A地，再沿东南方向前进到达C地，C地恰好在P地的正东方向．
（1）按1︰100 000画出考察队行进路线图．
（2）量出∠PAC、∠ACP的度数（精确到1°）．
（3）测算出考察队从A到C走了多少千米？此时他们离开营地多远？（精确到0.1千米）．
【提示】比例尺＝图上距离︰实际距离，先根据1︰100 000的比例尺算出PA的图上距离，然后再画图．
【答案】（1）考察队行进的路线图如右图所示．
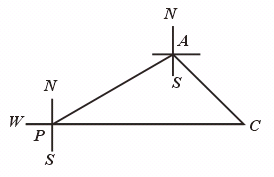
（2）量得∠PAC＝105°，∠ACP＝45°．
（3）算得AC≈3.5千米；PC≈6.8千米．
略解如下：
（1）算出PA的图上距离，由5千米＝500 000厘米．
∴ 
＝
．
∴ PA＝5厘米．
（3）量得AC≈3.5厘米，PC＝6.8厘米．
∴ AC的实际距离约为：3.5厘米×100 000＝350 000厘米＝3.5千米；
PC的实际距离约为：6.8厘米×100 000＝680 000厘米＝6.8千米．
34．已知直角∠AOB，以O为顶点，在∠AOB的内部画出100条射线，则以OA、OB及这些射线为边的锐角共有多少个？若以O为项点，在∠AOB的内部画出几条射线（n≥1的自然数），则OA、OB以及这些射线为边的锐角共有多少个？
【提示】在∠AOB的内部，以O为顶点，画1，2，3，4条射线，数数各有多少个锐角，找出规律，再计算100条射线、n条射线所构成的锐角的个数．
【答案】5 150个锐角；
个锐角．
1条射线 1＋1＝2（个锐角），
2条射线 2＋2＋1＝5（个锐角），
3条射线 3＋3＋2＋1＝9（个锐角），
4条射线 4＋4＋3＋2＋1＝14（个锐角），
……
100条射线 100＋100＋99＋98＋…＋3＋2＋1
＝100＋
＝100＋5 050
＝5 150（个锐角），
n条射线 n＋n＋（n－1）＋（n－2）＋…＋3＋2＋1
＝n＋
＝（个锐角）．
【点评】数锐角的个数与数线段的条数一样，以OA为始边，另一条射线为角的终边依次去数，这样可不遗漏不重复地将要数的锐角个数数准确．注意∠AOB是直角，故这个角不在计数的范围内．
若题目改成：已知∠AOB，以O为顶点，在∠AOB的内部画出n条射线，n为非零自然数，以OA、OB以及这些射线为边的角共有多少个？
答案是：共有
个角．