中考数学统计初步（二）
知识网络
一、反映数据波动大小
二、揭示数据分布规律
一、选择题
1.某工厂为了选拔1名车工参加加工直径为10mm的精密零件的技术比赛，随
机抽取甲、乙两名车工加工的5个零件，现测得的结果如下表，请你用计算器比较S 2甲、
| 甲 | 10.05 | 10.02 | 9.97 | 9.96 | 10 |
| 乙 | 10 | 10.01 | 10.02 | 9.97 | 10 |
S 2乙的大小
A．S 2甲＞S 2乙 B．S 2甲＝S 2乙
C．S 2甲＜S 2乙 D．S 2甲≤S 2乙
2.在一次科技知识竞赛中，两组学生成绩统计如下表，通过计算可知两组的方差为
，
。下列说法：①两组的平均数相同；②甲组学生成绩比乙组学生成绩稳定；③甲组成绩的众数＞乙组成绩的众数；④两组成绩的中位数均为80，但成绩≥80的人数甲组比乙组多，从中位数来看，甲组成绩总体比乙组好；⑤成绩高于或等于90分的人数乙组比甲组多，高分段乙组成绩比甲组好。其中正确的共有（
）.
| 分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
| 人 数 | 甲组 | 2 | 5 | 10 | 13 | 14 | 6 |
| 乙组 | 4 | 4 | 16 | 2 | 12 | 12 | |
A. 2种 B. 3种 C. 4种 D. 5种
3.在统计中，样本的标准差可以反映这组数据的（ ）
A.平均状态 B.分布规律 C.离散程度 D.数值大小
4.甲、乙两名同学在相同条件下各射击5次，命中的环数如下表：那么下列结论正确的是( )
| 甲 | 8 | 5 | 7 | 8 | 7 |
| 乙 | 7 | 8 | 6 | 8 | 6 |
A．甲的平均数是7，方差是1.2 C．甲的平均数是8，方差是1.2
B．乙的平均数是7，方差是1.2 D．乙的平均数是8，方差是0.8
二、填空题
1.甲、乙、丙三台包装机同时分装质量为400克的茶叶.从它们各自分装的
茶叶中分别随机抽取了10盒，测得它们的实际质量的方差如下表所示：
 |
2.甲、乙、丙三台机床生产直径为60mm的螺丝，为了检验产品质量，从三台机床生产的螺丝中各抽查了20个测量其直径，进行数据处理后，发现这三组数据的平均数都是60mm，它们的方差依次为S2甲=0.162，S2乙=0.058，S2丙=0.149.根据以上提供的信息，你认为生产螺丝质量最好的是__ __机床.
3.一组数据：2，-2，0，4的方差是 。
三、解答题
1市体校准备挑选一名跳高运动员参加全市中学生运动会，对跳高运动队的甲、乙两名运动员进行了8次选拔比赛。他们的成绩（单位：m）如下：
甲：1.70 1.65 1.68 1.69 1.72 1.73 1.68 1.67
乙：1.60 1.73 1.72 1.61 1.62 1.71 1.70 1.75
(1)甲、乙两名运动员的跳高平均成绩分别是多少？
(2)哪位运动员的成绩更为稳定？
(3)若预测，跳过1.65m就很可能获得冠军，该校为了获得冠军，可能选哪位运动员参赛？若预测跳过1.70m才能得冠军呢？
【解】（1）
（2）
故甲稳定
（3）可能选甲参加，因为甲8次成绩都跳过1.65m而乙有3次低于1.65m 可能选乙参加，因为甲仅3次超过1.70m，当然学生可以有不同看法只要有道理
2.为了从甲、乙两名学生中选择一人参加电脑知识竞赛，在相同条件下对他们的电脑知识进行了10次测验，成绩如下：(单位：分)
| 甲成绩 | 76 | 84 | 90 | 84 | 81 | 87 | 88 | 81 | 85 | 84 |
| 乙成绩 | 82 | 86 | 87 | 90 | 79 | 81 | 93 | 90 | 74 | 78 |
(1)请完成下表：
|
| 平均数 | 中位数 | 众数 | 方差 | 85分以上的频率 |
| 甲 | 84 | 84 | 14．4 | 0．3 | |
| 乙 | 84 | 84 | 34 |
(2)利用以上信息，请从三个不同的角度对甲、乙两名同学的成绩进行分析．
【解】（1）
|
| 平均数 | 中位数 | 众数 | 方差 | 85分以上的频率 |
| 甲 | 84 | 84 | 84 | 14.4 | 0.3 |
| 乙 | 84 | 84 | 90 | 34 | 0.5 |
(2)甲成绩的众数是84，乙成绩的众数是90，从两人成绩的众数看，乙的成绩较好.
甲成绩的方差是14.4，乙成绩的方差是34，从成绩的方差看，甲的成绩相对稳定．
甲成绩、乙成绩的中位数、平均数都是84，但从85分以上的频率看，乙的成绩较好．
3.张老师为了从平时在班级里数学比较优秀的王军、张成两位同学中选拔一人参加“全国初中数学联赛”，对两位同学进行了辅导，并在辅导期间进行了10次测验，两位同学测验成绩记录如下表：
|
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 | 第9次 | 第10次 |
| 王军 | 68 | 80 | 78 | 79 | 81 | 77 | 78 | 84 | 83 | 92 |
| 张成 | 86 | 80 | 75 | 83 | 85 | 77 | 79 | 80 | 80 | 75 |
利用表中提供的数据，解答下列问题：
| 平均成绩 | 中位数 | 众数 | |
| 王军 | 80 | 79.5 | |
| 张成 | 80 | 80 |
（1）填写完成下表：
（2）张老师从测验成绩记录表中，求得王军10次测验成绩的方差
=33.2，请你帮助张老师计算张成10次测验成绩的方差
；
（3）请你根据上面的信息，运用所学的统计知识，帮助张老师做出选择，并简要说明理由。
| 平均成绩 | 中位数 | 众数 | |
| 王军 | 80 | 79.5 | 78 |
| 张成 | 80 | 80 | 80 |
【解】（1）
（2）＝13 （3）略。
4．某校为选拔参加2005年全国初中数学竞赛的选手，进行了集体培训．在集训期间进行了10次测试，假设其中两位同学的测试成绩如下面的图表所示：
（1）根据图表中所示的信息填写下表：
（2）这两位同学的测试成绩各有什么特点（从不同的角度分别说出一条即可）?
（3）为了使参赛选手取得好成绩，应选谁参加比赛？为什么？
【解】（1）甲的中位数是94.5，乙的众数是99。
（2）学生的回答是多样的（只要学生说的有道理即可）．例如：
甲考试成绩较稳定，因为方差，极差较小（或甲的平均数比乙的平均数高）；乙有潜力，因为乙的最好成绩比甲的最好成绩高等．
（3）10次测验，甲有8次不少于92分，而乙仅有6次，若想获奖可能性较大，可选甲参赛；若想拿到更好的名次可选乙；因为乙有4次在99分以上．
5.甲、乙两位同学五次数学测验成绩如下表：
| 测验(次) | 1 | 2 | 3 | 4 | 5 | 平均数 | 方差 |
| 甲(分) | 75 | 90 | 96 | 83 | 81 | ||
| 乙(分) | 86 | 70 | 90 | 95 | 84 |
请你在表中的空白处填上适当的数，用学到的统计知识对两位同学的成绩进行分析，并写出一条合理化建议．
【解】甲：8 5，5 3．2． 乙：8 5，7 0．4．
从上述数据可以看出，乙同学的数学成绩不够稳定，波动较大，希望乙同学在学习上补缺补漏，加强能力训练．
6.【05黄岗】为选派一名学生参加全市实践活动技能竞赛，A、B两位同学在学校实习基地现场进行加工直径为20mm的零件的测试，他俩各加工的10个零件的相关数据依次如下图表所示（单位：mm）
根据测试得到的有关数据，试解答下列问题：
⑴ 考虑平均数与完全符合要求的个数，你认为 的成绩好些；
⑵ 计算出SB2的大小，考虑平均数与方差，说明谁的成绩好些；
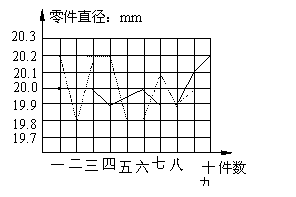⑶ 考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况，你认为派谁去参赛较合适？说明你
的理由。
| 平均数 | 方差 | 完全符合要求个数 | |
| A | 20 | 0.026 | 2 |
| B | 20 | SB2 |
 | |||
 | |||
【解】⑴B
⑵∵
＝0.008 且
，∴
在平均数相同的情况下，B的波动性小，∴B的成绩好些
⑶从图中折线走势可知，尽管A的成绩前面起伏较大，但后来逐渐稳定，误差小，预测A的潜力大，可选派A去参赛
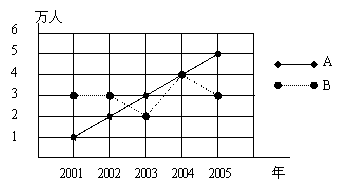
7.【05重庆课改】如图所示，A、B两个旅游点从2001年至2005年“五、一”的旅游
人数变化情况分别用实线和虚线表示．根据图中所示解答以下问题：
（1）B旅游点的旅游人数相对上一年，增长最快的是哪一年？
（2）求A、B两个旅游点从2001到2005年旅游人数的平均数和方差，并从平均数和方
差的角度，用一句话对这两个旅游点的情况进行评价；
（3）A旅游点现在的门票价格为每人80元，为保护旅游点环境和游客的安全，A旅游点
的最佳接待人数为4万人，为控制游客数量，A旅游点决定提高门票价格．已知门票价格x（元）与游客人数y（万人）满足函数关系
．若要使A旅游点的游客人数不超过4万人，则门票价格至少应提高多少？
 |
【解】(1)B旅游点的旅游人数相对上一年增长最快的是2004年．
(2)
＝
＝3（万元）
＝
＝3（万元） 
＝
[(-2)
＋(-1)＋0＋1＋2]＝2
＝[0＋0＋(-1)＋1＋0]＝
从2001至2005年，A、B两个旅游点平均每年的旅游人数均为3万人，
但A旅游点较B旅游点的旅游人数波动大．
(3)由题意，得 ５－
≤４ 解得x≥100 100-80＝20
答：A旅游点的门票至少要提高20元．
选择题、填空题答案
一、选择题 1.A 2.D 3.C 4.A
二、填空题
1. 乙 2. 乙 3. 5