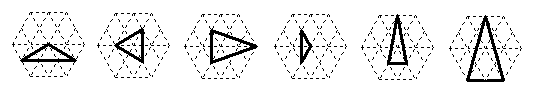中考试题分类汇编—网格
 1.一青蛙在如图8×8的正方形(每个小正方形的边长为1)网格的格点(小正方形的顶点)上跳跃,青蛙每次所跳的最远距离为
1.一青蛙在如图8×8的正方形(每个小正方形的边长为1)网格的格点(小正方形的顶点)上跳跃,青蛙每次所跳的最远距离为![]() ,青蛙从点A开始连续跳六次正好跳回到点A,则所构成的封闭图形的面积的最大值是________.12
,青蛙从点A开始连续跳六次正好跳回到点A,则所构成的封闭图形的面积的最大值是________.12
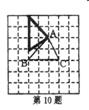
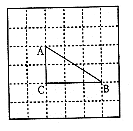
2.如图,在正方形网格上,若使△ABC∽△PBD,则点P应在( C )
A.P1处 B.P2处 C.P3处 D.P4处
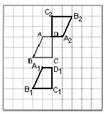
3.在下图的正方形网格中有一个直角梯形ABCD,请你在该图中分别按下列要求画出图形(不要求写出画法):
(1) 把直角梯形ABCD向下平移3个单位得到直角梯形A1B
(2) 将直角梯形ABCD绕点D逆时针旋转180°后得到直角梯形A2B
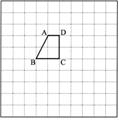
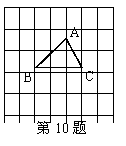
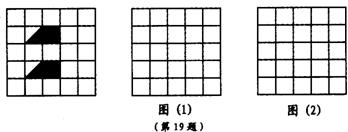
 4.如图,在网格中有一个四边形图案.
4.如图,在网格中有一个四边形图案.
(1)请你画出此图案绕点D顺时针方向旋转900,1800,2700的图案,你会得到一个美丽的图案,千万不要将阴影位置涂错;
(2)若网格中每个小正方形的边长为l,旋转后点A的对应点依次为A1、A2、A3,求四边形AA
(3)这个美丽图案能够说明一个著名结论的正确性,请写出这个结论.
5. 解:(1)如图,正确画出图案
 (2)如图,
(2)如图,![]() =
=![]() -4
-4![]() =(3+5)2-4××3×5 =34 .
=(3+5)2-4××3×5 =34 .
故四边形似AA
(3)结论:AB2+BC2=AC2或勾股定理的文字叙述.
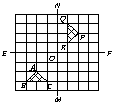 6.如图,8×8方格纸上的两条对称轴EF、MN相交于中心点O,对△ABC分别作下列变换:
6.如图,8×8方格纸上的两条对称轴EF、MN相交于中心点O,对△ABC分别作下列变换:
①先以点A为中心顺时针方向旋转90°,再向右平移4格、向上平移4格;
②先以点O为中心作中心对称图形,再以点A的对应点为中心逆时针方向旋转90°;
③先以直线MN为轴作轴对称图形,再向上平移4格,再以点A的对应点为中心顺时针方向旋转90°.
其中,能将△ABC变换成△PQR的是( D )
(A)①② (B)①③ (C)②③ (D)①②③
 7.请在如图方格纸中,
7.请在如图方格纸中,
画出△ABC绕点A顺时针旋转90°后的图形. 如图

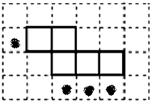 8.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如右图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在右图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(添加所有符合要求的正方形,添加的正方形用阴影表示.)
8.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如右图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在右图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(添加所有符合要求的正方形,添加的正方形用阴影表示.)
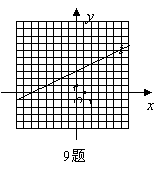
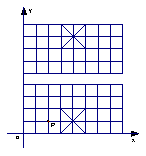 9.如图,我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长均为1),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点P.
9.如图,我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长均为1),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点P.
⑴写出下一步“马”可能到达的点的坐标
;
⑵顺次连接⑴中的所有点,得到的图形是
图形(填“中心对称”、“旋转对称”、“轴对称”);
⑶指出⑴中关于点P成中心对称的点 .
解:(1)(0,0),(0,2),(1,3),(3,3),(4,2),(4,0)
(2)轴对称
(3)(0,0)点和(4,2)点;(0,2)点和(4,0)点
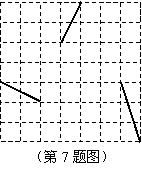 |
10.如图,将网格中的三条线段沿网格线平移后
组成一个首尾相接的三角形,至少需要移动( B )
A.![]() 格 B.
格 B.![]() 格 C.
格 C.![]() 格 D.
格 D.![]() 格
格
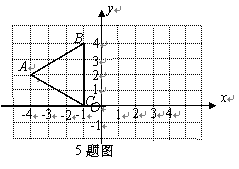
11.已知△ABC 在直角坐标系中的位置如图所示,如果△A'B'C' 与△ABC 关于y轴对称,那么点A的对应点A'的坐标为( D ).
A.(-4,2) B.(-4,-2)
C.(4,-2) D.(4,2)
12.在5×5方格纸中将图①中的图形N平移后的位置如图②所示,那么下面平移中正确的是( C )
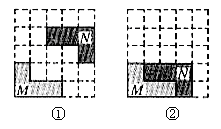
A. 先向下移动1格,再向左移动1格; B. 先向下移动1格,再向左移动2格
C. 先向下移动2格,再向左移动1格; D. 先向下移动2格,再向左移动2格
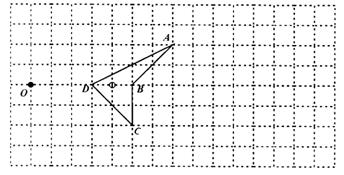
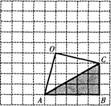
13. 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C。
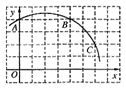 (1)用直尺画出该圆弧所在圆的圆心M的位置;
(1)用直尺画出该圆弧所在圆的圆心M的位置;
(2)若A点的坐标为(0,4),D点的坐标为(7,0),试验证点D是否在经过点A、B、C的抛物线上;
(3)在(2)的条件下,求证直线CD是⊙M的切线。
解:(1)如图1,点M即为所求.
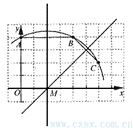
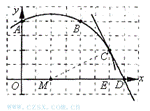
图1 图2
(2)由A(0,4),可得小正方形的边长为1,从而B(4,4)、C(6,2)
设经过点A、B、C的抛物线的解析式为![]()
依题意![]() ,解得
,解得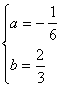
所以经过点A、B、C的抛物线的解析式为![]()
把点D(7,0)的横坐标![]() 代入上述解析式,得
代入上述解析式,得
![]()
所以点D不在经过A、B、C的抛物线上
(3)如图2,设过C点与x轴垂直的直线与x轴的交点为E,连结MC,作直线CD。
所以CE=2,ME=4,ED=1,MD=5
在Rt△CEM中,∠CEM=90°
所以![]()
在Rt△CED中,∠CED=90°
所以![]()
所以![]()
所以∠MCE=90°
因为MC为半径,
 所以直线CD是⊙M的切线
所以直线CD是⊙M的切线
14.如图,直线![]() 是函数
是函数![]() 的图象.若点
的图象.若点![]() 满足
满足![]() ,且
,且![]() ,则
,则![]() 点的坐标可能是( B )
点的坐标可能是( B )
A.(7,5) B.(4,6)
C.(3,4) D.(-2,1)
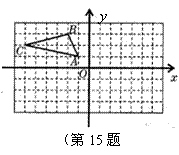
15.如图,在网格中有两个全等的图形(阴影部分),用这两个图形拼成轴对称图形,试分别在图(1)、(2)中画出两种不同的拼法。
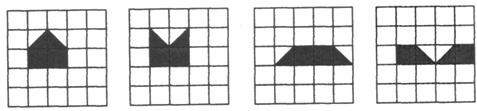
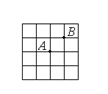
16.已知在正方形网格中,每个小方格都是边长为1的正方形,A、B 两点在小方格的顶点上,位置如图所示,点C也在小方格的顶点上,且以A、B、C为顶点的三角形面积为1,则点C的个数为( )D
(A)3个 (B)4个 (C)5个 (D)6个
 |
17.如图,在平面直角坐标系中,请按
下列要求分别作出![]() 变换后的图形
变换后的图形
(图中每个小正方形的边长为![]() 个单位):
个单位):
(1)向右平移![]() 个单位;(2)关于
个单位;(2)关于![]() 轴对称; (3)绕点
轴对称; (3)绕点![]() 顺时针方向旋转
顺时针方向旋转![]() .
.
∴ x=3
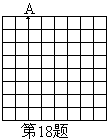
18.已知△ABC的三个顶点坐标如下表:
(1)将下表补充完整,并在直角坐标系中,画出△![]() ;
;
(2)观察△ABC与△![]() ,写出有关这两个三角形关系的一个正确结论。
,写出有关这两个三角形关系的一个正确结论。
| ( | ( |
| A (2,1) |
|
| B (4,3) |
|
| C (5,1) |
|
20.(1)
| ( | ( |
| A (2,1) |
|
| B (4,3) |
|
| C (5,1) |
|
正确答出有关两三角形形状、大小、位置等关系,如△ABC∽△![]() 、周长比、相似比、位似比等
、周长比、相似比、位似比等
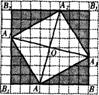
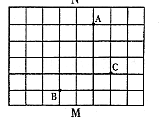 19、以如图所示的方格纸中,每个小正方形的边长为1,如果以MN所在的直线为Y轴,以小正方形的边长为单位长度建立平面直角坐标系,使A点与B点关于原点对称,则这时C点的坐标可能是( )B
19、以如图所示的方格纸中,每个小正方形的边长为1,如果以MN所在的直线为Y轴,以小正方形的边长为单位长度建立平面直角坐标系,使A点与B点关于原点对称,则这时C点的坐标可能是( )B
A、(1,3) B、(2,-1)
 C、2,1)
D、(3,1)
C、2,1)
D、(3,1)
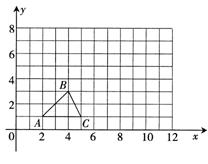
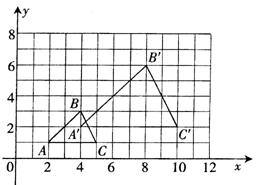
20.、如图:在6×6的网格(小正方形的边长为1)中有一个三角形ABC,则三角形ABC的周长是 (精确到0.001)8.606
21.正方形网格中,小格的顶点叫做格点。小华按下列要求作图:①在正方形网格的三条不同的实线上各取一个格点,使其中任意两点不在同一条实线上;②连结三个格点,使之构成直角三角形。小华在左边的正方形网格中作出了Rt⊿ABC。请你按照同样的要求,在右边的两个正方形网格中各画出一个直角三角形,并使三个网格中的直角三角形互不全等。
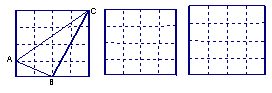
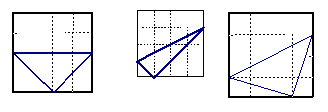
|
 23.如图,(1)若把图中小人平移,使点
23.如图,(1)若把图中小人平移,使点![]() 平移到点
平移到点![]() ,请你在图中画出平移后的小人.
,请你在图中画出平移后的小人.
(2)若图中小人是一名游泳者的位置,他要先游到岸边![]() 上点
上点![]() 处喝水后,再游到
处喝水后,再游到![]() ,但要使游泳的路程最短,试在图中画出点
,但要使游泳的路程最短,试在图中画出点![]() 的位置.
的位置.
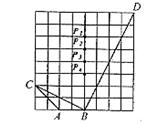
 24.如图5方格中,有两个图形.
24.如图5方格中,有两个图形.
(1)画出图形(1)向右平移7个单位的像![]() ;
;
(2)画出像![]() 关于直线
关于直线![]() 轴反射的像
轴反射的像![]() ;
;
(3)将像![]() 与图形(2)看成一个整体图形,
与图形(2)看成一个整体图形,
请写出这个整体图形的对称轴的条数.
解:(1)图略; (2)图略; (3)2条.
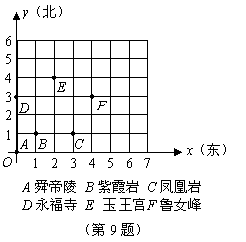 25.如图为九嶷山风景区的几个景点的平面图,以舜帝陵为坐标原点,建立平面直角坐标系,则玉王宫岩所在位置的坐标为 .
25.如图为九嶷山风景区的几个景点的平面图,以舜帝陵为坐标原点,建立平面直角坐标系,则玉王宫岩所在位置的坐标为 .![]()
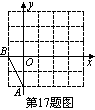
26. 在方格纸中,每个小格的顶点称为格点,以格点连线为边的三角形叫格点三角形.在如图5×5的方格中,作格点△ABC和△OAB相似(相似比不为1),则点C的坐标是____________.(4,0)或(3,2)
27.如图,图中的小方格都是边长为1的正方形, △ABC与△A′ B′ C′是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
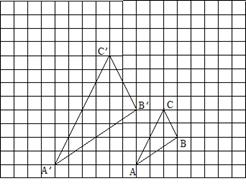 (1)画出位似中心点0;
(1)画出位似中心点0;
(2)求出△ABC与△A′B′C′的位似比;
解:位似比为 1:2
(3)以点0为位似中心,再画一个△A1B
 28. 如图所示,A、B是4×5网络中的格点,网格中的每个小正方形的边长为1,请在图中清晰标出使以A、B、C为顶点的三角形是等腰三角形的所有格点C的位置.
如图,
28. 如图所示,A、B是4×5网络中的格点,网格中的每个小正方形的边长为1,请在图中清晰标出使以A、B、C为顶点的三角形是等腰三角形的所有格点C的位置.
如图,
 29. (2006·江 西 省)请在由边长为1的小正三角形组成的虚线网格中画出一个所有顶点均在格点上,且至少有一条边长为无理数的等腰三角形.
29. (2006·江 西 省)请在由边长为1的小正三角形组成的虚线网格中画出一个所有顶点均在格点上,且至少有一条边长为无理数的等腰三角形.
本题解答不惟一,只要符合题意即可得满分,下面画法供参考: