第二讲 一次函数的图象和性质
知识网络
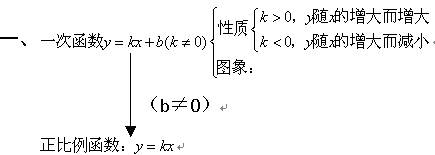
二、选择题
1.已知一次函数
,若
随着
的增大而减小,则该函数图象经过:
(A)第一,二,三象限 (B)第一,二,四象限
(C)第二,三,四象限 (D)第一,三,四象限
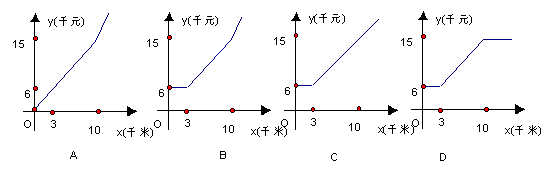
2.某市的出租车的收费标准如下：3千米以内的收费6元；3千米到10千米部分每千米加收1.3元；10千米以上的部分每千米加收1.9元。那么出租车收费y（元）与行驶的路程x(千米)之间的函数关系用图象表示为
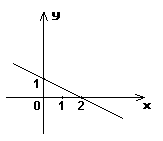
3.阻值为
和
的两个电阻，其两端电压
关于电流强度
的函数图象如图，
则阻值
（A）＞ （B）＜ （C）＝ （D）以上均有可能
 |
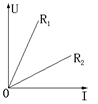4.若函数
(
为常数)的图象如图所示，那么当
时，的取值范围是
A、
B、
C、
D、
5.下列函数中，一次函数是（ ）.
（A）
（B）
（C）
（D）
6.一次函数y=x+1的图象在（ ）.
（A）第一、二、三象限 （B）第一、三、四象限
（C）第一、二、四象限 （D）第二、三、四象限
7.将直线y=2x向上平移两个单位，所得的直线是
A．y=2x+2 B．y=2x-2 C．y=2（x-2） D．y=2（x+2）
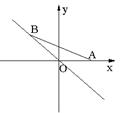
8.如图，已知点A的坐标为(1，0)，点B在直线
上运动，当线段AB最短时，点B的坐标为
A. (0，0) B. 
C. 
D. 
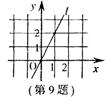
9．如图，把直线ｌ沿x轴正方向向右平移2个单位得到直线ｌ′，则直线l/的解析式为
A.y=2x+4 B.y=-2x+2 C.y=2x-4 D.y=-2x-2
10.直线y=kx+1一定经过点( )
A．(1，0) B．(1，k) C．(0，k) D．(0，1)
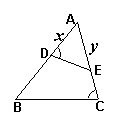11.如图，在△ABC中，点D在AB上，点E在AC上，若∠ADE=∠C，
且AB=5，AC=4，AD=x，AE=y，则y与x的关系式是( )
A．y=5x B．y=
x C．y=
x D．y=
x
12.下列函数中，是正比例函数的为
A.y＝
B.y＝
C.y＝5x－3 D.y＝6x2－2x－1
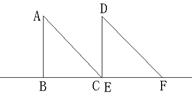
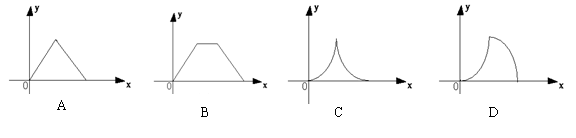
13如图，△ABC和△DEF是两个形状大小完全相同的等腰直角三角形，∠B=∠DEF=90°，点B、C、E、F在同一直线上．现从点C、E重合的位置出发，让△ABC在直线EF上向右作匀速运动，而△DEF的位置不动．设两个三角形重合部分的面积为，运动的距离为．下面表示与的函数关系式的图象大致是（ ）
 |
三、填空题
1.若正比例函数y=mx (m≠0)和反比例函数y=
(n≠0)的图象都经过点(2,3)，则m=______，n=_________ .
2.如果函数
，那么
3.点A(2，4)在正比例函数的图象上，这个正比例函数的解析式是
4.若函数的图象经过点（1，2），则函数的表达式可能是 （写出一个即可）．
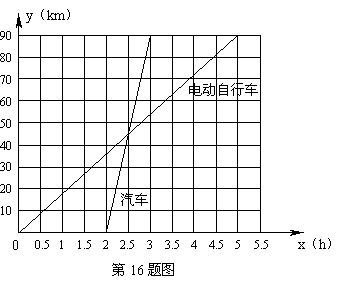
5.如图，表示甲骑电动自行车和乙驾驶汽车均行驶90km的过程中，行使的路程与经过的时间之间的函数关系．请根据图象填空：
出发的早，早了 小时， 先到达，先
到 小时，电动自行车的速度为 km / h，汽车的速度为 km / h．
6.某电信公司推出手机两种收费方式：A种方式是月租20元，B种方式是月租0元．一个月的本地网内打出电话时间t(分钟)与打出电话费s(元)的函数关系如图3，当打出电话150分钟时，这两种方式电话费相差 元．
7.若一次函数y=ax+1―a中，y随x的增大而增大，且它的图像与y轴交于正半轴，则a―1+
=
。
8.已知，如图，一轮船在离A港10千米的P地出发，向B港匀速行驶，30分钟后离A港26千米(未到达B港)，设出发x小时后，轮船离A港y千米(未到达B港)，则 y 与x的函数关系式为
四、解答题
1.某产品每件成本10元，试销阶段每件产品的日销售价（元）与产品的日销售量（件）之间的关系如下表：
|
| 15 | 20 | 25 | 30 | … |
|
| 25 | 20 | 15 | 10 | … |
⑴ 在草稿纸上描点，观察点的颁布，建立与的恰当函数模型。
⑵ 要使每日的销售利润最大，每件产品的销售价应定为多少元？此时每日销售利润是多少元？
2.】李红和张明正在玩掷骰子游戏，两人各掷一枚骰子。
⑴ 当两枚骰子点数之积为奇数时，李红得3分，否则，张明得1分，这个游戏公平吗？为什么？
⑵ 当两枚骰子的点数之和大于7时，李红得1分，否则张明得1分，这个游戏公平吗？为什么？如果不公平，请你提出一个对双方公平的意见。
3.小明子在银行存入一笔零花钱，已知这种储蓄的年利率为n
。若设到期后的本息和（本金+利息）为y(元)，存入的时间为x（年），那么
（1）下列那个图像更能反映y与x之间的函数关系？从图中你能看出存入的本金是多少元？一年后的本息和是多少元？
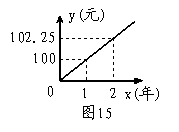
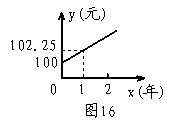
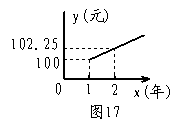
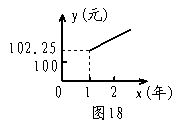
（2）根据（1）的图象，求出y于x的函数关系式（不要求写出自变量x的取值范围），并求出两年后的本息和。
4.某商场的营业员小李销售某种商品，他的月收入与他该月的销售量成一次函数关系，其图象如图所示，根据图象提供的信息，解答下列问题：
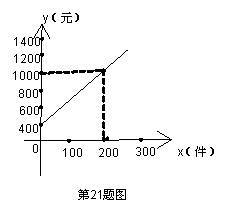
（1）求出小李的个人月收入y（元）与他的月销售量x（件）（
之间的函数关系式；
（2）已知小李4月份的销售量为250件，求小李4月份的收入是多少元？
5、如图，在平面直角坐标系中，正方形AOCB的边长为6，O为坐标原点，边
OC在x轴的正半轴上，边OA在y轴的正半轴上，E是边AB上的一点，直线EC交y轴于F，且S△FAE∶S四边形AOCE＝1∶3。
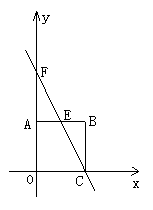
⑴ 求出点E的坐标； ⑵ 求直线EC的函数解析式.
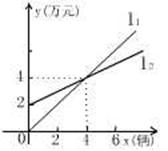6如图，
表示神风摩托车厂一天的销售收入与摩托车销售量的关系；
表示摩托车厂一天的销售成本与销售量的关系。
(1)写出销售收入与销售量之间的函数关系式；
(2)写出销售成本与销售量之间的函数关系式；
(3)当一天的销售量为多少辆时，销售收入等于销售成本；
(4)当一天的销售超过多少辆时，工厂才能获利？（利润=收入-成本）
7.在“五一黄金周”期间，小明和他的父母坐游船从甲地到乙地观光，在售票大厅看到表（一）， 爸爸对小明说：“我来考考你，你能知道里程与票价之间有何关系吗？”小明点了点头说：“里程与票价是一次函数关系，具体是……”．
在游船上，他注意到表（二），思考一下，对爸爸说：“若游船在静水中的速度不变，那么我还能算出它的速度和水流速度．”爸爸说：“你真聪明！”亲爱的同学，你知道小明是如何求出的吗？请你和小明一起求出：
（1）票价（元）与里程（千米）的函数关系式；
（2）游船在静水中的速度和水流速度．
| 里程（千米） | 票价（元） | |
| 甲→乙 | 16 | 38 |
| 甲→丙 | 20 | 46 |
| 甲→丁 | 10 | 26 |
| … | … | … |
| 出发时间 | 到达时间 | |
| 甲→乙 | 8:00 | 9:00 |
| 乙→甲 | 9:20 | 10:00 |
| 甲→乙 | 10:20 | 11:20 |
| … | … | … |
表（一） 表（二）
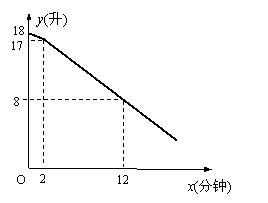
8. 
教室里放有一台饮水机（如图），饮水机上有两个放水管．课间同学们依次到饮水机前用茶杯接水．假设接水过程中水不发生泼洒，每个同学所接的水量都是相等的．两个放水管同时打开时，他们的流量相同.放水时先打开一个水管，过一会儿，再打开第二个水管，放水过程中阀门一直开着．饮水机的存水量y（升）与放水时间x（分钟）的函数关系如图所示：
（1）求出饮水机的存水量y（升）与放水时间x（分钟）(x≥2)的函数关系式；
（2）如果打开第一个水管后，2分钟时恰好有4个同学接水结束，则前22个同学接水结束共需要几分钟？
（3）按（2）的放法，求出在课间10分钟内班级中最多有多少个同学能及时接完水？
 |
9.某出版社出版一种适合中学生阅读的科普读物，若该读物首次出版印刷的印数不少于5000册时，投入的成本与印数间的相应数据如下：
| 印数x（册） | 5000 | 8000 | 10000 | 15000 | …… |
| 成本y（元） | 28500 | 36000 | 41000 | 53500 | …… |
（1）经过对上表中数据的探究，发现这种读物的投入成本y（元）是印数x（册）的一次函数，求这个一次函数的解析式（不要求写出x的取值范围）；
（2）如果出版社投入成本48000元，那么能印该读物多少册？
10.阅读：我们知道，在数轴上，x＝1表示一个点，而在平面直角坐标系中，x＝1表示一条直线；我们还知道，以二元一次方程2x－y＋1＝0的所有解为坐标的点组成的图形就是一次函数y＝2x＋1的图象，它也是一条直线，如图①.
观察图①可以得出：直线＝1与直线y＝2x＋1的交点P的坐标（1，3）就是方程组
的解，所以这个方程组的解为
在直角坐标系中，x≤1表示一个平面区域，即直线x＝1以及它左侧的部分，如图②；y≤2x＋1也表示一个平面区域，即直线y＝2x＋1以及它下方的部分，如图③。
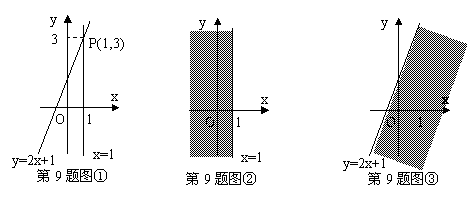
回答下列问题：
（1）在直角坐标系中，用作图象的方法求出方程组
的解；
（2）用阴影表示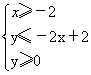
，
所围成的区域。
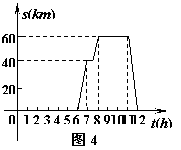
11一天上行6点钟，汪老师从学校出发，乘车上市里开会，8点准时到会场，中午12点钟回到学校，他这一段时间内的行程S（km）（即离开学校的距离）与时间（h）的关系可用图4中的折线表示，根据图4提供的有关信息，解答下列问题：
（1）开会地点离学校多远？
（2）求出汪老师在返校途中路程S（km）与时间t（h）的函数关系式；
（3）请你用一段简短的话，对汪老师从上午6点到中午12点的活动情况进行描述．
12.已知正比例函数y=kx与反比例函数y=
的图象都过A（m,，1）点，求此正比例函数解析式及另一个交点的坐标．
13.小明暑假到华东第一高峰—黄岗山（位于武夷山境内）旅游，导游提醒
大家上山要多带一件衣服，并介绍当地山区气温会随海拔高度的增加而下降.沿途小明利用随身带的登山表（具有测定当前位置高度和气温等功能）测得以下数据：
| 海拔高度x米 | 400 | 500 | 600 | 700 | … |
| 气温y(0C） | 28.6 | 28.0 | 27.4 | 26.8 | … |
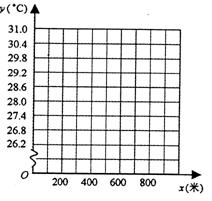
（1）以海拔高度为x轴，气温为y轴，根据上表提供的数据在下列直角坐标系中描点；
（2）观察（1）中所苗点的位置关系，猜想y与x之间的函数关系，求出所猜想的函数表达式，并根据表中提供的数据验证你的猜想；
（3）如果小明到达山顶时，只告诉你山顶的气温为18.1，你能计算出黄岗山的海拔高度大约是多少米吗？
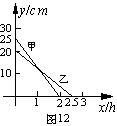
13.在一次蜡烛燃烧实验中，甲、乙两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)的关系如图12所示。请根据图象所提供的信息解答下列问题：
⑴甲、乙两根蜡烛燃烧前的高度分别是 ，从点燃到燃尽所用的时间分别是 ；
⑵分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式；
⑶当x为何值时，甲、乙两根蜡烛在燃烧过程中的高度相等？
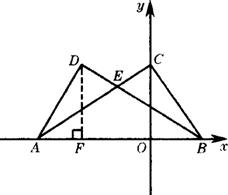
14. 
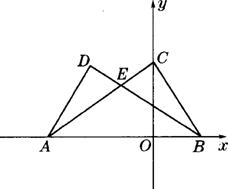如图，A、B两点的坐标分别是(x1，0)、(x2，O)，其中x1、x2是关于x的方程x2+2x+m-3=O的两根，且x1<0<x2．
(1)求m的取值范围；
(2)设点C在y轴的正半轴上，∠ACB=90°，∠CAB=30°，求m的值；
(3)在上述条件下，若点D在第二象限，△DAB≌△CBA，求出直线AD的函数解析式：
参考答案
一、选择题
1.B 2.B 3.A 4.D 5. B 6.A 7.A 8.B
9.C 10.D 11.C 12. A 13.C
二、填空题
1. 
6. 2.
3.
4.答案不唯一；如
5.甲（或电动自行车） 2 乙（或汽车） 2 18 90
6.10 7. 1 8.
三、解答题
1、⑴ 经观察发现各点分布在一条直线上 ∴设 （k≠0）
用待定系数法求得
⑵ 设日销售利润为z 则
=
当x=25时，z最大为225
每件产品的销售价定为25元时，日销售利润最大为225元
2、⑴ 这个游戏对双方公平 ∵P(奇)=
， P(偶)=
3 P(奇)= P(偶)， ∴这个游戏对双方公平
⑵ 不公平
列表：
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
得：P(和大于7)=
，P(和小于或等于7)=
李红和张明得分的概率不等，∴这个游戏对双方不公平
3、（1）图16能反映y与x之间的函数关系
从图中可以看出存入的本金是100元
一年后的本息和是102.25元
（2）设y与x的关系式为：y=100 nx+100
把（1，102.25）代入上式，得n=2.25
∴y=2.25x+100
当x=2时，
y=2.25*2+100=104.5(元)
4、（1）由题意可设与的函数关系式为：
由图象可知：当
时，
，
时，
有
解得，
与的函数关系式为：
（2）当
时，
（元）
5、⑴ ∵S△FAE∶S四边形AOCE＝1∶3， ∴S△FAE∶S△FOC＝1∶4，
∵四边形AOCB是正方形， ∴AB∥OC， ∴△FAE∽△FOC，
∴AE∶OC＝1∶2，
∵OA＝OC＝6， ∴AE＝3， ∴点E的坐标是(3,6)
⑵ 设直线EC的解析式是y＝kx＋b，
∵直线y＝kx＋b过E(3,6)和C(6，0)
∴，解得：
∴直线EC的解析式是y＝－2x＋12
6、1）y=x
（2）设
∵直线过（0，2）、（4，4）两点
∴
又
∴
∴
（3）由图像知，当
时，销售收入等于销售成本
或
∴
（4）由图像知：当
时，工厂才能获利
或
时，即时，才能获利。
7、（1）设票价与里程关系为，
当＝10时，＝26；当＝20时，＝46；
∴
解得：
．
∴票价与里程关系是
．
（2）设游船在静水中速度为
千米/小时，水流速度为
千米/小时，
根据图中提供信息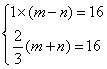，得
， 解得：
8、设存水量y与放水时间x的解析式为y=kx＋b
把（2，17）、（12，8）代入y=kx＋b得
解得k=－
，b=
y=－x＋ （2≤x≤
）
（2）由图可得每个同学接水量是0.25升 则前22个同学需接水0.25×22=5.5升
存水量y=18－5.5=12.5升 ∴12.5=－x＋ ∴x=7
∴前22个同学接水共需7分钟．
（3）当x=10时 存水量y=－×10＋=
用去水18－=8.2升 8.2÷0.25=32.8
∴课间10分钟最多有32人及时接完水．
或 设课间10分钟最多有z人及时接完水
由题意可得 0.25z≤8.2 z≤32.8
9、（1）设所求一次函数的解析式为y＝kx＋b，
则
解得k＝
，b＝16000。
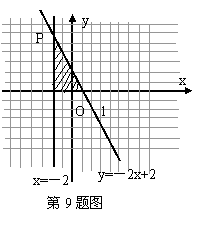∴所求的函数关系式为y＝x＋16000。
（2）∵48000＝x＋16000。 ∴x＝12800。
10、1）如图所示，
在坐标系中分别作出直线x＝－2和直线y＝－2x＋2，
这两条直线的交点是P（－2，6）。
则
是方程组的解。
（2）如阴影所示。
11、1）开会地点离学校有60千米
（2）设汪老师在返校途中S与t的函数关系式为S＝kt＋b（k≠0）．
由图可知，图象经过点（11,60）和点（12,0）
∴
解之，得
∴S＝－60t＋720（11≤t≤12）
（3）汪老师由上午6点钟从学校出发，乘车到市里开会，到了40公里处时，发生了堵车，堵了约30分钟才通车，在8占钟准里到达会场开了3个小时的会，会议一结束就返校，结果在12点钟到校．
12、∵y=图象过A（m，1）点，则1=
，∴m=3，即A（3，1）．将A（3，1）代入
y=kx，得k=
，∴正比例函数解析式为y=x．又x=∴x=±3．当x=3时，y=1；当x=－3时，y=－1．∴另一交点为（－3，－1）．
13、（1） 四个点都描对得2分
（2）猜想：Y与X之间的函数关系式可能是一次函数（若学生未先写猜想，而在后继解答中完成了对一次函数的就假设，仍可得这1分）
求解：设函数表达式为：y = k x + b ，把 （400，28.6） ， （500，28.0）代入y = k x + b，得：
解得：k = - 0.006 ,
b = 31
∴y与x之间的函数关系式可能是y = -0.006x + 31
当x = 700时 ,y = - 0.006×700 +31 = 26.8
∴ 点 （600，27.4）， （700，26.8）都在函数y = -0.006x + 31的图象上
∴y与x之间的函数关系式是y = -0.006x + 31
（3），当Y=18.1时，有 –0.006x +31 = 18.1
解得 x = 2150 (米)
∴ 黄岗山的海拔高度大约是 2150 米
14、⑴30cm，25cm；2h，2.5h；
⑵设甲蜡烛燃烧时y与x之间的函数关系式为
，
由图可知，函数的图象过点（2，0），（0，30），
∴
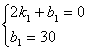解得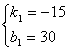
∴
设乙蜡烛燃烧时y与x之间的函数关系式为
，
由图可知，函数的图象过点（2.5，0），（0，25），
∴
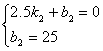解得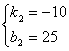
∴
⑶由题意得
，解得 
∴ 当甲、乙两根蜡烛燃烧1h的时候高度相等。
观察图象可知：当0≤x＜1时，甲蜡烛比乙蜡烛高；当1＜x＜2.5时，甲蜡烛比乙蜡烛低。
15、(1)由题意，得
22-4(m-3)=16-m>0①
x1x2=m-3<O． ②
①得m<4．
解②得m<3．
所以m的取值范围是m<3．
(2)由题意可求得∠OCB=∠CAB=30°.
所以BC=2BO，AB=2BC=4BO．
所以A0=3BO(4分)
从而得 x1=-3x2． ③
又因为 x1+x2=-2． ④
联合③、④解得x1=-3，x2=1．
代入x1·x2=m-3，得m=O．
(3)过D作DF⊥轴于F．
从(2)可得到A、B两点坐标为A(-3，O)、B(1，O)．
所以BC=2，AB=4，OC=
因为△DAB≌△CBA，
所以DF=CO=，AF=B0=1，OF=A0-AF=2．
所以点D的坐标为(-2，)．
直线AD的函数解析式为y=x=3