秘密★启用前
初中毕业生学业考试数学试题
数 学
本试卷分选择题和非选择题两部分，共三大题25小题，共4页，满分150分．考试时间120分钟．
注意事项：
1．答卷前，考生务必在答题卡第1面、第3面、第5面上用黑色字迹的钢笔或签字笔填写
自己的考生号、姓名；填写考场试室号、座位号，再用2B铅笔把对应这两个号码的标
号涂黑．
2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题同的答案标号涂黑；如需改动，
用橡皮擦干净后，再选涂其他答案标号；不能答在试卷上．
3．非选择题必须用黑色字迹的钢笔或签字笔作答，涉及作图的题目，用2B铅笔画图．答
案必须写在答题卡各题f=1指定区域内的相应位置上；如需改动，先划掉原来的答案，然
后再写上新的答案；改动的答案也不能超出指定的区域．不准使用铅笔、圆珠笔和涂改
液．不按以上要求作答的答案无效．
4．考生必须保持答题卡的整洁，考试结束后，将本试卷和答题卡一并交回．
第一部分选择题(共30分)
一、选择题(本大题共10小题，每小题3分，共30分． 在每小题给出的四个选项中，只有一项是符合题目要求的．)
1．某市某日的气温是一2℃～6℃，则该日的温差是( )．
(A)8℃ (B)6℃ (C)4℃ (D)一2℃
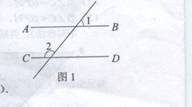
2．如图1，AB／／CD，若∠2=135°，则么∠l的度数是( )．
(A)30° (B)45° (C)60° (D)75°
3．若代数式÷在实数范围内有意义，则X的取值范围为( )．
(A)x>0 (B)x≥0 (C)X≠0 (D)x≥0且X≠1
 |
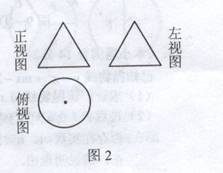4．图2是一个物体的三视图，则该物体的形状是（ ）
(A)圆锥 (B)圆柱
(C)三棱锥 (D)三棱柱
5．一元二次方程
的两个根分别为( )．
(A)Xl=1， x2=3 (B)Xl=1， x2=-3
(C)X1=-1，X2=3 (D)XI=-1， X2=-3
数学试卷第1页(共4页)
6．抛物线Y=X2-1的顶点坐标是( )．
(A)(0，1) (B)(0，一1) (C)(1，0) (D)(一1，0)
7．已知四组线段的长分别如下，以各组线段为边，能组成三角形的是( )．
(A)l，2，3 (B)2，5，8 (C)3，4，5 (D)4，5，10
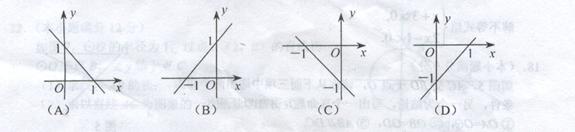
8．下列图象中，表示直线y=x-1的是( )．
 |
9．一个圆柱的侧面展开图是相邻边长分别为10和16的矩形，则该圆柱的底面圆半径是( )．
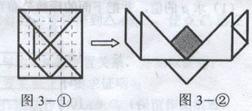
10．如图3一①，将一块正方形木板用虚线划分成36个全等的小正方形，然后，按其中的
实线切成七块形状不完全相同的小木片，制成一副七巧板．用这副七巧板拼成图3一②
的图案，则图3一②中阴影部分的面积是整个图案面积的( )．
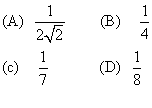
第二部分 非选择题(共120分)
二、填空题(本大题共6小题，每小题3分，共18分．)
11．计算：
÷
=
．
12．计算：
．
13．若反比例函数
的图象经过点(1，一1)，则k的值是
．
14．已知A=
， B=
(n为正整数)．当n≤5时，有A<B；请用计算器计算当
n≥6时，A、B的若干个值，并由此归纳出当以n≥6时，A、B问的大小关系为 ·
15．在某时刻的阳光照耀下，身高160cm的阿美的影长为80cm，她身旁的旗杆影长10m，
则旗杆高为 m．
学试卷第2页(共4页)
16．如图4，从一块直径为a+b的圆形纸板上挖去直径分别为a和b的
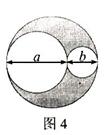两个圆，则剩下的纸板面积为
三、解答题(本大题共9小题，共102 分．解答应写出文字说明、
证明过程或演算步骤)
17．(本小题满分9分) 解不等式组 
 |
19．(本小题满分lO分)
广州市某中学高一(6)班共54名学生，经调查其中40名学生患有不同程度的近视眼
病，初患近视眼病的各个年龄段频数分布如下：
| 初患近视眼病年龄 | 2岁～5岁 | 5岁～8岁 | 8岁～11岁 | 11岁～14岁 | 14岁～17岁 |
| 频数(人数) | 3 | 4 | 13 | a | 6 |
(注：表中2岁～5岁的意义为大于等于2岁并且小于5岁，其它类似)
(1)求a的值，并把下面的频数分布直方图补充画完整；
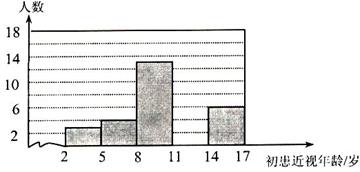
(2)从上研的直方图中你能得出什么结论(只限写出一个结论)?你认为此结论反映了教育与社会的什么问题?
20．(本小题满分10分)
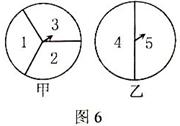如图6，甲转盘被分成3个面积相等的扇形、乙转盘被分
成2个面积相等的扇形．小夏和小秋利用它们来做决定获胜
与否的游戏．规定小夏转甲盘一次、小秋转乙盘一次为一次
游戏(当指针指在边界线上时视为无效，重转)．
(1)小夏说：“如果两个指针所指区域内的数之和为6或7，
则我获胜；否则你获胜”．按小夏设计的规则，请你写出两人获胜的可能性肚分别是多少?
(2)请你对小夏和小秋玩的这种游戏设计一种公平的游戏规则，并用一种合适的方法
(例如：树状图，列表)说明其公平性．
数学试卷第3页(共4页)
21．(本小题满分12分)
目前广州市小学和初中在任校生共有约128万人，其中小学生在校人数比初中生在校人
数的2倍多14万人(数据来源：2005学年度广州市教育统计手册)．
(1)求目前广州市在校的小学生人数和初中生人数；
(2)假设今年小学生每人需交杂费500元，初中生每人需交杂费1000元，而这些费
用全部由广州市政府拨款解决，则广州市政府要为此拨款多少?
 |
22．(本小题满分12分)
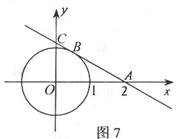
如图7
⊙0的半径为1，过点A(2，0)的直线切
⊙0于点B，交y轴于点C.
(1)求线段AB的长；
(2)求以直线AC为图象的一次函数的解析式．
23．(本小题满分12分)
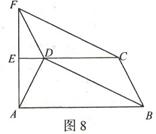图8是某区部分街道示意图，其中CE垂直平分AF，
AB／／DC，BC／／DF．从B站乘车到E站只有两条路线有直
接到达的公交车，路线1是B---D---A---E，路线2是
B---C---F---E，请比较两条路线路程的长短，并给出证明．
24．(本小题满分14分)
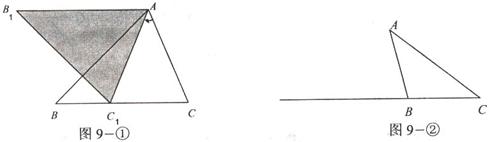
在
ABC中，AB=BC，将ABC绕点A沿顺时针方向旋转得A1B1C1，使点Cl落在
直线BC上(点Cl与点C不重合)，
(1)如图9一①，当
C>60°时，写出边ABl与边CB的位置关系，并加以证明；
(2)当C=60°时，写出边ABl与边CB的位置关系(不要求证明)；
(3)当C<60°时，请你在图9一②中用尺规作图法作出△AB1C1(保留作图痕迹，
不写作法)，再猜想你在(1)、(2)中得出的结论是否还成立?并说明理由．
 |
25．(本小题满分14分)
已知抛物线Y=x2+mx一2m2(m≠0)．
(1)求证：该抛物线与X轴有两个不同的交点；
(2)过点P(0，n)作Y轴的垂线交该抛物线于点A和点B(点A在点P的左边)，是
否存在实数m、n，使得AP=2PB?若存在，则求出m、n满足的条件；若不存在，
请说明理由．
数学试卷第4页(共4页)