初中毕业生数学学业模拟考试(一)
数 学 试 题
本试卷分选择题和非选择题两部分,共三大题25小题,共4页,满分150分.考试时间120分钟.可使用计算器.
注意事项:
1. 答卷前,考生务必在答卷密封线内用黑色字迹的钢笔或签字笔填写自己的考生号、姓名。
2. 选择题答案用2B铅笔填涂在学校发的答题卡上,其余试题必须用黑色字迹的钢笔或签字笔作答,涉及作图的题目,用2B铅笔画图。答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;改动的答案也不能超出指定的区域。不准使用铅笔(除作图外)、圆珠笔和涂改液。不按以上要求作答的答案无效。
第一部分 选择题 (共30分)
一、选择题(本大题共10小题,每小题3分,满分30分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 生物学家发现一种病毒的长度约为0.000043mm,这个数用科学记数法表示为( * ).
(A)4.3×10-4 mm (B)4.3×10-5 mm (C)4.3×10-6 mm (D)43×10-5 mm
2. 下列图形中,不是正方体平面展开图的是( * ).
 |
(A) (B) (C) (D)
3. 设—元二次方程![]() 的两个实根为
的两个实根为![]() 和
和![]() ,则下列结论正确的是( * ).
,则下列结论正确的是( * ).
(A) ![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
4. 二次函数y=x2的图象向上平移3个单位,得到新的图象的二次函数表达式是( * ).
 (A)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5. 在函数![]() 中,自变量
中,自变量![]() 的取值范围是( * ).
的取值范围是( * ).
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
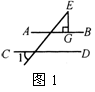
6. 如图1,AB∥CD,EG⊥AB,垂足为G.若∠1=50°,则∠E=( * ).
(A)60° (B)50° (C)40° (D)30°
7. 要做甲、乙两个形状相同(相似)的三角形框架,已知甲三角形框架三边的长分别为50 cm、60 cm、80 cm,乙三角形框架的一边长为20 cm,则符合条件的乙三角形框架共有( * ).
(A)1种 (B)2种 (C)3种 (D)4种
8. 下列计算正确的是( * ).
(A)(-2)0=-1 (B)-23=-8 (C)-2-(-3)=-5 (D)3-2=-6
9. 直线![]() 与
与![]() 轴交于点(-4
, 0),且
轴交于点(-4
, 0),且![]() ,则当
,则当![]() > 0时,
> 0时,![]() 的取值范围是( * ).
的取值范围是( * ).
(A)![]() <0 (B)
<0 (B)![]() >0 (C)
>0 (C)![]() <-4 (D)
<-4 (D)![]() >-4
>-4

10. 已知:如图2,![]() 是
是![]() 的角平分线,且
的角平分线,且 ![]() ,则
,则![]() 与
与![]() 的面积之比为( * ).
的面积之比为( * ).
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
第二部分 非选择题(共120分)
 二、填空题:(本大题共6小题,每小题3分,共18分)
二、填空题:(本大题共6小题,每小题3分,共18分)
11. 不等式组![]() 的解集是 * .
的解集是 * .
12. 二元一次方程![]() 的一个整数解可以是 * .
的一个整数解可以是 * .
13. ⊙O的半径为5cm,圆心到弦AB的距离为3cm,则弦AB的长为 * cm.
14. 已知![]() ,
,![]() (
(![]() ),请用计算器计算当
),请用计算器计算当![]() 时,
时,![]() 、
、![]() 的若干个值,并由此归纳出当
的若干个值,并由此归纳出当![]() 时,
时,![]() 、
、![]() 间的大小关系为 * .
间的大小关系为 * .
15. 小明要制作一个圆锥模型,其侧面是由一个半径为9cm,圆心角为240°的扇形纸板制成的,还需要一块圆形纸板做底面,那么这块圆形纸板的直径为 * cm.
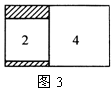
16. 如图3,矩形内有两个相邻的正方形,面积分别为4和2,那么阴影部分的面积为 * .
三、解答题:(本大题共9小题,共102分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分9分)解方程:![]()
18.(本小题满分9分)
小王家里装修,他去商店买灯,商店柜台里现有功率为100瓦的白炽灯和40瓦的节能灯,它们的单价分别为2元和32元,经了解知这两种灯的照明效果和使用寿命都一样. 已知小王家所在地的电价为每度0.5元,请问当这两种灯的使用寿命超过多长时间时,小王选择节能灯才合算. [用电量(度)=功率(千瓦)×时间(时)]
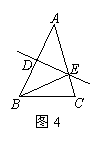 19. (本小题满分10分)
19. (本小题满分10分)
如图4,在△ABC中,BC = 8 cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18 cm,求AC的长.
20.(本小题满分10分)
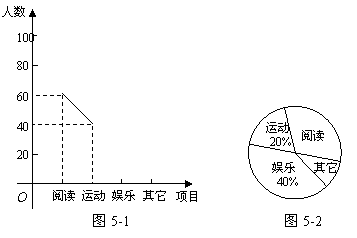
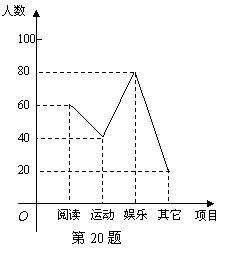
某中学团委会为研究该校学生的课余活动情况,采取抽样的方法,从阅读、运动、娱乐、其它等四个方面调查了若干名学生的兴趣爱好,并将调查的结果绘制了如下的两幅不完整的统计图(如图5-1,图5-2),请你根据图中提供的信息解答下列问题:
(1)在这次研究中,一共调查了多少名学生?
(2)“其它”在扇形图中所占的圆心角是多少度?
(3)补全频数分布折线图.
 |
21. (本小题满分12分)
杨华与季红用5张同样规格的硬纸片做拼图游戏,正面如图6-1所示,背面完全一样,将它们背面朝上搅匀后,同时抽出两张.规则如下:当两张硬纸片上的图形可拼成电灯或小人时,杨华得1分;当两张硬纸片上的图形可拼成房子或小山时,季红得1分(如图6-2).问题:游戏规则对双方公平吗?请说明理由;若你认为不公平,如何修改游戏规则才能使游戏对双方公平?

22. (本小题满分12分)
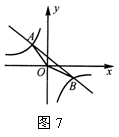
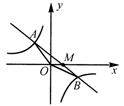
如图7,已知一次函数y=kx+b的图象与反比例函数![]() 的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是-2.
的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是-2.
求:(1)一次函数的解析式; (2)△AOB的面积.
23. (本小题满分12分)
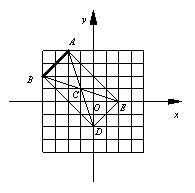
如图8是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
 (1)请在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);
(1)请在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);
(2)在第二象限内的格点(网格线的交点)上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,求C点坐标和△ABC的周长(结果保留根号);
(3)画出△ABC以点C为旋转中心,旋转180°后的△DEC,连结AE和BD,试说明四边形ABDE是什么特殊四边形,并说明理由.
24. (本小题满分14分)
 如图9,以A(0,
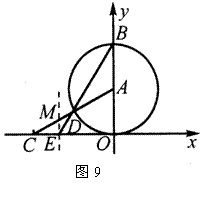
如图9,以A(0,![]() )为圆心的圆与x轴相切于坐标原点O,与y轴相交于点B,弦BD的延长线交x轴的负半轴于点E,且∠BEO=60°,AD的延长线交x轴于点C.
)为圆心的圆与x轴相切于坐标原点O,与y轴相交于点B,弦BD的延长线交x轴的负半轴于点E,且∠BEO=60°,AD的延长线交x轴于点C.
(1)分别求点E、C的坐标;
(2)求经过A、C两点,且以过E而平行于y轴的直线为对称轴的抛物线的函数解析式;
(3)设抛物线的对称轴与AC的交点为M,试判断以M点为圆心,ME为半径的圆与⊙A的位置关系,并说明理由.
25. (本小题满分14分)
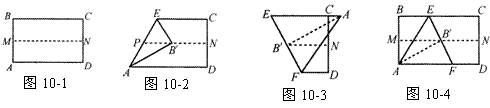
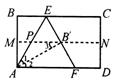
取一张矩形纸片进行折叠,具体操作过程如下:第一步:先把矩形ABCD对折,折痕为MN,如图10-1;第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为B',得Rt△AB'E,如图10-2;第三步:沿EB'线折叠得折痕EF,使A点落在EC的延长线上,如图10-3.
利用展开图10-4探究:
(1)△AEF是什么三角形?证明你的结论;
(2)对于任一矩形,按照上述方法是否都能折出这种三角形?请说明理由.
 |
初中毕业生数学学业模拟考试
数学参考答案
一、选择题:(每小题3分,共30分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | D | D | B | A | C | C | B | D | A |
二、填空题:(每小题3分,共18分)
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 |
| 答案 |
|
| 8 |
| 12 |
|
三、解答题:(本大题共9小题,共102分.)
注:下面只是给出各题的一般解法,其余解法对应给相应的分数
17、(9分)
解:![]() …………………………(1分)
…………………………(1分)
![]() ……………………………(3分)
……………………………(3分)
![]() ……………………………(5分)
……………………………(5分)
![]() ……………………………(7分)
……………………………(7分)
经检验:![]() 是原方程的根 ……………………………(9分)
是原方程的根 ……………………………(9分)
18、(9分)
解:设这两种灯的使用寿命为![]() 小时,则
…………………………(1分)
小时,则
…………………………(1分)
![]() …………………………(6分)
…………………………(6分)
解得
![]() …………………………(8分)
…………………………(8分)
答:这两种灯的使用寿命超过1000小时时,小王选择节能灯才合算.
…………………………(9分)
19、(10分)
解:∵△BCE的周长等于18 cm,BC = 8 cm
∴![]() ……………………………(4分)
……………………………(4分)
∵DE垂直平分AB
∴AE=BE ……………………………(8分)
∴![]() , 即
, 即![]() ………………………(10分)
………………………(10分)
 20、(10分)
20、(10分)
解:(1)200名 …………………………(3分)
(2)![]() ……………………………(6分)
……………………………(6分)
(3)如图 ……………………………(10分)
21、(12分)
解:(1)这个游戏对双方不公平.……(2分)
∵![]() ;
;![]() ;
;
![]() ;
;![]() ,
,
∴杨华平均每次得分为![]() (分);
(分);
季红平均每次得分为![]() (分). ………………(8分)
(分). ………………(8分)
∵![]() <
<![]() ,∴游戏对双方不公平.
………………(9分)
,∴游戏对双方不公平.
………………(9分)
(2)改为:当拼成的图形是小人时杨华得3分,其余规则不变,
就能使游戏对双方公平.(答案不惟一,其他规则可参照给分) …(12分)
22、(12分)
解:(1)把![]() 代入
代入![]() 中,得
中,得![]() .∴ 点A(-2,4).…(1分)
.∴ 点A(-2,4).…(1分)
把![]() 代入
代入![]() 中,得
中,得![]() .∴点B(4,-2). ………(2分)
.∴点B(4,-2). ………(2分)
把A、B两点的坐标代入y=kx+b中,得
![]() 解得
解得![]() …………………………(6分)
…………………………(6分)
∴ 所求一次函数的解析式为y=-x+2.…………………………(7分)
 (2)当y=0时,x=2.∴ y=-x+2与x轴交于点M(2,0),
(2)当y=0时,x=2.∴ y=-x+2与x轴交于点M(2,0),
即![]() .…………………………(9分)
.…………………………(9分)
∴![]()
![]()
![]() =6. …………………(12分)
=6. …………………(12分)
 23、(12分)
23、(12分)
解:(1)坐标系如图;…………………………(2分)
(2)![]() …………………………(4分)
…………………………(4分)
![]() …………………(6分)
…………………(6分)
(3)画图正确; …………………………(8分)
矩形; …………………………(10分)
理由:由题目和旋转性质可知![]() ……………………(12分)
……………………(12分)
24、(14分)
解:(1)在Rt△EOB中,![]() ,
,
∴ 点E的坐标为(-2,0).…………………………(2分)
在Rt△COA中,![]() ,
,
∴ 点C的坐标为(-3,0).…………………………(4分)
(2)∵ 点C关于对称轴![]() 对称的点的坐标为F(-1,0),
对称的点的坐标为F(-1,0),
点C与点F(-1,0)都在抛物线上.…………………………(6分)
设![]() ,用
,用![]() 代入得
代入得
![]() ,∴
,∴ ![]() . ∴
. ∴ ![]() ,即
,即
![]() .
…………………………(9分)
.
…………………………(9分)
(3)⊙M与⊙A外切,证明如下:…………………………(10分)
∵ ME∥y轴,∴ ![]() .…………………………(11分)
.…………………………(11分)
∵ ![]() ,
,
∴ ![]() .…………………………(12分)
.…………………………(12分)
∴ ![]() .…………………………(13分)
.…………………………(13分)
∵ ![]() ,
,
∴ ⊙M与⊙A外切.…………………………(14分)
25、(14分)
解:(1)△AEF是等边三角形.………………………(2分)
由折叠过程易得:![]() ………………………(4分)
………………………(4分)
∵BC∥AD,∴![]() ………………………(6分)
………………………(6分)
∴△AEF是等边三角形. ………………………(7分)
(2)不一定. …………………………(8分)
当矩形的长恰好等于等边△AEF的边AF时,
即矩形的宽∶长=AB∶AF=sin60°=![]() 时正好能折出.……………(10分)
时正好能折出.……………(10分)
如果设矩形的长为a,宽为b,
可知当![]() 时,按此法一定能折出等边三角形;……………………(12分)
时,按此法一定能折出等边三角形;……………………(12分)
当![]() 时,按此法无法折出完整的等边三角形.………………(14分)
时,按此法无法折出完整的等边三角形.………………(14分)
〔第(1)小题其余证法一:〕
由平行线分线段定理知PE=PA, ∴ ![]() 是Rt
是Rt![]() 斜边上的中线.
斜边上的中线.
∴ ![]() ,∠1=∠3.
,∠1=∠3.
又∵ PN∥AD,∴ ∠2=∠3. 而2∠1+∠2=90°,∴ ∠1=∠2=30°,
在Rt![]() 中,∠1+∠AEF=90°,
中,∠1+∠AEF=90°,
∴ ∠AEF=60°,∠EAF=∠1+∠2=60°. ∴ △AEF是等边三角形.
〔第(1)小题其余证法二:〕
∵
△ABE与![]() 完全重合, ∴ △ABE≌
完全重合, ∴ △ABE≌![]() ,∠BAE=∠1.
,∠BAE=∠1.
由平行线等分线段定理知![]() . 又
. 又 ![]() ,
,
∴ ![]() ≌
≌![]() ,AE=AF.
,AE=AF. ![]() .
.
∴ △AEF是等边三角形.