初中毕业考试数学试卷
数 学 试 卷
（全卷三个大题，共22个小题；考试时间120分钟；满分：120分）
| 题 号 | 一 | 二 | 三 | 总 分 |
| 得 分 |
注意：考生可将《2006年云南省高中（中专）招生考试说明与复习指导·数学手册》及科学计算器（品牌和型号不限）带入考场使用.
| 得分 | 评卷人 |
|
|
|
一、填空题（本大题共6个小题，每小题3分，满分18分）
1．－2的绝对值= ．
2．生物学家发现一种病毒的长度约为0.00054mm，用科学计数法表示0.00054的结果为
．
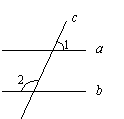
3．如图，已知直线a∥b，直线c与a、b相交，
若∠2＝114°，则∠1＝ ．
4．分解因式x3－x＝ ．
5．函数
中，自变量
的取值范围是
．
6．将两块直角三角尺的直角顶点重合为
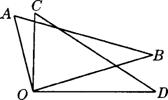如图的位置，若∠AOD=11O°，
则∠COB= ．
| 得分 | 评卷人 |
|
|
|
二、选择题（本大题共8个小题，每小题只有一个正确选项，每小题4分，满分32分）
7．下列运算正确的是（ ）
A．
B．(a2)3=a5 C．
D．
8．若a>0，则点P(-a，2)应在（ ）
A．第一象限内 B．第二象限内 C．第三象限内 D．第四象限内
9．用换元法解分式方程
时，如果设
，那么将原方程化为关于y的一元二次方程的一般形式是（ ）
A．
B．
|
|
D．
|
|
|
10．如图，⊙O的直径为10，圆心O到弦AB的距离
OM的长为3，则弦AB的长是（ ）
A．4 B．6 C．7 D．8
11．已知⊙O的半径为r，圆心O到直线l的距离为d．若直线l与⊙O有交点，则下列结论正确的是（ ）
A．d＝r B．d≤r C．d≥r D．d＜r
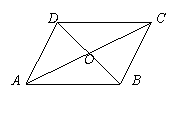12．如图，
ABCD中，对角线AC和BD相交于点O，如果
AC=12、BD=10、AB=m，那么m的取值范围是（ ）
A．10＜m＜12 B．2＜m＜22
C．1＜m＜11 D．5＜m＜6
13．一个扇形的圆心角是120°，面积为3πcm2，那么这个扇形的半径是（ ）
A．
cm B．3cm C．6cm D．9cm
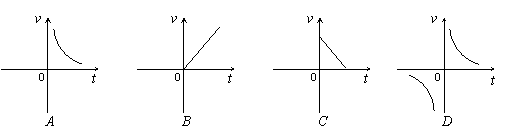14．在匀速运动中，路程s(千米)一定时，速度v(千米/时)关于时间t(小时)的函数关系的大致图象是（ ）
| 得分 | 评卷人 |
|
|
|
三、解答题（本大题共8个小题，满分70分）
| 得分 | 评卷人 |
15．（本小题6分）解方程组：
| 得分 | 评卷人 |
16．（本小题6分） 已知两个分式：A=
，B=
，其中
．下面有三个结论：
①A=B； ②A、B互为倒数； ③A、B互为相反数．
请问哪个正确?为什么?
| 得分 | 评卷人 |
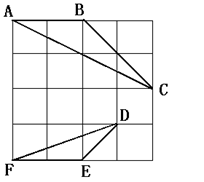
17．（本小题8分）如图，在4×4的正方形方格中，△ABC 和△DEF的顶点都在边长为1的小正方形的顶点上．
（1） 填空：∠ABC= °，BC= ；
（2） 判断△ABC与△DEF是否相似，并证明你的结论．
 |
| 得分 | 评卷人 |
18．（本小题8分）某公司开发出一种新产品，前期投入的开发、广告宣传费用共5000元，且每售出一套产品，公司还需支付产品安装调试费用20元．
（1）试写出总费用y(元)与销售套数x(套)之间的函数关系式；
（2）如果每套定价70元，公司至少要售出多少套产品才能确保不亏本？
| 得分 | 评卷人 |
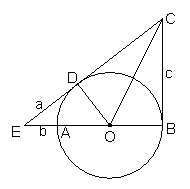
19．（本小题10分）如图,AB是⊙O的直径,CB、CE分别切⊙O于点B、D，CE与BA的延长线交于点E,连结OC、OD．
（1）求证：△OBC≌△ODC；
（2）已知DE=a，AE=b，BC=c，请你思考后，选用以上适当的数，设计出计算⊙O半径r的一种方案：
①你选用的已知数是
；
②写出求解过程．（结果用字母表示）
| 得分 | 评卷人 |
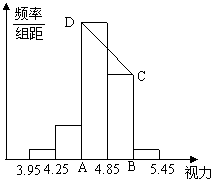20．（本小题10分）青少年视力水平的下降已经引起全社会的关注，某校为了了解初中毕业年级500名学生的视力情况，从中抽查了一部分学生视力，通过数据处理，得到如下频率分布表和频率分布直方图：
| 分 组 | 频 数 | 频 率 |
| 3.95～4.25 | 2 | 0.04 |
| 4.25～4.55 | 6 | 0.12 |
| 4.55～4.85 | 25 | |
| 4.85～5.15 | ||
| 5.15～5.45 | 2 | 0.04 |
| 合 计 | 1.00 |
请你根据给出的图表回答：
（1）填写频率分布表中未完成部分的数据；
（2）在这个问题中，总体是 ，
样本容量是 ．
（3）在频率分布直方图中梯形ABCD的面积是 ；
（4）请你用样本估计总体，可以得到哪些信息（写一条即可）
．
| 得分 | 评卷人 |
21．（本小题10分）阅读下列材料，并解决后面的问题．
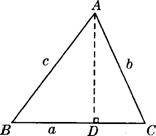在锐角△ABC中，∠A、∠B、∠C的对边分别是a、b、c．
过A作AD⊥BC于D（如图），
则 sinB=
，sinC=
，
即AD=csinB，AD=bsinC，
于是csinB=bsinC，
即
．
同理有
，
．
所以 
………(*)
即：在一个三角形中，各边和它所对角的正弦的比相等．
（1）在锐角三角形中，若已知三个元素a、b、∠A，运用上述结论(*)和有关定理就可以求出其余三个未知元素c、∠B、∠C，请你按照下列步骤填空，完成求解过程：
第一步：由条件 a、b、∠A 
∠B；
第二步：由条件 ∠A、∠B ∠C；
第三步：由条件 c．
（2）如图，已知：∠A=60°，∠C=75°，a=6，运用上述结论(*)试求b．
 |
| 得分 | 评卷人 |
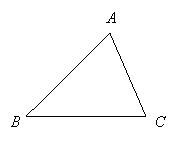
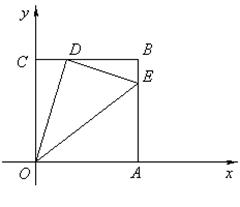
22．（本小题12分）如图，边长为4的正方形OABC的顶点O为坐标原点，点A在x轴的正半轴上，点C在y轴的正半轴上．动点D在线段BC上移动（不与B，C重合），连接OD，过点D作DE⊥OD，交边AB于点E，连接OE．
（1）当CD=1时，求点E的坐标；
（2）如果设CD=t，梯形COEB的面积为S，那么是否存在S的最大值？若存在，请求出这个最大值及此时t的值；若不存在，请说明理由．
初中毕业考试数学试卷参考答案
一、填空题（本大题共6个小题，每小题3分，满分18分）
1. 2 2. 5.4×10-4 3. 66° 4. x (x+1)( x -1) 5. x≥2 6. 70°
二、选择题（本大题共8个小题，每小题只有一个正确选项，每小题4分，满分32分）
7. D 8. B 9. A 10. D 11.B 12. C 13. B 14. A
三、解答题（本大题共8个小题，满分70分）
15．（本小题6分）
16．（本小题6分）因为 B=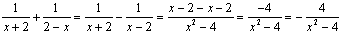
比较可知，A与B只是分式本身的符号不同，所以A、B互为相反数．
17．（本小题8分）
（1）∠ABC=135°, BC=
；
（2）能判断△ABC与△DEF相似（或△ABC∽△DEF）
这是因为∠ABC =∠DEF = 90°+45°=135° , 
，
∴ 
∴△ABC∽△DEF.
18．（本小题8分）
(1) 解：y＝5000＋20x
(2) 解法1：设公司至少要售出x套产品才能确保不亏本，则有：
70 x≥5000＋20x 解得：x≥100
解法2：每套成本是
若每套成本和销售价相等则：
解得： x＝100 因此公司至少要售出100套产品才能确保不亏本
19．（本小题10分）
（1）证明：∵CD、CB是⊙O的切线，
∴∠ODC=∠OBC=90°
又∵ OD=OB，OC=OC，
∴△OBC≌△ODC（HL）
（2）①选择a、b、c，或其中2个均给分；
②若选择a、b：由切割线定理：a2=b(b+2r) ，得r=
.
若选择a、b、c：
方法一：在Rt△EBC中，由勾股定理：(b+2r)2+c2=(a+c)2，得r=
.
方法二：Rt△ODE∽Rt△CBE，
，得r=
.
方法三：连结AD，可证：AD//OC，
，得r=
.
若选择a、c：需综合运用以上的多种方法，得r=
.
若选择b、c，则有关系式2r3+br2－bc2=0.
（以上解法仅供参考，只要解法正确均给分）
20．（本小题10分）
⑴第二列从上至下两空分别填15、50；第三列从上至下两空分别填0.5、0.3
⑵500名学生的视力情况，50 ⑶0.8
⑷本题有多个结论，只要是根据频率分布表或频率分布直方图的有关信息，并且用样本估计总体所反映的结论都是合理的．例如，该校初中毕业年级学生视力在4.55～4.85的人数最多，约250人；该校初中毕业年级学生视力在5.15以上的与视力在4.25以下的人数基本相等，各有20人左右等．
21．（本小题10分）
(1) 第一步：
；
第二步：∠A +∠B +∠C =180°；
第三步：a、∠A、∠C或b、∠B、∠C， 
或
(2)由三角形内角和定理可知∠B=180°-60°-75°=45°
所以，由
得 
即：
解得
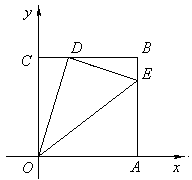22．（本小题12分）
解：(1) 正方形OABC中，因为ED⊥OD，即∠ODE =90°
所以∠CDO+∠EDB=90°，即∠COD=90°-∠CDO，而 ∠EDB =90°-∠CDO，
所以∠COD =∠EDB 又因为∠OCD=∠DBE=90°
所以△CDO∽△BED，
所以
，即
，得BE=
，
则：
因此点E的坐标为（4，
）．
(2) 存在S的最大值．
由△CDO∽△BED，
所以
，即
，BE=t－
t2，
×4×(4＋t－t2)
．
故当t=2时，S有最大值10．