中考数学模拟试卷 (1)
(华东师大版)
时间:120分钟 满分:150
一、选择题(本题共10小题,每题4分,共40分. 在每题所给出的四个选项中,只有一项是符合题意的. 把所选项前的字母代号填在题后的括号内.)
1.我国“杂交水稻之父”袁隆平主持研究的某种超级杂交稻平均亩产820千克。某地今年计划栽插这种超级水稻3000亩,预计该地今年收获这种超级杂交稻的总产量(用科学记数法表示)是( )
A.2.5×106千克 B. 2.46×106千克 C.2.5×105千克 D.2.46×105千克
2.观察下面图案,在A、B、C、D四幅图案中,能通过图案(1)的平移得到的是( )

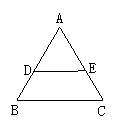
3.如图,DE是ΔABC的中位线,则ΔADE与ΔABC的面积之比是( )
A.1:1 B.1:2 C.1:3 D.1:4
 4.如图是一块手表,早上8时的时针、分针的位置如图所示,那么分针与时针所成的角的度数是( )
4.如图是一块手表,早上8时的时针、分针的位置如图所示,那么分针与时针所成的角的度数是( )
A. 120° B.80° C.60° D.150°
5.在下列图形中,既是中心对称图形又是轴对称图形的是 ( )
A.等腰三角形 B.圆 C.梯形 D.平行四边形
6.把分式方程![]() 的两边同时乘以(x-2), 约去分母,得( )
的两边同时乘以(x-2), 约去分母,得( )
A.1-(1-x)=1 B.1+(1-x)=1 C.1-(1-x)=x-2 D.1+(1-x)=x-2
7.相交两圆的公共弦长为16cm,若两圆的半径长分别为10cm和17cm,则这两圆的圆心距为( )
A.21cm B.16cm C.7cm D.27cm
8.小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车。车修好后,因怕耽误上课,他比修车前加快了骑车速度匀速行驶。下面是行驶路程s(米)关于时间t(分)的函数图像,那么符合这个同学行驶情况的图像大致是 ( )
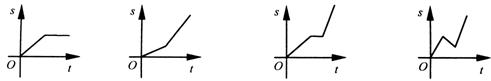 |
(A) (B) (C) (D)
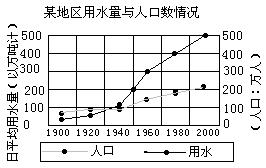 9.右图是某地区用水量与人口数情况统计图.日平均用水量为400万吨的那一年,人口数大约是( )
9.右图是某地区用水量与人口数情况统计图.日平均用水量为400万吨的那一年,人口数大约是( )
A.180万 B.200万
C.300万 D.400万
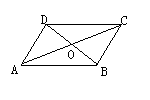 10.如图,
10.如图,![]() ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取什范围是
ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取什范围是
A. 2<m<22 B.1<m<11
C.10<m<12 D.5<m<6
二、填空题(本题共有5小题,每题4分,共20分.请把结果直接填在题中的横线上.)
11.分解因式:a3-a= 。
12.一个多边形的每个外角都等于30°,这个多边形的内角和为_________度。
13.已知方程x2+(2k+1)x+k2-2=0的两实根的平方和等于11,k的取值是 。
 14.亮亮想制作一个圆锥模型,这个模型的侧面是用一个半径为9cm,圆心角为240°的扇形铁皮制作的,再用一块圆形铁皮做底。请你帮他计算这块铁皮的半径为________cm。
14.亮亮想制作一个圆锥模型,这个模型的侧面是用一个半径为9cm,圆心角为240°的扇形铁皮制作的,再用一块圆形铁皮做底。请你帮他计算这块铁皮的半径为________cm。
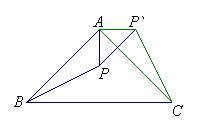
15.如图ABC是等腰直角三角形,BC是斜边,将△ABP 绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,那么PP′有长等于____________。
三、(本题有2小题,每题8分,共16分)
16. 先化简,后求值:![]() ,其中x=2.
,其中x=2.
17.已知反比例函数![]() 与一次函数
与一次函数![]() 的图像的一个交点的纵坐标是
-4,求
的图像的一个交点的纵坐标是
-4,求![]() 的值.
的值.
四、(本题有2小题,每题8分,共16分)
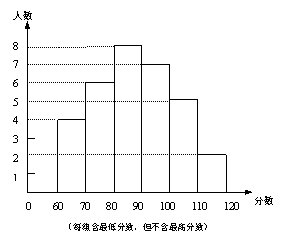 18.
18.![]() 某中学部分同学参加全国初中数学竞赛,取得了优异的成绩,指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了频率分布直方图。
某中学部分同学参加全国初中数学竞赛,取得了优异的成绩,指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了频率分布直方图。
请回答:
(1)该中学参加本次数学竞赛的有多少名同学?
(2)如果成绩在90分以上(含90分)的同学获奖,那么该中学参赛同学的获奖率是多少?
(3)图中还提供了其它信息,例如该中学没有获得满分的同学等等。请再写出两条信息。
19.某工程队(有甲、乙两组)承包我市新区某路段的路基改造工程,规定若干天内完成.已知甲组单独完成这项工程所需时间比规定时间的2倍多4天,乙组单独完成这项工程所需时间比规定时间的2倍少16天.如果甲、乙两组合做24天完成,那么甲、乙两组合做能否在规定时间内完成?
五、(本题有2小题,每题10分,共20分)
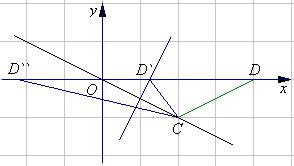
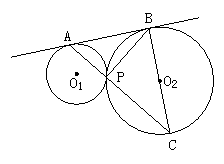 20.如图,⊙O1与⊙O2外切于点P,外公切线AB切⊙O1于点A,切⊙O2于点B,
20.如图,⊙O1与⊙O2外切于点P,外公切线AB切⊙O1于点A,切⊙O2于点B,
(1)求证:AP⊥BP;
(2)若⊙O1与⊙O2的半径分别为![]() 和
和![]() ,求证:
,求证:![]() ;
;
(3)延长AP交⊙O2于C,连结BC,若![]() ,求
,求![]() 的值。
的值。
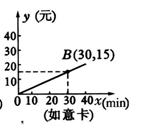
21.为发展电信事业,方便用户,电信公司对移动电话采取不同的收费方式,其中,所使用的“便民卡”与“如意卡”在某市范围内每月(30天)的通话时间![]() (min)与通话费y(元)的关系如图所示:
(min)与通话费y(元)的关系如图所示:
(1)分别求出通话费![]() 、
、![]() 与通话时间
与通话时间![]() 之间的函数关系式;
之间的函数关系式;
(2)请帮用户计算,在一个月内使用哪一种卡便宜?

六、(本题有2小题,22题14分,23题12分,共26分)
22.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
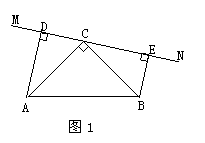
(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE;
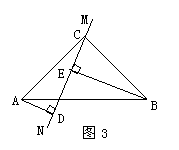
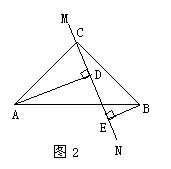 (3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
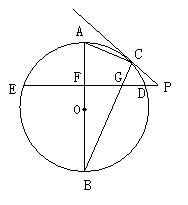 23.如图,AB是⊙O的直径,BC是⊙O的弦,⊙O的割线PDE垂直AB于点F,交BC于点G,连结PC,∠BAC=∠BCP,求解下列问题:
23.如图,AB是⊙O的直径,BC是⊙O的弦,⊙O的割线PDE垂直AB于点F,交BC于点G,连结PC,∠BAC=∠BCP,求解下列问题:
(1)求证:CP是⊙O的切线。
(2)当∠ABC=30°,BG=![]() ,CG=
,CG=![]() 时,求以PD、PE的长为两根的一元二次方程。
时,求以PD、PE的长为两根的一元二次方程。
(3)若(1)的条件不变,当点C在劣弧AD上运动时,应再具备什么条件可使结论BG2=BF·BO成立?试写出你的猜想,并说明理由。
七、本题12分
24.已知二次函数![]() 当b取任何实数时,它的图象是一条抛物线.
当b取任何实数时,它的图象是一条抛物线.
(1)现在有如下两种说法:
①b取任何不同的数值时,所对应的抛物线都有着完全相同的形状;
②b取任何不同的数值时,所对应的抛物线都有着不相同的形状;你认为哪一种说法正确,为什么?
(2)若取b= -1,b=2时对应的抛物线的顶点分别为A、B,请你求出AB的解析式,并判断:当b取其它实数值时,所对应的抛物线的顶点是否在这条直线上?说明理由.
(3)在(2)中所确定的直线上有一点C且点C的纵坐标为-1,问在x轴上是否存在点D使△COD为等腰三角形,若存在直接写出点D坐标;若不存在,简单说明理由.
参考答案:
一、选择题
1.B.820×3000==2.46×106 。
2.C.根据平移的定义,比较这四个图形即得。
3.D.面积比等于相似比的平方。
4.A.![]()
5.B.在这四个图形中,只有圆既是中心对称图形又是轴对称图形。
6.D.![]() 两边同乘x-2即得。
两边同乘x-2即得。
7.A.两圆的圆心距为:![]()
8.C.小明的上学过程实际上分为三段:一开始的正常速度匀速行驶,中间的修车和车修好后,因怕耽误上课,他比修车前加快了骑车速度匀速行驶故选C。
9.A.先从图上找到日平均用水量为400万吨的那一年所对应的点,过此点作垂线,则可在图中的人口曲线上找到相应的点,即为那一年所对应的大约的人口数。
10.B.在△ABO中,OA=6,0B=5,由三角形的两边之和大于第三边即得。
二、填空题
11.![]()
12.18000 。由多边形的每个外角都等于30°可得它的内角都等于1500,又这个多边形的边数为![]() 所以这个多边形的内角和为12×1500=18000。
所以这个多边形的内角和为12×1500=18000。
13.k=1。因为△=![]()
又知x12+x22=11,即(x1+x2)2-2x1x2=11,又x1+x2=-(2k+1),x1×x2=k2-2,所以〔-(2k+1)〕2-2(k2-2)=11,解得:k=-3,k=1。故k=1。
14.6.圆锥的底面周长为![]() ,设底面半径为r,则2πr=12π,所以r=6。
,设底面半径为r,则2πr=12π,所以r=6。
15.![]() 由∠PAP,=900,PP,=
由∠PAP,=900,PP,=![]()
16.解:![]() ,……6分
,……6分
当x=2时,![]() =2×2-1=3。………………………………………………8分
=2×2-1=3。………………………………………………8分
17.解:根据题意有
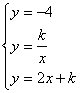 ,………………………………………………………………………………4分
,………………………………………………………………………………4分
所以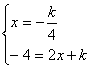 ………………………………………………………………………6分
………………………………………………………………………6分
解得![]() .……………………………………………………………………………8分
.……………………………………………………………………………8分
18.解:(1)4+6+8+7+5+2=32人…………………………………………………………………2分
(2)90分以上人数:7+5+2=14人
![]() ………………………………………………………………5分
………………………………………………………………5分
(3)该中学参赛同学的成绩均不低于60分。成绩在80—90分数的人数最多。…8分
19.解:设规定的时间是![]() 天,则甲组单独完成所需要的时间是
天,则甲组单独完成所需要的时间是![]() 天,乙组单独完成所需的时间是
天,乙组单独完成所需的时间是![]() 天,可得:
天,可得:
![]() ,……………………………………………………………3分
,……………………………………………………………3分
解得:![]() ,………………………………………………………………5分
,………………………………………………………………5分
经检验![]() 不符合题意,舍去.……………………………………………………7分
不符合题意,舍去.……………………………………………………7分
所以规定的时间是28天,它们两组能够在规定的时间内完成这项工作.………8分
20.证明:(1)∵∠BPC为⊙O2的直径BC所对的圆周角…………
∴∠BPC=90°
即AP⊥BP……………………………………………………………………………………3分
(2)连结O1A、O1 P、O2 P,
∵∠APO1=∠CPO2
∴△APO1∽△CPO2…………………………………………………………………………4分
∴![]() (1)………………………………………………………………5分
(1)………………………………………………………………5分
∵△ABP∽△BPC
∴![]()
![]()
∴![]() (2)………………………………………………………………7分
(2)………………………………………………………………7分
将(2)代入(1)得:![]() ……………………………………………………8分
……………………………………………………8分
(3)∵![]() =
=![]() ,
,![]()
∴![]() =
=![]() ………………………………………………………………10分
………………………………………………………………10分
21.解: (1)![]()
![]() ………………………………4分
………………………………4分
(2)当![]() 时,
时,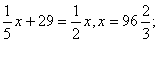 ………………………………6分
………………………………6分
当![]() 时,
时,![]() …………………………………8分
…………………………………8分
所以,当通话时间等于96![]() min时,两种卡的收费一致;当通话时间小于
min时,两种卡的收费一致;当通话时间小于![]() mim时,“如意卡便宜”;当通话时间大于
mim时,“如意卡便宜”;当通话时间大于![]() min时,“便民卡”便宜。……10分
min时,“便民卡”便宜。……10分
22.解. (1) ① ∵∠ACD=∠ACB=90°
∴∠CAD+∠ACD=90°
∴∠BCE+∠ACD=90°
∴∠CAD=∠BCE ……………… 2分
∵AC=BC
∴△ADC≌△CEB ……………… 3分
② ∵△ADC≌△CEB
∴CE=AD,CD=BE
∴DE=CE+CD=AD+BE ……………… 4分
(2) ∵∠ADC=∠CEB=∠ACB=90°
∴∠ACD=∠CBE ……………… 5分
又∵AC=BC
∴△ACD≌△CBE ……………… 7分
∴CE=AD,CD=BE
∴DE=CE-CD=AD-BE ……………… 9分
(3) 当MN旋转到图3的位置时,AD、DE、BE所满足的等量关系是DE=BE-AD(或AD=BE-DE,BE=AD+DE等) ……………… 11分
∵∠ADC=∠CEB=∠ACB=90°
∴∠ACD=∠CBE,
又∵AC=BC, ……………… 12分
∴△ACD≌△CBE, ……………… 13分
∴AD=CE,CD=BE,
∴DE=CD-CE=BE-AD. ……………… 14分
 23.解。(1) 连结OC,
23.解。(1) 连结OC,
∵∠A+∠B=90°,∠0CB=∠B,∠BAC=∠BCP
∴∠OCP=∠OCB+∠BCP=∠A+∠B=90°。……2分
∴ CP是⊙O的切线。…………………………3分
(2)∵∠B=30° ∴∠A=∠BGP=60°
∴∠BCP=∠BGP=60°
∴ΔCPG是正三角形.…………4分
∴PG=CP=![]() ………………………5分
………………………5分
∵PC切⊙O于C
∴PC2=PD·PE=![]() ……6分
……6分
又∵BC=![]()
∴AB=6,FD=![]() ,EG=
,EG=![]() …………………7分
…………………7分
∴PD=2![]()
∴PD+PE=![]() …………………8分
…………………8分
∴以PD、PE为两根的一元二次方程为x2-48x+10![]() =0……………9分
=0……………9分
(3)当G为BC中点,OG⊥BC,OG∥AC或∠BOG=∠BAC…时,结论BG2=BF·BO成立。要让此结论成立,只要证明ΔBFG∽ΔBGO即可,凡是能使ΔBFG∽ΔBGO的条件都可以。…12分
24.解:(1)抛物线的形状和开口方向只决定于二次项系数的值,与一次项的系数、常数项无关.所以①的说法是正确的。………………………………………………………3分
(2)当b= -1时,顶点坐标是A(![]() ,
,![]() );……………………………………5分
);……………………………………5分
当b= 2时,顶点坐标是B(![]() ,
,![]() ),所以直线AB的解析式是
),所以直线AB的解析式是![]() .……7分
.……7分
二次函数![]() 的顶点坐标可以表示为(
的顶点坐标可以表示为(![]() ,
,![]() ),它们始终在直线
),它们始终在直线![]() 上.…………………………………………………………………………9分
上.…………………………………………………………………………9分
(3)如图,存在三个满足条件的点,它们的坐标分别是(4,0),(![]() ,0),(
,0),(![]() ,0).…………………………………………………………………………………………12分
,0).…………………………………………………………………………………………12分