中考数学模拟试题（一）
数学试卷
（考试时间90分钟，满分100分）
一、选择题：（每题3分，共24分）
1、-3的相反数是
A、-3
B、3
C、-
D、
2、深圳市某中学环保小组星期六上街开展环保宣传活动，其中十位同学负责收集废电池，每人收集到的废电池分别为5、7、3、4、9、4、6、7、6、4，则这一组数据的众数是
A、4 B、5 C、6 D、7
3、点P（-3，3）关于原点对称的点的坐标是
A、（-3，-3） B、（-3，3） C、（3，3） D、（3，-3）
4、将多项式x2-3x-4分解因式，结果是
A、（x-4）（x+1） B、（x-4）（x-1） C、（x+4）（x+1） D、（x+4）（x-1）
5、正五边形的内角是
A、180º B、360º C、540º D、720º
6、下列两个三角形不一定相似的是
A、两个等边三角形 B、两个全等三角形
C、两个直角三角形 D、两个顶角是120º的等腰三角形
7、化简二次根式
，结果是
A、
B、
C、
D、
8、反比例函数y=
在第一象限内的图象如图，点M是图象上一点，MP垂直x轴于
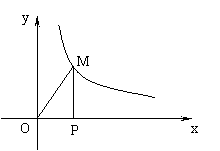点P，如果△MOP的面积为1，那么k的值是
A、1 B、2 C、4
D、
二、填空题：（每题3分，共12分）
9、中国足球队44年来首次进入世界杯决赛圈，与巴西、土尔其、哥撕达黎加队同分在C组。6月3日，某班40名同学就C组哪支队将以小组第二名的身份进入十六强进行了竞猜，统计结果如图。若认为中国队以小组第二的身份进入十六强的同学人数作为一组的频数，则这一组的频率为__________。
 |
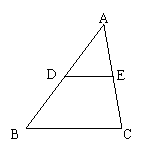10、如图，D、E分别是△ABC的边AB、AC的中点，若S△ADE=1，则S△ABC=____。
11、深圳经济稳步增长，根据某报6月7日报道：我市今年前五个月国内生产总值为770亿元，比去年前五个月国内生产总值增长13.8%。设去年前五个月国内生产总值为x亿元，根据题意，列方程为
___________________。
12、如果实数a、b满足(a+1)2=3-3(a+1)，3(b+1)=3-(b+1)2，那么
的值为_______。
三、解答题：（第13、14、15题每题6分，第16、17题每题8分，第18、19、20题每题10分，共64分）
13、计算：
14、解方程：
15、作图题（要求用直尺和圆规作图，保留作图痕迹，不要求写出证明过程）
已知：圆（如图）
求作：一条线段，使它把已知圆分成面积相等的两部分。
作法：
16、已知：如图，在口ABCD中，E、F是对角线AC上的两点，且AF=CE。
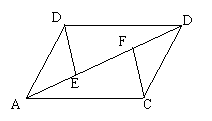求证：DE=BF
17、我国很多城市水资源缺乏，为了加强居民的节水意识，合理利用水资源，很多城市制定了用水收费标准。A市规定了每户每月的标准水量，不超过标准用水量的部分每立方米1.2元收费；超过标准用水量的部分按每立方米3元收费。该市张大爷家5月份用水9立方米，需交费16.2元，A市规定的每户每月标准用水量是多少立方米？
18、阅读材料，解答问题
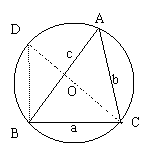
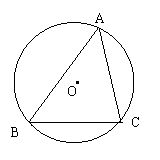
命题L如图，在锐角△ABC中，BC=a、CA=c、AB=c，△ABC的外接圆半径为R，则
。
证明：连结CO并延长交⊙O于点D，连结DB，则∠D=∠A
∵CD为⊙O的直径，∴∠DBC=90º
在Rt△DBC中
∵
∴sinA=
，即
同理
、
∴
请你阅读前面所给的命题及证明后，完成下面（1）、（2）两小题
（1）前面的阅读材料中略去了“和”的证明过程，请你把“”的证明过程补写出来。
（1） （2）
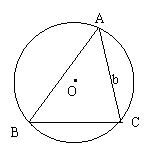
（2）直接用前面阅读材料中命题的结论解题
已知，如图，在锐角△ABC中，BC=
，CA=
，∠A=60º，求△ABC的外接圆的半径R及∠C。
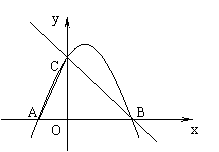
19、已知：如图，直线y=-x+3与x轴、y轴分别交于点B、C，抛物线y=-x2+bx+c经过点B、C，点A是抛物线与x轴的另一个交点。
（1）求抛物线的解析式。
（2）若点P在直线BC上，且S△PAC=S△PAB，求点P的坐标。
 |
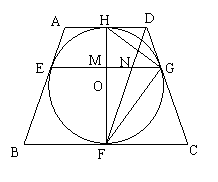
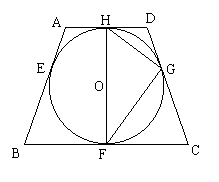
20、如图，等腰梯形ABCD中，AD//BC，AB=DC，以HF为直径的⊙O与AB、BC、CD、DA相切，切点分别是E、F、G、H，其中H为AD的中点，F为BC的中点，连结HG、GF。
（1）若HG和GF的长是关于x的方程x2-6x+k=0的两个实数根，求⊙O的直径HF（用含k的代数式表示），并求出k的取值范围。
 | |||
 | |||
（1） （2）
（2）如图，连结EG、DF，EG与HF交于点M，与DF交于点N，求
的值。
厦门市2007年中考模拟试题（一）参考答案
一、选择题：BADAC CBB
二、填空题：
9、0.4 10、4 11、(1+13.8%)x=770 12、2或23
三、解答题：
13、
14、x1=1，x2=-2
15、略
16、略
17、设A市规定的每户每月标准水量是x立方米
∵9×1.2=10.8<16.2
∴张大爷5月份用水量超过了月标准用水量
则依题意有 1.2x+(9-x)×3=16.2
x=6
18、①略 ②75º
19、①y=-x2+2x+3 ②（1，2）、（-3，6）
20、①∵HF是⊙O的直径，∴△HGF是Rt△
∴HF2=HG2+GF2=(HG+GF)2-2HG×GF
由根与系数的关系：HG+GF=6 HG×GF=k
∴HF2=62-2k
∵HF>0 ∴HF=
∵方程x2-6x+k=0有两根
∴△=62-4k≥0
又k=HG×GF≥0，且36-2k≥0
∴0≤k≤9
②∵F是BC的中点，H是AD的中点
由切线长定理得 AE=AH=HD=DG EB=BF=FC=CG
∴AE：EB=DG：GC ∴AD//EG//BC
∵AD⊥HF ∴GE⊥HF
设DG=DH=a，CG=CF=b
∴AD//EG//BC
∴NG：FC=DG：DC 即MN:b=a:(a+b)
MN:HD=NF:DF=CG:DC 即MN:a=b:(a+b)
∴NG=MN ∴GN：NE=1：3