初中毕业和高中阶段各类学校招生考试
数 学 试 题
（全卷满分:150分;答卷时间:120分钟）
考生须知：1．解答内容一律写在答题卡上，否则不得分.
2．答题、画线一律用0.5毫米的黑色签字笔.
一、选择题（本大题有7小题，每小题3分，共21分.每小题都有四个选项，其中有且只有一个选项是正确的）
1．下列计算正确的是
（A）·＝ (B) ＋＝
(C) ＝3 (D) ÷＝2
2．已知在⊙O中，弦AB的长为8厘米,圆心O到AB的距离为3厘米, 则⊙O的半径是
（A）3厘米 (B) 4厘米
(C) 5厘米 (D) 8厘米
3．已知：如图1, ⊙O的两条弦AE、BC相交于点D,连结AC、
BE.若∠ACB＝60°,则下列结论中正确的是
（A） ∠AOB＝60° (B) ∠ADB＝60°
(C) ∠AEB＝60° (D) ∠AEB＝30°
4．一定质量的干松木,当它的体积V＝2m3时,它的密度ρ＝
0.5×103kg/m3,则ρ与V的函数关系式是
（A） ρ＝1000V (B) ρ＝V＋1000
(C) ρ＝ (D) ρ＝
5．矩形ABCD中的顶点A、B、C、D按顺时针方向排列,若在平面直角坐标系内, B、D 两点对应的坐标分别是（2, 0）, (0, 0),且 A、C两点关于x轴对称.则C 点对应的坐标是
（A）（1, 1） (B) （1, －1）
(C) （1, －2） (D) （, －）
6．已知：如图2，△ABC中，P为AB上一点，在下列四个条件中：
①∠ACP＝∠B；②∠APC＝∠ACB；③AC2＝AP·AB；④AB·CP＝AP·CB，能满足△APC和△ACB相似的条件是( )
A．①②④ B．①③④
C．②③④ D．①②③
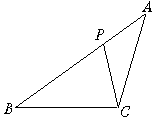
图2
7．如图3，将矩形ABCD沿着对角线BD折叠，使点C落在C′处，BC′交AD于E，下列结论不一定成立的是( )
A．AD＝BC′ B．∠EBD＝∠EDB
C．△ABE～△CBD D．sinABE＝
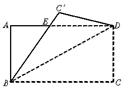
图3
二、填空题（本大题有10小题，每小题4分，共40分）
8．－3的相反数是 .
9．计算：sin30°＝ .
10．已知：∠A＝30°,则∠A的补角是_____度.
11．已知AD是△ABC的角平分线，E、F分别是边AB、AC的中点，连结DE、DF．在不再连结其他线段的前提下，要使四边形 AEDF成为菱形，还需添加一个条件，这个条件可以是______．
12．在⊙O1中，圆心角∠AOB的度数100°，则弦AB所对的圆周角的度数是______．
13．计算：3x2y＋2x2y＝ .
阅读下面一则材料，回答第14、15题：
A、B两点被池塘隔开，在AB外选一点C，连结AC和BC，并分别找出AC和BC的中点M、N，如果测得MN＝20 m，那么AB＝2×20 m＝40 m．
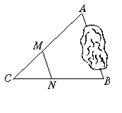
图4
14．也可由图5所求，用相似三角形知识来解，请根据题意填空：延长AC到D，使CD＝
AC，延长BC到E，使CE＝______，则由相似三角形得，AB＝______．
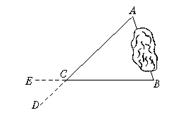
图5
15．还可由三角形全等的知识来设计测量方案，求出AB的长，请用上面类似的步骤，在图6中画出图形并叙述你的测量方案．
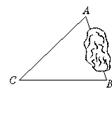
图6
16．两个不相等的无理数，它们的乘积为有理数，这两个数可以是______．
17．定义一种运算*，其规则为：当a≥b时，a*b＝b3；当a＜b时，a*b＝b2．根据这个规则，方程3*x＝27的解是______．
三、解答题（本大题有9小题，共89分）
18．（本题满分8分）
解不等式组 并把解集在数轴上表示出来.
19．（本题满分8分）如图7，⊙O表示一圆形纸板，根据要求，需通过多次剪裁，把它剪成若干个扇形面，操作过程如下：第1次剪裁，将圆形纸板等分为4个扇形；第2次剪裁，将上次得到的扇形面中的一个再等分成4个扇形；以后按第2次剪裁的作法进行下去．
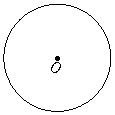
图7
(1)请你在⊙O中，用尺规作出第2次剪裁后得到的7个扇形(保留痕迹，不写作法)．
(2)请你通过操作和猜想，将第3、第4和第n次裁剪后所得扇形的总个数(S)填入下表．
| 等分圆及扇形面的次数(n) | 1 | 2 | 3 | 4 | … | n |
| 所得扇形的总个数(S) | 4 | 7 | … |
(3)请你推断，能不能按上述操作过程，将原来的圆形纸板剪成33个扇形？为什么？
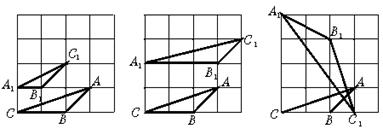
20．（本题满分8分）如图8，在大小为4×4的正方形方格中，△ABC的顶点A、B、C在单位正方形的顶点上.
（1）请在图中画一个△A1B1C1使△A2B2C2∽△ABC(相似比不为1)，且点A1、B1、C1都在单位正方形的顶点上．
（2）请在图中画一个△A2B2C2使△A2B2C2∽△ABC(相似比为1)，且点A2、B2、C2都在单位正方形的顶点上．
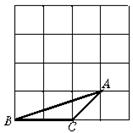
图8
21．（本题满分9分）某工厂现有甲种原料360千克，乙种原料290千克，计划利用这两种原料生产A、B两种产品，需要用甲种原料9千克，乙种原料3千克，可获利润700元；生产一件B种产品，需要甲种原料4千克，乙种原料10千克，可获利润1200元．
(1)按要求安排A、B两种产品的生产件数，有哪几种方案？请你设计出来．
(2)设生产A、B两种产品获总利润为y(元)，其中一种的生产件数为x，试写出y与x之间的函数关系式，并利用函数性质说明(1)中哪种生产方案获总利润最大？最大利润是多少？
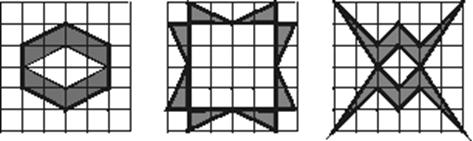
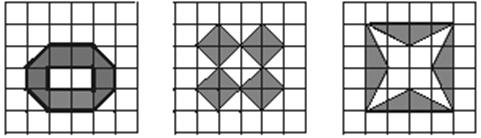
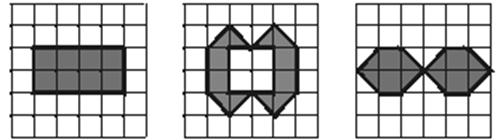
22．（本题满分10分）已知：图A、图B分别是6×6正方形网格上的两个轴对称图形（阴影部分），其面积分别为SA、SB（网格中最小的正方形面积为一个平方单位），请观察图形并解答下列问题．
（1）填空：SA︰SB的值是___________；
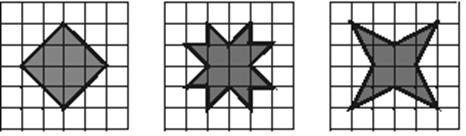
（2）请在图C的网格上画出一个面积为8个平方单位的中心对称图形；
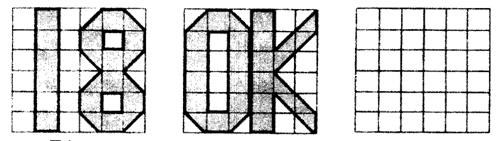
图A 图B 图C
23．（本题满分10分）如图9，在直角坐标系中，第一次将△OAB变换成△OA1B1，第二次将△OA1B1变成△OA2B2，第三次将△OA2B2变成△OA3B3．已知A(1，3)，A1(2，3)，A2(4，3)，
A3(8，3)；B(2，0)，B1(4，0)，B2(8，0)，B3(16，0)．
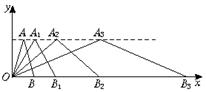
图9
(1)观察每次变换前后的三角形有何变化，找出规律，按此变换再将△OA3B3变成△OA4B4，则A4的坐标是______，B4的坐标是______．
(2)若按第(1)题找到的规律将△OAB进行了n次变换，得到△OAnBn，比较每次变换中三角形顶点坐标有何变化，找出规律，推测An的坐标是______，Bn的坐标是______．
24．（本题满分12分）已知x1、x2是一元二次方程4kx2-4kx＋k＋1＝0的两个实数根．
(1)是否存在实数k，使(2x1-x2)(x1-2x2)＝-
成立？若存在，求出k的值；若不存在请说明理由．
(2)求使
-2的值为整数的实数k的整数值．
25．(本题满分12分) 如图10，已知⊙O和⊙O′都经过点A和点B，直线PQ切⊙O于点P，交⊙O′于点Q、M，交AB的延长线于点N．
(1)求证：PN2＝NM·NQ．
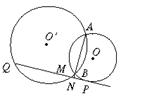
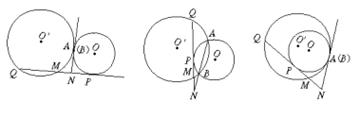
图10 图11 图12 图13
(2)若M是PQ的中点，设MQ＝x，MN＝y，求证：x＝3y．
(3)若⊙O′不动，把⊙O向右或向左平移，分别得到图11、图12、图13，请你判断(直接写出判断结论，不需证明)；
①(1)题结论是否仍然成立？
②在图11中，(2)题结论是否仍然成立？
在图12、图13中，若将(2)题条件改为：M是PN的中点，设MQ＝x，MN＝y，则x＝3y的结论是否仍然成立？
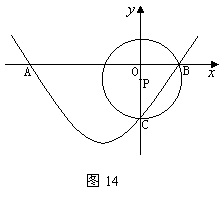
26．（本题满分12分）已知，如图14，抛物线
经过
轴上的两点A（
，0）、B（
，0）和轴上的点C（0，
），⊙P的圆心P在
轴上，且经过B、C两点，若
，AB=
，
（1）求抛物线的解析式；
（2）D在抛物线上，且C、D两点关于抛物线的对称轴对称，问直线BD是否经过圆心P？并说明理由；
（3）设直线BD交⊙P于另一点E，求经过点E的⊙P的切线的解析式。
 |
厦门市2007年初中毕业和高中阶段各类学校招生考试
数学试卷参考答案
一、选择题（本大题有7小题，每小题3分，共21分.每小题都有四个选项，其中有且只有一个选项是正确的）
1．A 2．C 3．C 4．D 5．B 6．D 7．C
二、填空题（本大题有10小题，每小题4分，共40分）
8．3 9．
10．150 11．AB＝AC 12．50°或130°
13． 5x2y 14.BC 2ED 15．延长AC至D，使AC＝CD，延长BC至E，使BC＝EC，则△ABC≌△DCE，∴ AB＝DE，量出DE即得AB．(图略)
16．
＋1和-1等 17．3
三、解答题（本大题有9小题，共89分）
18．解：解：解不等式(1)，得x≥2
解不等式(2)，得x≥3
∴不等式组的解集是：x≥3
19．解：①略 ②10，13，3n＋1 ③因为S＝33．
由②得3n＋1＝33，n＝10
．
因为n应为正整数，所以不能将原来的扇形纸片剪成33个扇形．
20．(1)由题设知，AB∶BC∶CA＝∶2∶
＝1∶∶
＝2∶2∶2＝……故可在图中作A1B1，B1C1＝，C1A1＝，或A1B1＝2，B1C1＝2，C1A1＝2或A1B1＝，B1C1＝，A1C1＝5……，
(2)本题只要全等即可，画法较多，图略．
21．解：(1)设安排生产A种产品x件，则生产B种产品为(50-x)件．
解这个不等式组得：30≤x≤32，而x为整数．
∴ x只能取30，31，32，相应的(50-x)的值为20，19，18．∴ 生产方案有三种：
第一种：生产A种产品30件，B种产品20件；
第二种：生产A种产品31件，B种产品19件；
第三种：生产A种产品32件，B种产品18件．
(2)设生产A种产品的件数为x，则生产B种产品的件数为(50-x)．
根据题意得，y＝700x＋1200(50-x)＝-500x＋60000，其中x只能取30，31，32．
∵ -500＜0，∴ 此一次函数y随x的增大而减小．
∴ 当x＝30时，y的值最大．即按第一种生产方案安排生产，获总利润最大，最大利润为：
-500×30＋60000＝45000(元)．
22．解：（1） （2）如图
23．(1)(16，3)，(32，0) (2)(2n，3)，(2n＋1，0)
24．解：(1)∵ k≠0，且Δ≥0，∴ k＜0，
又若(2x1-x2)(x1-2x2)＝-，则k＝
．
而k＜0，∴ 不存在实数k，使(2x1-x2)(x1-2x2)＝-成立．
(2)k的整数值为-2，-3，-5．
4．(1)
(2)k＜16且k≠0．
25．(1)略 (2)∵ PM＝MQ＝x，MN＝y，PN2＝MN·NQ，∴ (x-y)2＝y(x＋y)，整理，得x2＝3xy，∵ x≠0，∴ x＝3y．
(3)在图11、图12、图13中(1)题结论都成立，在图11中(2)题结论成立．在图12、图13中，按题意改变条件后，x＝3y的结论仍然成立．
26．解（1）依题意得
，则＋＝
，
＝
又∵∣－∣＝，即
＝
∴
，解得
∴抛物线的解析式为
（2）由（1）得抛物线
令＝0，则
，解得
，
∴A（
，0），B（
，0）
又C（0，），C、D两点关于直线＝
对称，∴D（，）
设经过B、D两点的直线解析式为
解得
，
∴
设⊙P与轴相交的另一点是M（0，
）圆心P（0，
）
则
，∴
，∴
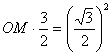，∴P（0，
）
∵点P（0，）的坐标满足
∴直线BD经过圆心P。
（3）设BD交⊙P于另一点E，过E作BF⊥轴于F得：△OPB≌△FPE
∴PF＝OP＝， ∴E（，－1）
设经过E的⊙P的切线为
，交轴于Q，则∠PEQ＝900，EF⊥PQ
∴
，即
，∴FQ＝
，Q（0，
）
设的解析式为
，∵经过点E、Q
∴
，
，∴
∴经过E点的⊙P的切线解析式是。