高中阶段学校招生考试数学试卷

高中阶段学校招生考试数学试卷

说明：本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共6页，满分130分，考试时间100分钟．

注意事项：

1．试卷的选择题和非选择题都在答题卡上作答，不能答在试卷上．

2．要作图（含辅助线）或画表，先用铅笔进行画线、绘图，再用黑色字迹的钢笔或签字笔描黑．

3．其余注意事项，见答题卡．

第Ⅰ卷（选择题　共30分）

一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的）．

1．计算的值是（　　）

Ａ．　　　　　 Ｂ．　　　　 Ｃ．　　　　　　　Ｄ．

2．下面简单几何体的左视图是（　　）

3．下列四个算式中，正确的个数有（　　）

①　　　　②　　　③　　　　④

Ａ．0个　　　　Ｂ．1个　　　　Ｃ．2个　　　　Ｄ．3个

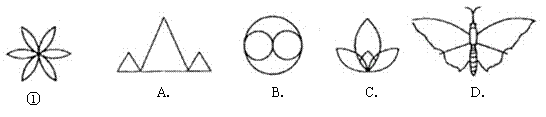
4．与平面图形有①有相同对称性的平面图形是（　　）

5．下列说法正确的是（　　）

A．无限小数是无理数　　　　　　　　　　　　　　 B．不循环小数是无理数

C．无理数的相反数还是无理数　　　　　　　 D．两个无理数的和还是无理数

6．小颖准备用21元钱买笔和笔记本．已知每支笔3元，每个笔记本2元，她买了4个笔记本，则她最多还可以买（　　）支笔．

A．1　　　　　　　B．2　　　　　　　C．3　　　　　　　D．4

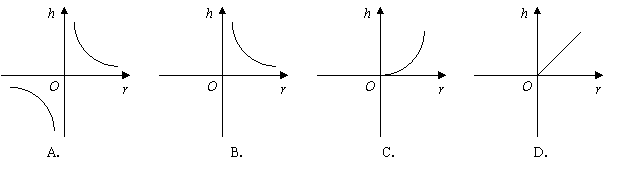
7．若为圆柱底面的半径，为圆柱的高．当圆柱的侧面积一定时，则与之间函数关系的图象大致是（　　）

8．观察下列图形，并判断照此规律从左向右第2007个图形是（　　）

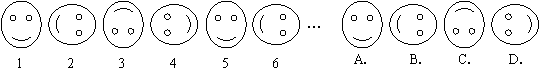
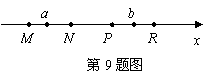
9．如图，分别是数轴上四个整数所对应的点，其中有一点是原点，并且．数对应的点在与之间，数对应的点在与之间，若，则原点是（　　）

A．或　　　　　B．或　　　　　C．或　　　　 D．或

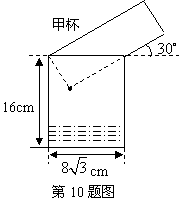10．如图，两个高度相等的圆柱形水杯，甲杯装满液体，乙杯是空杯．若把甲杯中的液体全部倒入乙杯，则乙杯中的液面与图中点的距离是（　　）

A．　　　　　　　B．　　　　　C．　　　　　　　　　　 D．

第Ⅱ卷（非选择题　共100分）

二、填空题（本大题共5小题，每小题3分，共15分．把答案填在答题卡中）．

11．佛山“一环”南线路段的304盏太阳能路灯一年大约可节电221920千瓦时，用科学记数法表示为　　　　　　  千瓦时（保留两个有效数字）．

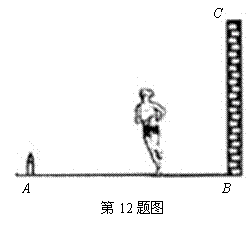
12．如图，地面处有一支燃烧的蜡烛（长度不计），一个人在与墙之间运动，则他在墙上投影长度随着他离墙的距离变小而　　　　  （填“变大”、“变小”或“不变”）．

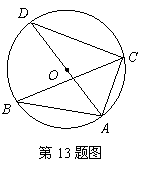
13．如图，内接于是的直径，，则　　　　度．

14．某班准备同时在两地开展数学活动，每位同学由抽签确定去其中一个地方，则甲、乙、丙三位同学中恰好有两位同学抽到去B地的概率是　　　　 ．

15．已知二次函数（是常数），与的部分对应值如下表，则当满足的条件是　　　　时，；当满足的条件是　　　　时，．

			0	1	2	3
			0	2	0

三、解答题（在答题卡上作答，写出必要的解题步骤．题每小题6分，题每小题10分，24题12分，25题13分，共85分）．

16．解方程：．

17．一个瓶中装有一些幸运星，小王为了估计这个瓶中幸运星的颗数，他是这样做的：先从瓶中取出20颗幸运星做上记号，然后把这些幸运星放回瓶中，充分摇匀；再从瓶中取出30颗幸运星，发现有6颗幸运星带有记号．

请你帮小王估算出原来瓶中幸运星的颗数．

18．下面的统计图表是2006年佛山市某三间高中共4145人参加广州市模拟考、佛山市模拟考、全国统一高考的数学学科考试成绩情况：

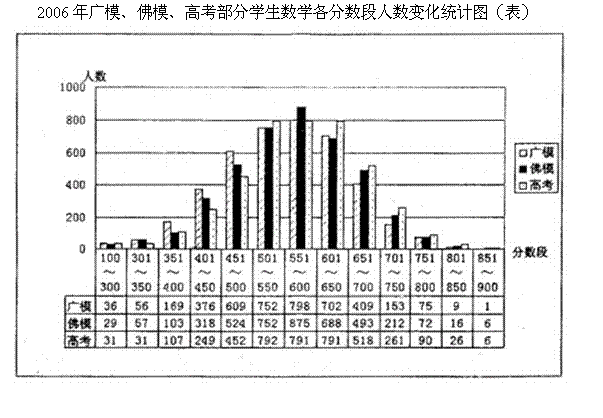
根据统计图表，请回答下列问题：

（1）在某个分段，广模与高考人数差距最大，相差人数是　　　　  ；

（2）在这个分数段中，高考人数比佛模人数增长了　　　　（填百分数，精确到期1%）；

（3）从图表中你还发现了什么信息（写出一条即可）？

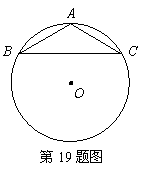19．如图，是的外接圆，且，求的半径．

20．上数学课时，老题提出了一个问题：“一个奇数的平方减1，结果是怎样的数？”请你解答这个问题．

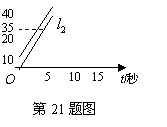
21．甲、乙两人进行百米赛跑，甲比乙跑得快．如果两人同时起跑，甲肯定赢．现在甲让乙先跑若干米．图中分别表示两人的路程（米）与时间（秒）的关系．

s/米

（1）哪条线表示甲的路程与时间的关系？

80

（2）甲让乙先跑了多少米？

60

（3）谁先到达终点？

22．佛山市的名片“一环”路全长约为99公里，其中：东线长36公里，西线长32公里，南线长15公里，北线长15.6公里（为计算方便，以上数据与实际稍有出入）

　　　 小明同学想根据以上信息估算“一环”路的环内面积，他把佛山“一环”路的形状理想化为一个四边形进行研究，他想到的图形有如下四种：

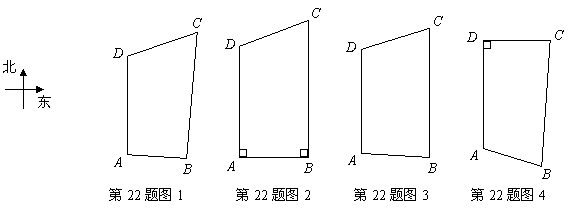
（1）如果让你来研究，你会选择哪个图形（注：图3中）？

请你利用选定的图形，把所给信息中的三个数据作为其中三边的长，计算出第四边的长，并比较它与实际长的误差是多少？

参考数据：，．

（2）假设边长的误差在0.5公里以内，就可以用所选择的图形近似计算环内面积．你选择的图形是否符合以上假设？若符合，请计算出环内面积．

23．如图，在中，是的中点，．

（1）求证：；

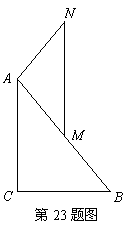（2）如果把条件“”改为“”，其它条件不变，那么不一定成立．如果再改变一个条件，就能使成立．

请你写出改变的条件并说明理由．

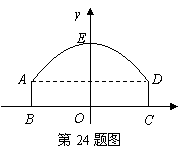
24．如图，隧道的截面由抛物线和矩形构成，矩形的长为，宽为，以所在的直线为轴，线段的中垂线为轴，建立平面直角坐标系，轴是抛物线的对称轴，顶点到坐标原点的距离为．

（1）求抛物线的解析式；

（2）一辆货运卡车高，宽2.4m，它能通过该隧道吗？

（3）如果该隧道内设双行道，为了安全起见，在隧道正中间设有0.4m的隔离带，则该辆货运卡车还能通过隧道吗？

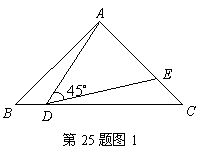25．在中，，

点在所在的直线上运动，作

（按逆时针方向）．

（1）如图1，若点在线段上运动，交于．

①求证：；

②当是等腰三角形时，求的长．

（2）①如图2，若点在的延长线上运动，的反向延长线与的延长线相交于点，是否存在点，使是等腰三角形？若存在，写出所有点的位置；若不存在，请简要说明理由；

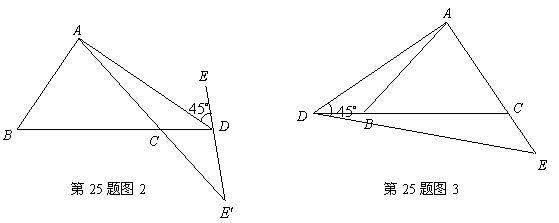②如图3，若点在的反向延长线上运动，是否存在点，使是等腰三角形？若存在，写出所有点的位置；若不存在，请简要说明理由．