中考数学规律探索问题试题汇编
一、选择题
1、(2007山东济宁)如图,是一个装饰物品连续旋转闪烁所成的三个图形,照此规律闪烁,下一个呈现出来的图形是( )。B
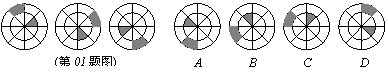 |
2、(2007江苏泰州)按右边![]() 方格中的规律,在下面4个符号中选择一个填入方格左上方的空格内( )A
方格中的规律,在下面4个符号中选择一个填入方格左上方的空格内( )A
3、(2007湖南湘潭)为庆祝“六![]() 一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:
一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:

按照上面的规律,摆![]() 个“金鱼”需用火柴棒的根数为( )A
个“金鱼”需用火柴棒的根数为( )A
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、(2007湖南株州)某种细胞开始有2个,1小时后分裂成4个并死去1个,2小时分裂成6个并死去1个,3小时后分裂成10个并死去1个,按此规律,5小时后细胞存活的个数是( )C
A. 31 B. 33 C. 35 D. 37
二、填空题
1、(2007辽宁沈阳)有一组数:1,2,5,10,17,26,……,请观察这组数的构成规律,用你发现的规律确定第8个数为 .50
1、(2007山东日照)把正整数1,2,3,4,5,……,按如下规律排列:
1
2,3,
4,5,6,7,
8,9,10,11,12,13,14,15,
 … … … …
… … … …
按此规律,可知第n行有 个正整数.2n-1
2、(2007重庆)将正整数按如图所示的规律排列下去。若用有序实数对(![]() ,
,![]() )表示第
)表示第![]() 排,从左到右第
排,从左到右第![]() 个数,如(4,3)表示实数9,则(7,2)表示的实数是
。23
个数,如(4,3)表示实数9,则(7,2)表示的实数是
。23
3、(2007福建晋江)试观察下列各式的规律,然后填空:
![]()
![]()
![]() ……
……
则![]() _______________。
_______________。![]() 。
。
4、(2007内蒙古赤峰)观察下列各式:
![]()
![]()
![]()
……
依此规律,第![]() 个等式(
个等式(![]() 为正整数)为
.
为正整数)为
.![]()
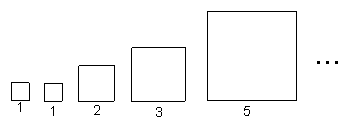
5、(2007浙江温州)意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,
其中从第三个数起,每一个数都等于它前面两上数的和。现以这组数中的各个数作为正方形的长度构造如下正方形:
| 序号 | ① | ② | ③ | ④ |
| 周长 | 6 | 10 | 16 | 26 |
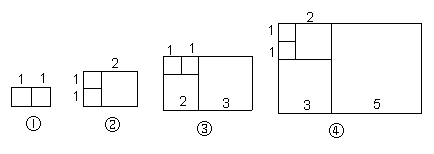 再分别依次从左到右取2个、3个、4个、5个,正方形拼成如下矩形并记为①、②、③、④.相应矩形的周长如下表所示:
再分别依次从左到右取2个、3个、4个、5个,正方形拼成如下矩形并记为①、②、③、④.相应矩形的周长如下表所示:
 若按此规律继续作矩形,则序号为⑩的矩形周长是_______。466
若按此规律继续作矩形,则序号为⑩的矩形周长是_______。466
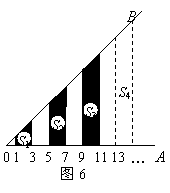
6、(2007福建福州)如图6,![]() ,过
,过![]() 上到点
上到点![]() 的距离分别为
的距离分别为
![]() 的点作
的点作![]() 的垂线与
的垂线与![]() 相交,得到并标出
相交,得到并标出
一组黑色梯形,它们的面积分别为![]() .
.
 观察图中的规律,求出第10个黑色梯形的面积
观察图中的规律,求出第10个黑色梯形的面积![]() .76
.76
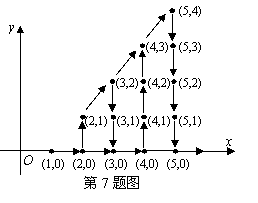
7、(2007四川德阳)如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“![]() ”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)
”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)![]() 根据这个规律探索可得,第
根据这个规律探索可得,第![]() 个点的坐标为____________.
个点的坐标为____________.![]()
8、(2007四川自贡)一个叫巴尔末的中学教师成功地从光谱数据![]() ,
,![]() ,
,![]() ,
,![]() ,…中得到巴尔末公式,从而打开了光谱奥秘的大门,请你按照这种规律,写出第n(n≥1)个数据是___________.
,…中得到巴尔末公式,从而打开了光谱奥秘的大门,请你按照这种规律,写出第n(n≥1)个数据是___________.
解:![]() 或
或![]()
9、(2007浙江临安)已知:
![]() , ……,若
, ……,若 ![]() 符合前面式子的规律, 则 a + b = ___ ____.109
符合前面式子的规律, 则 a + b = ___ ____.109
10、(2007湖南岳阳)观察下列等式: 第一行 3=4-1
第二行 5=9-4
第三行 7=16-9
第四行 9=25-16
… …
按照上述规律,第n行的等式为____________ (答案:2n+1=(n+1)2-n2)
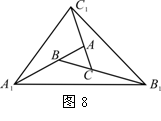 11、(2007四川资阳)如图8,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1;第二次操作,分别延长A1B1、B1C1、C1A1至点A2、B2、C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2、B2、C2,得到△A2B2C2,记其面积为S2;…;按此规律继续下去,可得到△A5B5C5,则其面积S5=_____________ . .
11、(2007四川资阳)如图8,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1;第二次操作,分别延长A1B1、B1C1、C1A1至点A2、B2、C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2、B2、C2,得到△A2B2C2,记其面积为S2;…;按此规律继续下去,可得到△A5B5C5,则其面积S5=_____________ . .
12、(2007浙江杭州)如图,![]() 是一块半径为1的半圆形纸板,在
是一块半径为1的半圆形纸板,在![]() 的左下端剪去一个半径为
的左下端剪去一个半径为![]() 的半圆后得到图形
的半圆后得到图形![]() ,然后依次剪去一个更小的半圆(其直径为前一个被剪掉半圆的半径)得图形
,然后依次剪去一个更小的半圆(其直径为前一个被剪掉半圆的半径)得图形![]() ,记纸板
,记纸板![]() 的面积为
的面积为![]() ,试计算求出
,试计算求出![]() ;
;![]() ;并猜想得到
;并猜想得到![]()
![]() 。
。
 |
解:![]()
 13、(2007广西河池非课改)填在下面三个田字格内的数有相同的规律,根据此规律,C = .108
13、(2007广西河池非课改)填在下面三个田字格内的数有相同的规律,根据此规律,C = .108
14、(2007广西河池课改)古希腊数学家把1,3,6,10,15,21,……,叫做三角形数,根据它的规律,则第100个三角形数与第98个三角形数的差为 .199
16、(2007山东威海)观察下列等式:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …
…
请你把发现的规律用字母表示出来:![]() .
.![]()
15、(2007山东烟台)观察下列各式:
![]() 请你将发现的规律用含自然数n(n≥1)的等式表示出来
.
请你将发现的规律用含自然数n(n≥1)的等式表示出来
.![]() =
=![]()
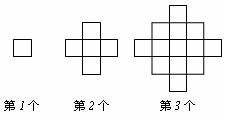
16、(2007湖北武汉)下列图案是由边长为单位长度的小正方形按一定的规律拼接而成。依此规律,第5个图案中小正方形的个数为_______________。41

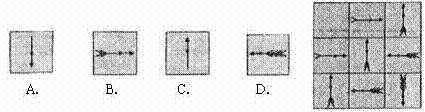
17、(2007湖北潜江)根据下列图形的排列规律,第2008个图形
是 (填序号即可). (①†;②‡;③‰;④ˆ.)
‡†‰ˆ‡‡†‰ˆˆ‡†‰ˆ…… 答:③
18、(2007广东韶关)按如下规律摆放三角形:
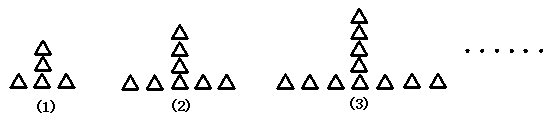

则第(4)堆三角形的个数为_____________;第(n)堆三角形的个数为_____________.14;3n+2
 19、(2007哈尔滨)柜台上放着一堆罐头,它们摆放的形状见右图:
19、(2007哈尔滨)柜台上放着一堆罐头,它们摆放的形状见右图:
第一层有![]() 听罐头,
听罐头,
第二层有![]() 听罐头,
听罐头,
第三层有![]() 听罐头,……
听罐头,……
根据这堆罐头排列的规律,第![]() (
(![]() 为正整数)层
为正整数)层
有
听罐头(用含![]() 的式子表示). 解:
的式子表示). 解:![]()
三、解答题
1、(2007四川内江)观察一列数2,4,8,16,32,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是 ;根据此规律,如果![]() (
(![]() 为正整数)表示这个数列的第
为正整数)表示这个数列的第![]() 项,那么
项,那么![]() ,
,![]() ;
;
(2)如果欲求![]() 的值,可令
的值,可令
![]() ……………………………………………………①
……………………………………………………①
将①式两边同乘以3,得 …………………………②
由②减去①式,得![]() .
.
(3)用由特殊到一般的方法知:若数列![]() ,从第二项开始每一项与前一项之比的常数为
,从第二项开始每一项与前一项之比的常数为![]() ,则
,则![]() (用含
(用含![]() 的代数式表示),如果这个常数
的代数式表示),如果这个常数![]() ,那么
,那么![]() (用含
(用含![]() 的代数式表示).
的代数式表示).
解:(1)2(1分) 218(1分) 2n(2分)
(2)3S=3+32+33+34+…+321(1分) S=![]() (1分)
(1分)
(3)a1qn-1(2分) ![]() (2分)
(2分)
 2、(2007贵州贵阳)如图12,平面内有公共端点的六条射线
2、(2007贵州贵阳)如图12,平面内有公共端点的六条射线![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,从射线
,从射线![]() 开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….
开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,….
(1)“17”在射线 上.(3分)
(2)请任意写出三条射线上数字的排列规律.(3分)
(3)“2007”在哪条射线上?(3分)
解:(1)“17”在射线![]() 上.
上.
(2)射线![]() 上数字的排列规律:
上数字的排列规律:![]()
射线![]() 上数字的排列规律:
上数字的排列规律:![]()
射线![]() 上数字的排列规律:
上数字的排列规律:![]()
射线![]() 上数字的排列规律:
上数字的排列规律:![]()
射线![]() 上数字的排列规律:
上数字的排列规律:![]()
射线![]() 上数字的排列规律:
上数字的排列规律:![]()
(3)在六条射线上的数字规律中,只有![]() 有整数解.解为
有整数解.解为![]()
“2007”在射线![]() 上.
上.
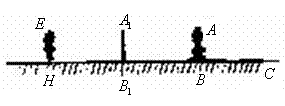
3、(2007浙江金华)学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为![]() 的小明
的小明![]() 的影子
的影子![]() 长是
长是![]() ,而小颖
,而小颖![]() 刚好在路灯灯泡的正下方
刚好在路灯灯泡的正下方![]() 点,并测得
点,并测得![]() .
.
(1)请在图中画出形成影子的光线,交确定路灯灯泡所在的位置![]() ;
;
(2)求路灯灯泡的垂直高度![]() ;
;
 (3)如果小明沿线段
(3)如果小明沿线段![]() 向小颖(点
向小颖(点![]() )走去,当小明走到
)走去,当小明走到![]() 中点
中点![]() 处时,求其影子
处时,求其影子![]() 的长;当小明继续走剩下路程的
的长;当小明继续走剩下路程的![]() 到
到![]() 处时,求其影子
处时,求其影子![]() 的长;当小明继续走剩下路程的
的长;当小明继续走剩下路程的![]() 到
到![]() 处,…按此规律继续走下去,当小明走剩下路程的
处,…按此规律继续走下去,当小明走剩下路程的![]() 到
到![]() 处时,其影子
处时,其影子![]() 的长为
m(直接用
的长为
m(直接用![]() 的代数式表示).
的代数式表示).
解:(1)
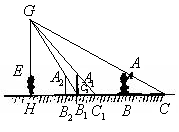

(2)由题意得:![]() ,
,
![]() ,
,![]() ,
,![]() (m).
(m).
(3)![]() ,
,![]() ,
,
设![]() 长为
长为![]() ,则
,则![]() ,解得:
,解得:![]() (m),即
(m),即![]() (m).
(m).
同理![]() ,解得
,解得![]() (m),
(m),![]() .
.
4、(2007四川乐山)如图(15),在直角坐标系中,已知点![]() 的坐标为
的坐标为![]() ,将线段
,将线段![]() 按逆时针方向旋转
按逆时针方向旋转![]() ,再将其长度伸长为
,再将其长度伸长为![]() 的2倍,得到线段
的2倍,得到线段![]() ;又将线段
;又将线段![]() 按逆时针方向旋转
按逆时针方向旋转![]() ,长度伸长为
,长度伸长为![]() 的2倍,得到线段
的2倍,得到线段![]() ;如此下去,得到线段
;如此下去,得到线段![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() 为正整数)
为正整数)
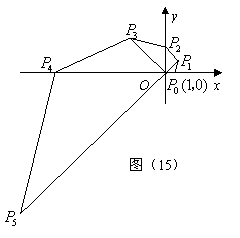 (1)求点
(1)求点![]() 的坐标;
的坐标;
(2)求![]() 的面积;
的面积;
(3)我们规定:把点![]() (
(![]() )
)
的横坐标![]() 、纵坐标
、纵坐标![]() 都取绝对值后得到的新坐标
都取绝对值后得到的新坐标
![]() 称之为点
称之为点![]() 的“绝对坐标”.
的“绝对坐标”.
根据图中点![]() 的分布规律,请你猜想点
的分布规律,请你猜想点![]() 的“绝对坐标”,并写出来.
的“绝对坐标”,并写出来.
解:(1)根据旋转规律,点![]() 落在
落在![]() 轴的负半轴,而点
轴的负半轴,而点![]() 到坐标原点的距离始终等于前一个点到原点距离的
到坐标原点的距离始终等于前一个点到原点距离的![]() 倍,故其坐标为
倍,故其坐标为![]() ,即
,即![]() .
.
(2)由已知可得,
![]() ,
,
设![]() ,则
,则![]() ,
,![]()
又![]()
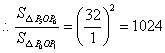 ,
,![]()
(3)由题意知,![]() 旋转
旋转![]() 次之后回到
次之后回到![]() 轴正半轴,在这
轴正半轴,在这![]() 次中,点
次中,点![]() 分别落在坐标象限的平分线上或
分别落在坐标象限的平分线上或![]() 轴或
轴或![]() 轴上,但各点绝对坐标的横、纵坐标均为非负数,因此,点
轴上,但各点绝对坐标的横、纵坐标均为非负数,因此,点![]() 的坐标可分三类情况:令旋转次数为
的坐标可分三类情况:令旋转次数为![]()
①当![]() 或
或![]() 时(其中
时(其中![]() 为自然数),点
为自然数),点![]() 落在
落在![]() 轴上,
轴上,
此时,点![]() 的绝对坐标为
的绝对坐标为![]() ;
;
②当![]() 或
或![]() 或
或![]() 或
或![]() 时(其中
时(其中![]() 为自然数),点
为自然数),点![]() 落在各象限的平分线上,此时,点
落在各象限的平分线上,此时,点![]() 的绝对坐标为
的绝对坐标为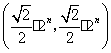 ,即
,即![]()
③当![]() 或
或![]() 时(其中
时(其中![]() 为自然数),点
为自然数),点![]() 落在
落在![]() 轴上,
轴上,
此时,点![]() 的绝对坐标为
的绝对坐标为![]() .
.
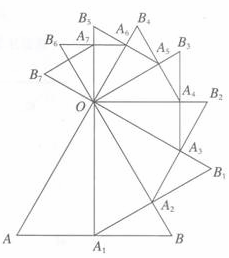
5、(2007广东省)已知等边△OAB的边长为a,以AB边上的高OA1为边,按逆时针方向作等边△OA1B1,A1B1与OB相交于点A2。
(1)求线段OA2的长;
(2)若再以OA2为边按逆时针方向作等边△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,┉,△OAnBn,(如图),求△OA6B6,的周长。