中考数学解直角三角形复习测试3

　　　　　 解直角三角函数

一、知识点回顾

1、锐角∠A的三角函数（按右图Rt△ABC填空）　　

∠A的正弦：sinA =　　　　  ,　

∠A的余弦：cosA =　　　　  ,

∠A的正切：tanA = 　　　　　,　

 ∠A的余切：cotA = 　　　　　

2、锐角三角函数值，都是　　 实数（正、负或者0）；

3、正弦、余弦值的大小范围：　　　　 　　＜sin A＜　　； 　　＜cos A＜　　

4、tan A•cotA =　　  ；　　　 tan B•cotB =　　  ；

5、sinA = cos（90°- 　　 ）；  cosA = sin（　　- 　 ）

tanA =cot（　　　　 ）； 　 cotA =　　　　　  　

6、填表

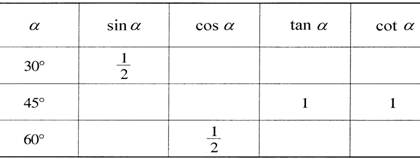
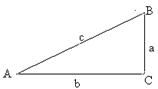7、在Rt△ABC中，∠C＝90，AB＝c,BC＝a，AC＝b,

　1）、三边关系（勾股定理）：　　　　　　　　　 

　　2）、锐角间的关系：∠　 +∠　　 = 90°

　  3）、边角间的关系：sinA =　　　　  ； sinB =　　　　  ；

cosA =　　　　  ；　cosB=　　　　  ；　　　　　　　　　　 

tanA =　　　　  ；　tanB =　　　　  ；

cotA = 　　　　　 ；cotB = 　　　　 

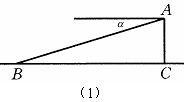
8、图中角可以看作是点A的　　　角

也可看作是点B的　　　　角；

9、（1）坡度（或坡比）是坡面的　　高度（h）和　 长度（l）的比。

记作i,即i =　　；

（2）坡角——坡面与水平面的夹角。记作α，有i＝=tanα

（3）坡度与坡角的关系：坡度越大，坡角α就越　　　，坡面就越 　　

二、巩固练习

（1）、三角函数的定义及性质

1、在△中,,则cos的值为　　 　 

2、在Rt⊿ABC中，∠C＝90°，BC＝10，AC＝4，则；

3、Rt△中,若,则tan

4、在△ABC中，∠C＝90°，，则　　　　   

5、已知Rt△中,若cos,则

6、Rt△中,，那么

7、已知，且为锐角，则的取值范围是　　　　　 ；

8、已知：∠是锐角，，则的度数是 　　　　　　　　　　　　　　　　 

9、当角度在到之间变化时，函数值随着角度的增大反而减小的三角函是　 （　　）

A．正弦和正切 　B．余弦和余切 　 C．正弦和余切 　 D．余弦和正切

10、当锐角A的时，∠A的值为（　　）　　　　　　　　　　　　　　　　 

A　小于　　 B  小于　　C 大于　　D 大于

11、在⊿ABC中，若各边的长度同时都扩大2倍，则锐角A的正弦址与余弦值的情况（　　）

A　都扩大2倍　  B 都缩小2倍　　C 都不变　　 D　　 不确定

12、已知为锐角，若，＝　　　；若，则；

13、在△中,sin, 则cos等于(　　)

A、　　　　　 B、　　　　　 C、　　　　  D、

（2）、特殊角的三角函数值

1、在Rt△ABC中，已知∠C＝90⁰，∠A=45⁰则=　　　　 

2、已知：是锐角，，tan=______；

3、已知∠A是锐角，且；

4、在平面直角坐标系内P点的坐标（，），则P点关于轴对称点P^／的坐标为  （　　）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

A．　 　　 B．　 　　C．　 　　D．　

5、下列不等式成立的是（　  ）

A．　　 　　B．

C．　　 　　D．

6、若，则锐角的度数为（　　　）

A．20⁰　　　　B．30⁰　　　　 C．40⁰　　　　 D．50⁰　　

7、计算

（1）；

（2）

(3)　　  (4)

（3）、解直角三角形

1、在△中,如果，求的四个三角函数值.

解：（1）∵ a ²+b ²＝c ²

∴ c =　　　　　　　　　  　　　　　　　　　　　　　　

　　　　　　 ∴sinA =　　　　　　  cosA =　　　　 

∴tanA =　　　　   cotA = 　　　　　　 

2、在Rt△ABC中，∠C＝90°，由下列条件解直角三角形：

（1）已知a＝4，b＝2，则c=　　　　　 ；

（2）已知a＝10，c＝10，则∠B=　　　　　  ；

（3）已知c＝20，∠A＝60°，则a=　　　　　　  ；　　

（4）已知b＝35，∠A＝45°，则a=　　　　　　  ；

3、若∠A = ，，则；

4、在下列图中填写各直角三角形中字母的值．

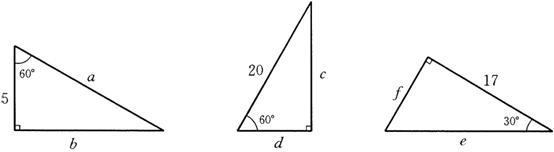
7、设Rt△ABC中，∠C＝90，∠A、∠B、∠C的对边分别为a、b、c，根据下列所给条件求∠B的四个三角函数值.

（1）a =3,b =4;　　　　　　　　　  　（2）a =6,c =10.

8、在Rt△ABC中，∠C＝90，BC：AC＝3：4，求∠A的四个三角函数值.

9、△中,已知，求的长

（4）、实例分析

1、斜坡的坡度是，则坡角

2、一个斜坡的坡度为︰，那么坡角的余切值为　　　　  ；

3、一个物体点出发，在坡度为的斜坡上直线向上运动到，当m时，物体升高　　　　　　　 （　　）

A　m　　　  B　 m　　　  C　m　　D 不同于以上的答案

4、某水库大坝的横断面是梯形，坝内斜坡的坡度，坝外斜坡的坡度，则两个坡角的和为 （　　）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

A　　　　 B　　　　 C　　　　 D　

5、电视塔高为m，一个人站在地面，离塔底一定的距离处望塔顶，测得仰角为，若某人的身高忽略不计时，m.

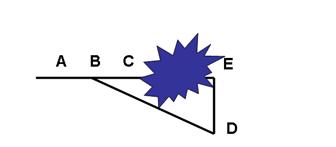
6、如图沿AC方向修隧道,为了加快施工进度,要在小山的另一边同时进行.已知∠ABD=150⁰,BD=520m,∠B=600,那么开挖点E到D的距离DE=____m时,才能使A,C,E成一直线.

7、一船向东航行，上午8时到达处，看到有一灯塔在它的南偏东，距离为72海里的处，上午10时到达处，看到灯塔在它的正南方向，则这艘船航行的速度为（　 ）

A 海里/小时　　　　　　　 B 海里/小时　　

C 海里/小时　　　　　　　 D 海里/小时　

8、如图，河对岸有铁塔AB，在C处测得塔顶A的仰角为30°，向塔前进14米到达D，在D处测得A的仰角为45°，求铁塔AB的高。

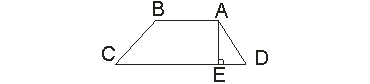
9、如图，一铁路路基横断面为等腰梯形，斜坡的坡度为，路基高为m，底宽m，求路基顶的宽

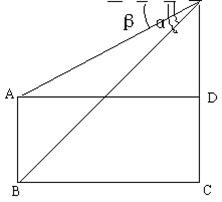
10、如图，已知两座高度相等的建筑物AB、CD的水平距离BC＝60米，在建筑物CD上有一铁塔PD，在塔顶P处观察建筑物的底部B和顶部A，分别测行俯角，求建筑物AB的高。（计算过程和结果一律不取近似值）

11、如图，A城气象台测得台风中心在A城的正西方300千米处，以每小时10千米的速度向北偏东60º的BF方向移动，距台风中心200千米的范围内是受这次台风影响的区域。

（1） 问A城是否会受到这次台风的影响？为什么？

（2） 若A城受到这次台风的影响，那么A城遭受这次台风影响的时间有多长？

解直角三角形总复习答案

二、巩固练习

（1）三角函数的定义和性质

1、　　 2、 、 　　 3、2　　　　 4、　　　　

5、10　　 6、　　　 7、　　　 8、54　　

9、B　　 10、 A　　　 11、C　　　 12、　　 13、B　　

（2）特殊角的三角函数值

1、　　2、1　　　3、　　 4、A　　5、D　  6、A

7、（1）1、　　  （2）或

　（3）　　　　  (4)　

（3）解直角三角形

1、　　 　　　 

2、（1）　　（2）10　　（3）　　 （4）35

3、 5 、　　 4、　　 5、　

6、 　 　　　

7、（1）　　　　 

（2）　　　　 

8、解：设BC=3k，AC=k

　

9、解：过A作ADBC，垂足为D。

　

　

　

　

　

（4）实例分析

1、　　2、　　3、C　  4、C　　 5、

6、　　　 7、B

8、解：设铁塔AB高x米

　

　

　 在中

　

即

解得：x=m

答：铁塔AB高m。

9、解：过B作BFCD，垂足为F

　

在等腰梯形ABCD中

AD=BC　

AE=3m

DE=4.5m

AD=BC，,

BCFADE

CF=DE=4.5m

EF=3m

BF//CD

四边形ABFE为平行四边形

AB=EF=3m

10、

解：

在RTBPC中

在矩形ABCD中

AD=BC=60m

在RTAPD中

AD=60m,

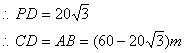
答：AB高米。

11、（1）过A作ACBF，垂足为C

在RTABC中

AB=300km

(2)

答：A城遭遇这次台风影响10个小时。