《解直角三角形》提高测试
一 选择题（本题15分，每小题3分）：
1．下列相等、不等关系中，成立的是…………………………………………………（ ）
（A）sin60°＞cos30°，tan30°＜cot60°
（B）sin60°＞cos30°，tan30°＞cot60°
（C）sin60°－cos30°＝tan30°－cot60°＝0
（D）sin260°＋cos230°＝1
２．
的值等于……………………………………………………（ ）
（A）－1－
（B）－
（C）
（D）1＋
３．当锐角
≤45°时，角的正切和余切值的大小关系应是……………………（ ）
（A）tan≤cot （B）tan≥cot （C）tan＝cot （D）不确定
４．在直角三角形中，各边的长度都扩大3倍，则锐角A的四个三角形函数的值（ ）
（A）也扩大3倍
（B）缩小为原来的
（C）都不变 （D）有的扩大，有的缩小
５．在三角形ABC中，C为直角，sinA＝
，则tanB 的值为…………………（ ）
（A）
（B）
（C）
（D）
答案：
１．Ｃ；２．Ｄ；３．Ａ；４．Ｃ；５．Ｄ．
二 填空题（本题20分，每小题4分）：
１．已知tan＝
，是锐角，则sin＝ ；
２．等于1的三角函数有 ；
３．
＝ ；
４．cos2（50°＋）＋cos2（40°－）－tan（30°－）tan（60°＋）＝ ；
５．a3tan45°＋a2btan260°＋3ab2cot260°＝ ．
答案：
１．
；
２．sin90°，cos0°，tan45°，cot45°；
３．tan50°－tan40°；
４．0；
５．a（a＋b）2.
三 解下列直角三角形（本题32分，第小题8分）：
在直角三角形ABC中，∠C＝90°：△
１．已知：b＝
，
；
解：S△ABC＝
，
a＝10．
∴ tanA＝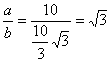
．
∴ ∠A＝60°，∠B＝30°，
∴ c＝2b＝2
＝
．
２．已知：∠B＝45°，a＋b＝10；
解：依题意，∠A＝∠B＝45°，
所以
a＝b＝5；
由 sinA＝sin45°＝
得
∴
，
c＝
．
３．已知：c边上的高h＝4，b＝5；
解：依题意，有
∠A≈53°8′，B≈36°52′；
另一方面，有
a＝b tan A＝5×
＝5×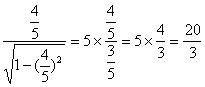
∴ sinA＝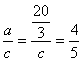
，
c＝
４．已知：B＝30°，CD为AB边上的高，且CD＝4．
解：如图，CD＝4，在Rt△CDB 中，有
BC＝a＝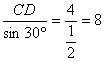
，A＝60°；
另一方面，有
∴ 
c＝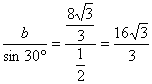
．
四 （本题16分）
在四边形ABCD中，AC恰好平分∠A，AB＝21，AD＝9，BC＝CD＝10，试求AC的长．
略解：利用角平分线的性质，构造直角三角形：
作CE⊥AB于E，CF⊥AD于F，
易证CEB≌△CFD，
则有EB＝FD；
又可证△CEA≌△CFA，
于是由 AE＝AF 可得
21－EB＝9＋FD，
∴ EB＝FD＝6；
在Rt△AFC中，有
AC＝
＝
.
五 （本题17分）
一艘船向正东方先航行，上午10点在灯塔的西南方向k海里处，到下午2点时航行到灯塔的东偏南60°的方向，画出船的航行方位图，并求出船的航行速度．
解：如图，依题意，灯塔位于P点，船丛A 点向东航行，12点到达C点，
且有 PB⊥AC，A＝45°，∠BPC＝30°；
于是，在△ABP中，有
AB＝PB＝AP cos45°
＝k 
.
在△PBC中，又有
BC＝PB tan30°
＝
k，
所以
AC＝
.
可知船的航行速度为
．
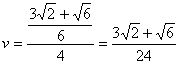