中考数学解直角三角形练习-中考数学试题、初中数学中考试卷、模拟题、复习资料-初中数学试卷-试卷下载

中考数学解直角三角形练习

第一课时(锐角三角函数)

课标要求

1、　通过实例认识直角三角形的边角关系，即锐角三角函数（sinA、cosA、tanA 、cotA）

2、　熟知30⁰、45⁰、60⁰角的三角函数值

3、　会用计算器求锐角的三角函数值，以及由已知的三角函数值求相应的锐角。

4、　通过特殊角三角函数值，知道互余两角的三角函数的关系。

5、　了解同角三角函数的平方关系。sin²α+cos²α=1，倒数关系tanα·cotα=1.

6、　熟知直角三角形中，30⁰角的性质。

中招考点

1、　锐角三角函数的概念，锐角三角函数的性质。

2、　30⁰、45⁰、60⁰角的三角函数值及计算代数式的值。

3、　运用计算器求的三角函数值或由锐角三角函数值求角度。

典型例题

A　　　　　　C

图19-1

[例题1]　选择题（四选一）

1、如图19-1，在Rt△ABC中，CD是斜边AB上的高，则下列线段比中不等于sinA的是（　　）

A. 　　 B. 　　C.　 D.

分析：sinA=, sinA=sinÐBCD= ;sinA= ,从而判断D不正确。故应选D.。

2、在Rt△ABC中，ÐC＝90⁰，ÐA＝ÐB，则cosA的值是（　　）

A.　　　B.　　 C.　 D.1

分析：先求出ÐA的度数，因为ÐC＝90⁰，ÐA＝ÐB，故ÐA＝ÐB＝45⁰，再由特殊角的三角函数值可得：cosA=cos45⁰= 故选B.。

3、在△ABC中，ÐC＝90⁰，sinA= ,则cosB的值为（　　）

A.　　　B.　　 C.　 D.

分析：方法一：因为sinA=,故锐角A＝60⁰。因为ÐC＝90⁰，所以ÐB＝30⁰. cosB= .故选C.

方法二：因为 ÐC＝90⁰，故 ÐA与 ÐB互余.所以cosB=sin A＝.故选C..

4、如图19-2，在△ABC中，ÐC＝90⁰，sinA=.则BC：AC等于（　　　）

A　　　　　　　C

图19-2

A.　3：4　　　B.　4：3　　 C.3：5　　 D.4：5

分析：因为ÐC＝90⁰，sinA＝　,又sinA= .所以＝, 不妨设BC＝3k,AB=5k,由勾股定理可得AC＝＝4k,所以BC：AC＝3k:4k=3:4故选A.。

注意：由＝，不能认为BC＝3，AB＝5。

　　　　A　　　　　　D

D^/　　　　B　　　　C

图19-3

5、如图19-3，已知正方形ABCD的边长为2，如果将线段BD绕着点B旋转后，点D落在CB的延长线上的D^/处，那么tanÐBAD^/等于（　　）

A.　1 　 B.　　C.　　D.2

分析：根据勾股定理得

BD＝==2

又BD^/＝BD＝2，AB＝2，

在Rt△ABD^/中，tanÐBAD^/= 　

　故选B.。

6、在∆ABC中，若｜sinA- +(-cosB)²=0, ∠A.∠B都是锐角，则∠C的度数是（　　　）

A.　75⁰　　　B.　90⁰　　 C.105⁰　　D.120⁰

分析：　由｜sinA- +(-cosB)²=0可得，

sinA-=0　　-cosB=0 即 sinA=　　=cosB　 ,又∠A、∠B都是锐角，∴∠A＝45⁰，∠B＝30⁰.由三角形内角和知，∠C＝180⁰-∠A-∠B＝105⁰.故选C.

评注：解决此题的关键是利用利用非负数性质，求sinA、cosB的值，得出∠A、∠B的度数。

[例2] 填空题：

1、计算tan60⁰sin60⁰-cot30⁰tan45⁰=_________

分析　熟记30⁰、45⁰、60⁰这些特殊角的三角函数值是解决本题的关键。

　原式＝

2、在∆ABC中，ÐC=90⁰.若tanA= 　则sinB的值等于_________

分析　依据条件tanA= ,可求出cotB=cot(90⁰-A )=tanA= ,再由cotB= 　　　　　及sin²B+cos²B=1得　cotB＝　可求出sinB= 　

3、在∆ABC中，ÐC=90⁰，若∠B＝2∠A，则cotB的值为_______.

分析　因为∠A+∠B＝90⁰，且∠B＝2∠A，故∠B＝60⁰.　所以　cotB=cot60⁰=　

4、　若α为锐角，且cos(90⁰-α)＝，则α的度数是＿＿＿＿

分析把90⁰-α当作一个整体，由特殊角的三角函数值，易得90⁰-α=60⁰,所以α＝30⁰.

5、　已知0⁰＜α＜40⁰，且sin(α+10⁰)=cos(50⁰+α)，则α＝＿＿＿＿＿＿＿＿

分析　根据互余两角的三角函数关系，因为0⁰＜α＜40⁰，所以10⁰＜α+10⁰＜50⁰，50⁰＜50⁰+α＜90⁰，从而有（α+10⁰）+（50⁰+α）＝90⁰　∴α＝15⁰.

6、　用计算器计算：sin56⁰50^/+cos39⁰30^/-tan46⁰10^/=_______

分析　会用计算器求任意一个锐角的三角函数值，然后进行计算。原式＝0.5671.

7、已知方程4x²-2(m+1)x+m=0的两根恰为一个直角三角形两锐角的余弦，则m=______

分析　设这个直角三角形的两个锐角分别为α、β，且α+β＝90⁰。cosβ=sinα.由一元二次方程根与系数的关系得：cosα+cosβ=，cosαcosβ=

∴ cosα+sinα= . cosαsinα=　

又因∵sin²α+cos²α=1，(sinα+cosα)²-2sinαcosα=1.

∴ .∴(m+1)²-2m=4 ∴m=±

∵α、β都是锐角，

∴　cosα＞0，sinα＞0

∴m=-应舍去.故m=.

[例3]　在 ∆ABC中，AB＝AC.　且AB＝2BC.　求ÐB的四个三角函数值。

分析　根据锐角的三角函数的定义知，锐角三角函数值是锐角所在的直角三角形相应边的比值。因此必须把∠B放入直角三角形中，由题可知，∆ABC中没有说是直角三角形，所以要想法构造出直角三角形。

B　　 D　　 C

图19-4

解：　如图19-4，过点A作AD⊥BC，垂足为D。

∵AB＝AC

∴BD＝DC＝BC.

又AB＝2BC

∴AB＝4BD

在Rt∆ABD中，AD＝

∴　sinB=

cosB=

tanB=

cotB=

［例4］计算

分析：　本题主要是考察特殊角的三角函数值和分母有理化知识

解：　原式＝.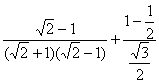

［例5］　要求tan30⁰的值.可构造如图19-5所示的直角三角形进行计算，作Rt∆ABC，使ÐC=90⁰，斜边AB＝2，直角边AC＝1，那么BC＝　∠ABC＝30⁰，所以　tan30⁰=

在此图的基础上，通过添加适当的辅助线，可求出tan15⁰的值。请你就此图添加辅助线，并求出tan15⁰的值。

分析：只需找出一个15⁰的角，并放入一个可求出各边长的直角三角形中。

解：延长CB至D，使BD＝AB。连结AD，如图19-6

A　　　　　　　　　　　　　　　　　A

2　　　　　1

　　　　　　　　　　　　　2　　　　　　1

30⁰

B　　　　　　　　C　　D　　　　　　　B　　　　　　　C

　图19-5　　　　　　　　　　　图19-6

则BD＝2，ÐD＝15⁰

所以　DC＝DB+BC＝2+

在Rt∆ADC中tanD=tan15⁰=　　

评注：　利用含30⁰角的直角三角形巧妙地构造出含15⁰角的直角三角形，从而求出15⁰角的三角函数值。利用此图还可以求出75⁰的各三角函数值。

强化训练

一、填空题：

⒈　在∆ABC中，若AC＝。BC＝　AB＝3，则cosA=____________.

⒉　在Rt∆ABC中，∠C＝90⁰.　tanA=. AC＝4.　则 BC=__________。

⒊　已知sinα＝　α为锐角。则tan =______________

⒋ 　在∆ABC中，若｜sinβ-+(cosA- )²=0. 　则∠C的度数为＿＿＿＿＿＿＿

⒌　若∠α的余角为38⁰，则∠α＝＿＿＿度，sinα=________(结果保留4个有效数字)

⒍　在∆ABC中，∠C＝90⁰.　AC＝AB. 则sinA=___________tanB=___________.

⒎　已知+1是方程x²-(3tanθ)x+ =0的一个根，θ为锐角三角形的一个内角，那么θ＝＿＿＿

⒏　若α+β＝90⁰.　则tanα·tanβ-tan =___________

⒐ 　在Rt∆ABC中，∠C＝90⁰.AB＝c.　BC＝a. 且a、c满足3a²-4ac+c²=0.　则sinA=________

⒑ 　在菱形ABCD中，∠A＝60⁰.　对角线AC＝6cm. 　则菱形的面积为＿＿＿＿＿＿＿＿　

二、选择题（四选一）

⒈　在∆ABC中，∠C＝90^0.tanA=1，那么cotB等于（　　　）

A.　　　B.　　　C.1　　　D.　

⒉　已知α为锐角，且tan(90⁰-α)= 　，则α的度数为（　　）

A.30⁰　　　B. 45⁰　　C.60⁰　　D.75⁰

⒊ 在 Rt∆ABC中，∠C＝90⁰.AC=12，cosA=　　 ,则 tanA等于(　　　　　　 ).

A.　　　B.　　C.　　　D.

⒋ 下列等式不成立的是(　　　　 )。

A. tanA·cotB=1　　B.tanA=　 C.tanA=　　 D.sin²60⁰+sin²30⁰=1　

⒌ 下列各式计算错误的是(　　　　)

A. cos30⁰+sin60⁰cos60+sin45⁰=　　　B.

C. sin30⁰tan42⁰tan48⁰+tan50⁰tan40⁰cos60⁰=1　 D.

⒍ 在∆ABC中，sinB=cos(90⁰-C)= 那么∆ABC是(　　　　 )

A.等腰三角形　　B.等边三角形　　　C.直角三角形　D.等腰直角三角形

⒎ 已知α为锐角，下列结论：⑴ sinα+cosα=1 ⑵ 如果α＞45⁰，那么sinα＞cosα. ⑶　如果cosα＞,那么α＜60⁰　 ⑷ =1-sinα,正确的有(　 )

A.1个　　B.2个　　　C.3个　　　D.4个

⒏　菱形ABCD的对角线AC=6，BD=8，∠ABD=α，则下列结论正确的是(　　 )

A.sinα=　　　B.cosα=　 C.tanα=　　D.cotα=

⒐　已知点P(3，sin60⁰)，则点P关于原点对称的点的坐标是(　　 )

A.(3，-)　　B.(-3，- )　　C.(3，sin60⁰)　　D.(-3,- )

⒑　已知α、β都是锐角，且α+β=90⁰，则关于x的一元二次方程

x²·cotα-2x+cotβ=0的根的情况是(　　 )。

A.有两个不等实数根B.有两个相等实数根　C.无实数根D.根的情况由α、β值确定。　

三、解答下列各题：

⒈ 计算：sin30⁰+cos60⁰-cot²45⁰-tan60⁰tan30⁰

⒉ 当x=sin45⁰+tan60⁰时。先将代数式 ÷(1+)化简后再求值。

B　　　　　　　　　　 C

图19-7

⒊ 在Rt∆ABC中，∠C＝90⁰. a-b＝2. tanA= ,求a、b、c的值。

⒋ 如图 19-7，已知∆ABC中，∠BAC＝90⁰.AB=AC. BD是AC边上的中线. 求cot∠DBC的值.

⒌　在∆ABC中，已知BC=1+　∠B=60⁰　 ∠C＝45⁰.求AB的长.

B　　　　　 P　　　　C

图19-8

⒍ 身高相同的甲、乙、丙三人放风筝，各人放出的线分别为300m、250m、200m，线与平面所成的角分别为30⁰、45⁰、60⁰(假定风筝线是拉直的)。问三人中谁放的风筝最高？

⒎ ∆ABC中，∠C＝90⁰，BC=8cm，sinB=，一只蜜蜂从点B开始沿BC向点C以2cm/s的速度移动。另一只蜜蜂从点C开始沿CA边向点A以1cm/s的速度移动。如果两只蜜蜂分别从B、C点同时出发各自运动到P、Q，如图19-8，第几秒钟时PQ∥AB？

第二课时(勾股定理、解直角三角形及有关知识解决实际问题)

课标要求

1、　熟悉勾股定理的探索过程，会用勾股定理解决简单的实际问题。

2、　运用三角函数解决与直角三角形有关的简单的实际问题。

3、　能综合运用直角三角形的勾股定理与边角关系解决简单的实际问题。

中招考点

1、　用勾股定理解决实际问题。

2、　直角三角形的基本解法(运用三角函数、勾股定理)。

3、　运用解直角三角形知识解决与生活、生产相关联的应用题。

典型例题

　　 A^/

B^/　　B　　　C

图19-9

［例1］如图19-9，在垂直于地面的墙上2m的点A斜放一个长2.5m的梯子，由于不小心梯子在墙上下滑0.5m，求梯子在地面上滑出的距离BB^/的长度。

分析： BB^/的长度应等于B^/C的长度减去BC的长度。因为在Rt∆ABC中，已知斜边AB和直角边AC的长，由勾股定理可求得BC的长，又由AA^/=0.5m，A^/B^/=AB，再次运用勾股定理可求出B^/C的长。

解：因为∠ACB=90⁰，AB=2.5m，AC=2m ，所以BC==1.5(m)

所以 A^/C=2-0.5=1.5(m)，A^/B^/=AB=2.5(m)

∴ B^/C= = 2(m)

∴ B^/B= B^/C-BC=2-1.5=0.5(m).

评注: 本题在理解题意的基础上，抓着梯子的长度不变，两次使用勾股定理，使问题得到解决。

［例2］ 如图19-10，已知在∆ABC中，∠ACB＝90⁰.AB=5cm，BC=3cm. CD⊥AB于D，求CD的长。

分析：先运用勾股定理求AC，再根据S_∆ABC=AB·CD=AC·BD，求出CD之长。

　　　　　　　　　　　　　　　B　　　D　　　　　　　 A

图19-10

解：因为∆ABC是直角三角形，AB=5 ，BC=3

由勾股定理有AC²=AB²-BC²

∴ AC==4

又S_∆ABC=AB·CD=BC·AC得

CD=(cm).

所以CD的长是 cm。

评注: 已知直角三角形任意两边长或两边关系及第三边的长，就可以求出三角形的未知边长，并可运用面积关系式求出斜边上的高(即弦高公式：两直角边的积等于弦与弦上高的积)。

［例3］在一棵树的10m高处有两只猴子，其中一只爬下树走向离树20m池塘，而另一只爬到树顶后直扑池塘。如果两只猴子经过的距离相等，问这一棵树有多高？

［分析］根据题意画出图形。在直角三角形中运用勾股定理求解。

C　　　　 20

图19-11

解：如图19-11，D为树顶，AB=10m，C为池塘，AC=20m。

设BD的长为x　m，则树高为(x+10) m.

因为 AC+AB=DB+DC

所以 DC= AC+AB-DB=20+10-x=30-x

在∆ACD中，∠A＝90⁰。所以AC²+AD²=DC²

故20²+(x+10)²=(30-x)²^。解得 x=5

所以 x+10=15. 即这一棵树的高为15m.

评注: 把实际问题变成几何问题，先画出符合题意的图形，设出某线段的长度，列出方程(组)来求解。

c　　　　　　 a

A　　　 b　　　　　　 C

图19-12

［例4］如图19-12所示，在∆ABC中，∠C＝90⁰，a=3，c=6，解这个三角形。

解： b²=c²-a²=(6)-(3)=81

∴ b=9

又因为sinA=　　所以∠A＝30⁰.

又因为∠A+∠B＝90⁰. 所以∠B＝60⁰.

∴　 b=9.　　 ∠A＝30⁰ .　　 ∠B＝60⁰.

评注: ⑴ 弄清直角三角形的边角关系是解直角三角形的关键。⑵在应用边角关系求未知边时，应尽是使用已知量，要避免使用中间求出的量，以便减少误差。⑶ 已知两边解直角三角形的思路：①已知两直角边a、b，直角三角形解法为 c=,由tanA=得∠A，∠B=90⁰-∠A。　　　②已知一直角边a和斜边c，直角三角形解法为 b=,由sinA=得∠A，∠B=90⁰- ∠A。

⑷ 已知一边和一锐角解直角三角形的思路：① 已知一条直角边a和一个锐角A，直角三角形的解法是：∠B=90⁰-∠A，c=　b=acotA(或b=)　② 已知斜边c和一个锐角B，直角三角形的解法是：已∠A=90⁰- ∠B，b=csinB, a=ccosB(或a= )。⑸ 要特别注意：凡是“解直角三角形 ”的题目，除题目中的已知元素，须把所有的未知元素全部求出来。

［例5］ 某市在“旧城改造”中计划在市内一块如图19-13所示的△ABC空地上种植草皮以美化环境。已知∠B=30⁰，∠C=45⁰，AB=20米，且知道这种草皮每平方米售价a元，请你算一算购买这种草皮共需要多少钱？

20米

　　　 30⁰　　　　　　　 45⁰

B　　　　　　　 D　　　　　 C

图19-13

分析： 要求草皮的费用，关键是求S_△ABC.故过点A作AD⊥BC于D，构造直角三角形分别求出AD、BD、CD即可。

解：作 AD⊥BC于D，在Rt△ABD中，∠B=30⁰

∴AD=AB=10m

∴BD= m

在Rt△ADC中，cotC=　DC=AD·cot45⁰=10m.

∴S_△ABC=(BD+CD)·AD=(10+10)×10=50(+1)(m²)

∵每平方米售价为a元，

∴共需要50(+1)a元

评注:采用“分割法”来构造直角三角形是解决问题的关键，但要特别注意，不要破坏题目中的已知条件。(即不能从B、C两点作高)。

［例6］ 某山区计划修建一条通过小山的公路，经测量，如图19-14，从山底B到山顶A的坡角是30⁰，斜坡AB长为100米，根据地形，要求修好的公路路面BD的坡比=1：5，为了减少工程量，若AD≤20米，则直接开挖修建公路；若AD＞20米，就要重新设计，问这段公路是否需要重新设计？

　　　　　　　　　 i=1: 5

B　　　　　　　　　　　　　 C

图19-14

［分析］是否需要重新设计，需比较AD与20的大小关系。即求出AD，由题意.AD=AC-CD.故先求出AC和CD。

解：在Rt∆ABC中，∠ABC＝30⁰.AB＝100

∴ AC=AB=50。BC==50

在Rt∆BCD中，i= .　 CD=10

∴ AD=AC-DC=50-10＞20.

故这条公路需要重新设计。

评注:弄清名词术语的含义，画出正确的示意图，是解题的关键。

　　　　 A　　　 C

图19-15

［例7］台风是一种自然灾害，它以台风中心为圆心在周围数十千米范围内形成气旋风暴，有极强的破坏力。据气象观测，距沿海某城市A的正南方向220km B处有一台风中心，其中心最大风力为12级，每离台风中心20km，风力就会减弱一级。该台风中心现正以15km/h的速度沿北偏东30⁰方向往C移动。且台风中心风力不变，如图19-15，若城市所受风力达到或超过4级，则称为受台风影响。

⑴ 该城市是否会受到这次台风的影响？请说明理由。

⑵ 若会受台风影响，那么台风影响该城市的持续时间有多长？

⑶ 该城市受到台风影响的最大风力为几级？

A　　　　　 C

图19-16

分析： 该城市是否会受到这次台风的影响，取决于该城市距台风中心的最近距离，若大于160km，则不受台风的影响。因风力达到或超过4级称受台风影响，故可计算出该城市从开始受台风影响到结束受台风影响之间的距离除以其速度。即为影响的时间，在离台风中心最近处风力最大。

解：⑴ 如图19-16。由点A作AD⊥BC，垂足为D。

因为AB=220. ∠B=30⁰.所以AD=AB=110.

即点A距台风中心的最近距离为110km，由题意知，

当点A距台风中心不超过160km时，将会受到台风的影响。故该城市会受到这次台风的影响。

⑵在BC上取两点E、F，使AE=AF=160，当台风中心从E处移到F处时，该城市都要受到这次台风的影响。由勾股定理得，DE=

所以EF=60(km) ,因为台风中心以15km/h的速度移动，所以这次台风影响该城市的持续时间为(h)

⑶ 当台风中心位于D处时，A市所受的这次台风的风力最大，其最大风力为12-=6.5(级)

评注:① 此类题目联系生活实际，文字长，数据多，解题时要认真读题，理解题意，注意观察实践与想象，建立数学模型(画出图形)把抽象的问题转化为解直角三角形的问题。

②此题若换成噪音干扰或航海中遭遇暗礁或沙尘暴是否影响的问题。解决问题的方法同上。具体来讲，一是正确画出图形，弄清题意；二是判断会不会受影响的标准是点A到BC的距离是否大于半径。

［例8］今年入夏以来，松花江哈尔滨段水位不断下降，达到历史最低水位。一条船在松花江某水段自西向东沿直线航行，在A处测得航标C在北偏东60⁰方向上，前进100m到达B处。又测得航标C在北偏东45⁰方向上(如图19-17)。在以航标C为圆，120m长为半径的圆形区域内有浅滩。如果这条船继续前进，是否有被浅滩阻碍的危险？( ≈1.73)

分析： 过C作CD⊥AB于D，求出CD的长。若CD＞120m，则无危险；若CD＜120m，则有被浅滩阻碍的危险。可设CD=x，利用Rt ∆ACD、Rt∆CBD结合AB=100m求解。

北　　　　　北

60⁰　　　45⁰

A　　　　 B　　　 D　　东

图19-17

解：如图19-18，过点C作CD⊥AB，垂足为D，设CD=x。

在Rt△ADC中，AD=CD·cot∠CAD=CD·cot30⁰=x　.

在Rt△BDC中，BD=CD·cot∠CBD=CD·cot45⁰= x 。

所以 AB=AD-BD= x-x=(-1)x=100

故CD=x= =50( +1)≈136.5(m)＞120m

所以，若船继续前进没有被浅滩阻碍和危险。

　　　α　　　　β

C　　　 a　　D　　　　　　 B

图19-18

评注:⑴ 这是一道现实生活会遇到的题目，解题的关键是弄清题意，将实际问题转化为数学模型，即转化为解直角三角形。⑵ 此题型可归纳为一个基本图形，如图19-18，在Rt△ABC中，CB=AB cotα……①在Rt△ADB中，DB=AB·cotβ……②　

由①-②得 CB-DB=AB(cotα- cotβ)

居民楼

新楼

　　　　　　　　　　 D　　　　　　　　　　　　　 A

32⁰

　 B　　　　　　　 C

图19-19

即 h=

［例9］如图19-19，某居民小区有一朝向为正南方向的居民楼，该居民楼的一楼是高6m的小区超市，超市以上是居民住房，在该楼的前面15m处要盖一栋高20m的新楼，当冬季正午的阳光与水平线的夹角为32⁰时，问：

① 超市以上的居民住房采光是否受影响，为什么？

②若要使超市采光不受影响，两楼应相距多少米？(结果保留整数，参考数据 sin32⁰≈,cos32⁰≈,tan32≈)

分析：① 采光是否受影响即指此时太阳光能否照射到居民家中，即太阳光照射到居民楼的高度是否大于6m。② 要不受影响，太阳光线要正好照射到居民楼底，即图中C处。

A　　　　　　　　　 D

　F　　　　　　 32⁰　 E

B　　　　　　　 C

图19-20

解：① 如图19-20，设CE=x m, 则AF=(20-x)m。

在Rt△AEF中，tan32⁰=

即 20-x=15×tan32⁰, 解得 x≈11

因为11m＞6m，所以居民住房的采光受影响。

② 如图19-21 在Rt△ABF中，tan32⁰=　　

　 32⁰

B　 15　　　C　　　　 F

图19-21

AB=20，则 BF=≈32

所以两楼应相距32m。

评注:① 解此类实际问题必须理解题意，学会建立数学模型，运用所学知识求解。② 如果题中没有给出sin32⁰.cos32⁰.tan32⁰的函数值，同学们可以使用计算器求到解题过程中需要的值。

A　　 D

B　　 C　　　　 G

图19-22

［例10］ 如图19-22，山上有一座铁塔，山脚下有一矩形建筑物ABCD，且建筑物周围没有开阔平坦地带。该建筑物顶端宽度AD和高度DC都可直接测得，从A、D、C三点都可看到塔顶端H，可供使用的测量工具有皮尺、测角器。

① 请你根据现有条件，充分利用矩形建筑物，设计一个测量塔顶到地面高度HG的方案，具体要求如下：⑴ 测量数据尽量少；⑵ 在所给图形上，画出你设计的测量平面图，并将应测数据标记在图形上(如果测A、D间距离用m表示；如果测C、D间距离用n表示，如果测角用α.β.γ表示)

② 根据你测量的数据，计算塔顶到地面的高度HG(用字母表示，测角器高度忽略不计)。

解：方案一：①如图19-23-⑴(测三个数据α.β.n)

② 解设HG=x，在Rt△CHG中，CG=x·cotβ

A　　D　α　　　　　 M

B　 C　　　　　　 G

图19-23-⑴

在Rt△DHM中，DM=(x-n)·cotα

∴ x·cotβ=(x-n)·cotα

∴ x=

方案二：① 如图19-23-⑵。(测四个数据α.γ.m.n)

② 设HG=x,在Rt△AHM中，AM=(x-n)·cotγ

在Rt△DHM中，

DM=(x-n) ·cotα

∴ (x-n)·cotγ=(x-n) ·cotα+m

∴ x=

A　 γ　　D α　　 M

　B　　　C　　　　 G

图19-23-⑵

评注:熟读题目、理解题意是解题的前提，设计方案时要尽可能和已学过的基本图形联系起来。设计的方案要科学实用。

强化训练

一、填空题：

⒈ 在Rt△ABC中，斜边AB=2。则AB²+BC²+CA²=_____________.

⒉ 若一直角三角形三边的长是三个连续的整数，那么这三边的长为_______________

⒊ 直角三角形三边长为x、3、4，则x=_____________

a　　　　 d

图19-24

⒋　等边三角形的边长是a ㎝，则它的高等于________cm

⒌ 受台风影响，马路边一棵大树在离地面6m处断裂，大树顶落在离大树底部8m处，则大树折断之前高___________m

⒍ 如图19-24 ，要修建一个育苗棚，棚宽a=3m，高b=4m，底d=10m，覆盖在顶上的塑料薄膜的面积为_______________

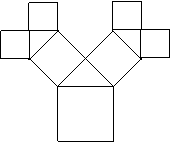
⒎ 如图19-25所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm。则正方形A、B、C、D的面积的和是____________。

　　　 B　　　　　 C

A　　　　　　　　　 D

　　　　　　　 7cm

图19-25

　　图19-26

　　 C　　　 D

B　　 F　　　　 A

图19-27

⒏ 如图19-26，是2002年8月北京第二十四届国际数学大会会标，由4个全等的直角三角形拼合而成，若图中大小正方形的面积为52和4，则直角三角形的两条直角边长分别为___________

⒐ Rt△ABC中，∠C＝90⁰.若a=4,sinA= ,则C=___________

⒑ 如图19-27，水坝横断面为梯形ABCD，迎水坝BC的坡角B为30⁰，背水坡AD坡度为1：1.5，坝顶宽DC=2米，坝高CF=4米，则坝底AB的长为_________背水坡AD长为_______。

B　　　　　　 C

图19-28

⒒ 小明想测量电线杆AB的高度，发现电线杆的影子恰好落在土坡的坡面CD和地面BC上，如图19-28，量得CD=4m，BC=10m,CD与地面成30⁰角，且此时测得1m杆的影长为2m。则电线杆的高度约为_______m(结果保留两位有效数字，≈1.41 ，≈1.73)

⒓ 一轮船以每小时20海里的速度沿正东方向航行，上午8时，该船在A处，测得某灯塔位于它的北偏东30⁰的B处(图19-29)，上午9时行至C处，测得灯塔恰好在它的正北方向，此时它与灯塔的距离是___________海里(结果保留根号)

二、选择题(四选一)

⒈ 把直角三角形两直角边同时扩大到原来的2倍，则其斜边扩大到原来的(　　　　　 )

北　　　 B

30⁰

A　　　 C　　东

图19-29

A.　2倍　　 B. 倍　 C.　 4倍　　 D.3倍

⒉ 直角三角形的周长为12cm，斜边长为5cm，则其面积为(　　　　　 )

A. 12cm²　　　B. 6cm²　　　　C. 8 cm²　　 D. 10 cm²　

⒊ 如图19-30 △ABC中，CD⊥AB于D，若AD=2BD，AC=3，BC=2，则BD的长为(　　　　　 )

A.　　 B.　　 C. 1　　 D. 　

A　　　　 D　　　　B

图19-30

⒋ 一个三角形的一边是2 m，这边上的中线为m，另两边之和为m+ m，那么这个三角形的面积是(　　　　　　 )

A. m²　　　B.m²　　　　C. m²　　　D.　 3m²　

⒌　如图19-31 两条宽为1的带子，相交成α角，那么重叠部分的面积即阴影部分面积为(　　　　　　 )

A. sinα　　 B. 　C. 　　　 D. 　

图19-31

⒍ 如图19-32，是一束平行的阳光从教室窗户射入的平面示意图，光线与地面作成角∠AMC=30⁰，在教室地面的影长MN=2米，若窗户的下檐到教室地面的距离BC=1米，则窗户的上檐到教室地面的距离AC为(　　 )

M　　　 N　　　　 C

图19-32

A. 2米　　B. 3米　　 C.　3.2米　　 D. 米

⒎ 在距楼房30m的A处测楼房BC的高，测得楼顶B的仰角为α，则楼房BC的高为(　　　　　 )m

A.30tanα　　 B. 　 C.　20sinα　　　D. 　　　

M　　　　　　　 N

　　 75⁰　　　 45⁰

A　　　 C　　　　　 B

图19-33

⒏ 如图19-33,在一个房间内，有一个梯子斜靠在墙上，梯子顶端距地面的垂直距离MA为a米，此时梯子的倾斜角为75⁰，如果梯子底端不动，顶端靠在对面的墙上，此时梯子顶端距地面的距离NB为b米，梯子的倾斜角为45⁰，这间房子的宽AB是(　　　　　　 )

A. 米　 B.米　 C. a米　　 D. b米

三、解答下列各题

1、已知一个直角三角形的斜边长为2，两直角边长的和为。

求这个直角三角形的面积。

2、在平静的湖面上有一支红莲高出水面1m，一阵风吹来，红莲吹到一边，花朵齐及水面，已知红莲移动的水平距离为2m.求这里的水深是多少？

A　　　　B

　　 C　　　　　 D

图19-34

3、如图19-34，已知∠ABC=∠BCD=90⁰.AB=6，sinA= ,CD=12,求∠D的四个三角函数值。

4、如图19-35，在△ABC中，∠A=30⁰，tanB=　 BC=,求AB的长

5、已知如图19-36所示，折叠矩形的一边AD使点D落在BC边的点F处，已知AB=8cm，BC=10cm，求EC的长。

6、一艘渔船正以每小时30海里的速度由西向东航行，在A处看见小岛C在船的北偏东60⁰，40分钟后，渔船行至B处，此时看见小岛C在船的北偏东30⁰。若以小岛C为中心周围10海里是危险区，问这艘渔船继续向东航行是否有进入危险区的可能？

A　　　　　　　　　　 B

图19-35

A　　　　　　　　　　 D

B　　　　 F　　　　 C

图19-36

G　　　　　　 C

B　　　　 E　D F

图19-37

7、如图19-37，城市规划期间，欲拆除一电线杆AB，已知距电线杆水平距离14m的D处有一大坝，背水坡CD的坡度i=2:1，坝高CF=2 m，在坝顶C处测得杆顶A的仰角为30⁰，D、E之间是宽为2m人行道，试问在拆除电线杆AB时，为确保行人安全，是否需要将此人行道封上？请说明理由。

A　　　　　　　 C

图19-38

8、如图19-38，小丽的家住在成都市锦江河畔的电梯公寓AD内。她家的河对岸新建了一座大厦BC，为了测得大厦的高度，小丽在她家的楼底A处测得大厦顶部B的仰角为60⁰，爬上楼顶 D处测得大厦顶部B的仰角为30⁰。已知小丽所在的电梯公寓高82米。请你帮助小丽计算出大厦高度BC及大厦与小丽所住的电梯公寓间的距离AC。

第25部分《解直角三角形》综合测试题A

一、填空题：(每空2分，共30分)

1、　sin²30⁰+cos²30⁰=___________

2、　计算：(sin30⁰)^-1-(cot60⁰)⁰=______________

3、　已知 cosA-=0，则锐角∠A=___________度

4、　Rt△ABC中，∠C=90⁰，AB=17，sinA=，则BC=___________

B　　　 D　　　　　 A

图19-1

5、　如图19-1，在△ABC中，∠ACB=90⁰，BC=4，AC=5，CD⊥AB，

则 sin∠ACD=_______，tan∠BCD=_________

6、　在Rt△ABC中，∠C=90⁰，b：a=1：，则cos(90⁰-A)=_____________

C　　　　　 A

图19-2

7、　如图19-2是河堤的横断面，堤高BC=5m，迎水斜坡AB的坡度为1：2，那么AB的长为___________m

8、　等腰三角形一腰上的高与另一腰的夹角为30⁰，腰长为a，则其底边上的高是_________

9、已知直角三角形的两直角边之和为2，面积为2，则该直角三角形的斜边长为_______

10、　　　　油田高级中学升国旗时，李明同学站在离旗杆底部12米处行注目礼，当国旗升至旗杆顶端时，该同学视线的仰角恰为45⁰，若他的双眼离地面1.3米，则旗杆的高度是________米。

11、已知∠A为锐角，cotA=　则sin =__________

12、用计算器计算cos35⁰=__________(保留两个有效数字)

20米　120⁰　　 30米

图19-3

13、一船向西航行，上午9时30分在小岛A南偏东30⁰的B处，已知AB为60海里，上午11时整，船到达小岛A的正南方向，则该船的航行速度为____________

14、学校校园内有一块如图19-3所示的三角形空地，计划将这块空地建成一个花园，以美化校园环境，预计花园每平方米造价为30元，学校建这个花园需要投资_____________元(精确到1元)

二、选择题(四选一)(每小题3分，共24分)

15 、△ABC中，∠C=90⁰，BC=2，AB=3，则下列结论中正确的是(　　　　　 )

A. sinA=　 B. cosA=　　 C.　sinA=　　 D.tanA=

16、在△ABC中，∠A、∠B都是锐角，且sinA-+ =0，则△ABC的形状是(　　　　 )

A. 直角三角形　 B. 钝角三角形　　　C. 锐角三角形　　　 D. 等腰三角形

17、在△ABC中，∠C=90⁰，a、b、c分别是∠A、∠B、∠C的对边，则下列等式成立的是(　　　　　 )

A.b=c·cosA　　B. b=a·sinB　　C. a=b·tanB　 D. b=c·cotA

18、已知∠A为锐角，且cosA≤　　,那么(　　　　　　　　 )

A 　　　　　　　　C

　　　　图19-4　　　

A.　0⁰＜A≤60⁰　　 B. 60⁰ ≤A＜90⁰　　C.　0⁰＜A≤30⁰　　 D. 30⁰≤A ＜90⁰

19、如图19-4，Rt△ABC中，∠ACB=90⁰，CD⊥AB于D，BC=3，AC=4，设∠BCD=α，则tanα的值为(　　　　　 )

A. 　 B.　　C.　　　 D.

20、如图19-5，Rt△ABC中，∠C=90⁰，D为BC上一点，

∠DAC=30⁰，BD=2，AB=2,则AC的长是(　　　　　　　　 )

A. 　　　B.2　　 C. 3　　D.

B　　　　　　　 D

图19-6

C　　　D　　　　　　 B

图19-5

A　　　　6

图19-7

21、如图19-6，两建筑物的水平距离为a m，从A点测得C点的俯角为α，测得D点的俯角为β,则较低建筑物CD的高为(　　　　　 )

A. a m　　 B.atanα m　　C. a cotαm　 D. a(tanβ-tanα)m

B　　　 E　　　　C

图19-8

22、如图19-7是一块长宽高分别为6cm、4cm和3cm的长方体木块，一只蚂蚁要从长方体木块的一个顶点A处沿着长方体的表面到长方体上和A点相对的顶点B处吃食物，那么它需要爬行的最短路径的长是(　　　　　　)

A.(3+2)cm　B.cm　C. cm　 D.9 cm　

三、解答题：(共46分)

23、(8分)如图19-8，D是△ABC的边AC上一点，CD=2AD，AE⊥BC，交BC于点E，若BD=8，sin∠CBD=　求AE的长。

　　　　　　　　 D　　　　 C

　 C^/　　　　　　 B^/

　a　　c　　　　　　 c　　b

D^/　b　　A　 a　　　 B　　　　　　　　　　　　　　

图19-9

24、(6分)如图19-9，设火柴盒ABCD的两边之长为a和b，对角线长为c，推倒后的火柴盒是AB^/C^/D^/，试用该图形验证勾股定理的正确性。

25、(10分) (参考数据：sin65⁰≈0.9,cos65⁰≈0.4，tan65⁰≈2.1,≈1.4) 如图19-10，某海滨浴场岸边可近似地看成直线，位于岸边A处的救生员发现海中B处有人求救，1号救生员没有直接从A处游向B处，而是在岸边自A处跑300米到距离B最近的D处，然后游向B

45⁰　　　 65⁰

A　　　　 C　　　 D海岸

图19-10

处；假定所有的救生员在岸边的跑行的速度这6米/秒，在海中游进的速度为2米/秒，∠BAD=45⁰。

① 请根据以上条件分析1号救生员的选择是否正确；

② 若2号救生员同时从A处在岸边跑到C处，再游向B处，已知∠BCD=65⁰，问哪位救生员先赶到B处救人？(为了便于计算，计算过程中的数值均可精确到0.1)。

26、(10分) 细心观察图形，认真分析各式，然后解答问题：

1　A₆

　　　　　 1 A₅

　　　　　　　 S₆　S₅　1 A₄　　　　　　　　　　　　　　　　　 S₄　　1A₃

　　　　　　　　　　 S₃1

　　　　　　　　　　　 S₂　　 A₂

　　　　　　　　　　　　 S₁　 A₁　　　　　　

图19-11

()²+1=2，S₁=；

()²+1=3，S₂=；

()²+1=4，S₃=；

……　　　　　 ……

① 请用含有n(n为正整数)的等式表示上述变化规律；

② 推算出OA₁₀的长

③ 求出S₁²+ S₂²+ S₃²+…+ S₁₀²的值。

　　 C　　　　　　　　　　　　　 B

A　　　　　　　　　　　　　 D

图19-12

27、(12分) 如图19-12。公路AB和铁路CD在点P处交汇，且∠BPD=60⁰，点Q在∠BPD的平分线上，且在Q点处有一疗养院，PQ=240米，设大型运输车在行驶时。110米范围内都会受到噪声影响，火车在铁路上行驶时，周围200米以内都受噪声影响。

① 当大型运输车和火车分别沿PB、PD方向行驶时，疗养院是否会受到噪声的影响？请你与同学交流说明理由。

② 如果受到影响，已知大型运输车的平均速度为60千米/小时，火车的平均速度为90千米/小时，那么疗养院影响的时间为多少秒？

③ 如果公路AB上大型运输车的通过率为10辆/小时，铁路CD上火车的通车率为5列/小时，请你计算一下该疗养院是否应该搬迁，并说明理由。

第25部分《解直角三角形》综合测试题B

　　 A　　　　　　　 C

图19-1

一、填空题：(每空2分，共30分)

1、　如图19-1，正方形A的面积是16，正方形的面积B为9，那么正方形C的面积为_______

2、　计算：cos45⁰+tan60⁰-sin30⁰=_____________

3、　若α为锐角，且cosα=sin40⁰，则α=____________

4、　已知tan(40⁰-2α)=cot(80⁰+α)，则tanα=________

5、　用计算器计算sin18⁰=_______________

图19-2

6、计算：2sin60⁰-( )^-1+(-1)⁰=___________

7、如图19-2，一个小球由地面沿着坡度为i=1:2的坡面向上前进10米，此时小球距离地面的高度为_________________

8、如图19-3，P是OA上一点，且P点在坐标为(3，4)，则sinα=___________

　 O　　 3　　　　 x

图19-3

9、　在Rt△ABC中，∠C=90⁰， sinA= ,则sinB=____________

10、　在Rt△ABC中，∠C=90⁰，a=2, sinA=,则c=____________

11、　在△ABC中，已知∠B为锐角，AB=2cm，BC=5cm，S_△ABC=4cm²，则cosB=__________

　　　　　　　　　　　　　 20米

30⁰

图19-4

12、　　已知△ABC中，∠C=90⁰，则tan=____________

13、　青岛位于北纬36⁰4^/，通过计算可以求得，在冬至日正午的太阳入射角为30⁰(如图19-4)，因此，在规划建设楼高为20米的小区时，两楼间的距离最小为___________米，才能保证不挡光？(结果保留四位小数)

A　　　　　　　 C

图19-5

14、　如图19-5，某建筑物BC直立于水平地面，AC=9米，需建造阶梯AB，使每阶高不超过20cm，则此阶梯最少需要建________阶(最后一阶的高若不是20cm，按一阶计算)。

15、　如图19-6，小明将一张矩形纸片ABCD沿CE折叠，B点恰好落在AD边上，设此点为F，若AB：BC=4：5，则cos∠DCF的值为__________

D　　　　　　 C

A　　　E　　　 B

图19-6

二、选择题(每小题3分，共24分)(四选一)

16、　设直角三角形的边长分别为a、b、c，那么a：b：c不可能等于(　　　　 )

A. 3：5：4　　　B.　5：12：13　　 C.　2：3：4　　　D. 8：15：17

17、　在Rt△ABC中，如果各边的长度扩大2倍，那么锐角∠A的各三角函数值

A. 不变　 B.　扩大2倍　　 C.　缩小2倍　　D. 不能确定

18、　若sinα-cosα=m　则sinα·cosα的值为(　　　　 )

A.1+m²　 B.1-m²C. (1+m²)　 D. (1-m²)

C　　　　 E　　　　　 D

图19-7

19、　　　　如图19-7，CD是平面镜，光线从A点出发经CD上点E反射后照射到B点，若入射角为α(入射角等于反射角)。AC⊥CD，BD⊥CD，垂足分别为C、D。且AC=3，BD=6，CD=11，则tanα的值为(　　　　　 )

A.　　B.　　 C.　　　　D.

20、　在Rt△ABC的斜边AB上另作Rt△ABD，并以AB为斜边，若BC=1，AC=b，AD=2，则BD的长为(　　　　　　 )

A.　 B. 　　C. +2　　　D.

　　　图19-8

21、　　　　育人中学的师生准备测量某段渠水的深度，他们把一根竹竿插到离岸边1米远的水底，只见竹竿高出水面1尺，把竹竿的顶端拉向岸边，竿顶和岸边的水面刚好相齐，如图19-8，则渠水的深度与竹竿的长度分别为

A　　　　　　 D

45⁰　　　 120⁰

B　　　　　　 C

图19-9

A. 5米，4米 B. 5尺，4尺　　 C. 1尺，2尺　　D.1米，2米

22、　已知，如图19-9，梯形ABCD中，AD∥BC，∠B=45⁰，∠C=120⁰，AB=8，则CD的长为(　　　 )

A.　 B.4　　　 C.　　　 D.4

23、　已知在Rt△ABC中，∠C=90⁰，则关于x的一元二次方程x²cotA-2x+cotB=0的根的情况是(　　　　　　　　 )

45⁰　　　　　　28⁰

A　　 B　　　　　　　 C

图19-10

A. 有两个不相等的实数根　　B. 有两个相等的实数根　　　 C.　没有实数根　　　 D. 根的情况由∠A、∠B的值确定。

三、解答题：(共46分)

B　　　　　　　 C

图19-11

24、　 (7分)如图19-10。A、B、C三个村庄在一条东西走向的公路上，AB=2千米，在B村的正北方向有一个D村，测得∠DAB=45⁰，∠DCB=28⁰，今将△ACD区域进行规划，除其中面积为0.5平方千米的水塘外，准备把剩余区域的一半作绿化用地，试求绿化用地的面积(结果精确到0.1平方千米，sin28⁰=0.4695,cos28⁰=0.8829,tan28⁰=0.5317,cot28⁰=1.8808)

25、　 (7分)某片绿地的形状如图19-11，∠A=60⁰。AB⊥BC， AD⊥CD，AB=200m，CD=100m，求AD、BC的长(精确到1m，≈1.732)

26、　 (8分) 某村计划开挖一条长为1500m的水渠，渠道的断面为等腰梯形，渠道深0.8m，下底宽1.2m，坡度为45⁰，(如图19-12)，实际开挖渠道时，每天比原计划多挖土20m³,结果比原计划提前4天完工，求原计划每天挖土多少立方米？