一 数与代数
第一单元
第1课 实 数
1．4的算术平方根是 ，│-（-2.5）│= .
2．-3到3之间的所有整数的和是 .
3．函数
中，x的取值范围是 .
4．某食品包装袋上标有500±0.02g，它表示 .
5．任意实数x，经过以下运算过程 
，
那么当x=3时，运算结果是 .
6．一个数的绝对值的相反数是-
，则这个数是 .
7．-
的倒数等于 .
8．π精确到十分位得到的近似数是 _.
9．我国土地面积约为960万平方千米，用科学记数法表示正确的是 （ ）
A．0.96×10
万平方千米 B．9.6×10
万平方千米
C．9.6×10平方千米 D．9.6×10万平方千米
10．
代简的结果是
（ ）
A．-3 B．3 C．±3 D．9
11．在-4，sin45°，
，-
，0这五个数中，有理数的个数是
（ ）
A．2个 B．3个 C．4个 D．5个
12．若a、b互为相反数，则在⑴a+b＞0，⑵ab=1，⑶│a│=│b│，⑷a=-b，⑸a2=b2中一定成立的有 ( )
A．2个 B．3个 C．4个 D．5个
13．一个数的倒数与这个数的绝对值的和等于零，那么这个数是 （ ）
A．1 B．-1 C．1和-1 D．0
14．若abc>0，a<b，ab<0，则下列结论正确的是 （ ）
A．a＜0，b＜0，c＞0 B．a＜0，b＞0，c＜0
C．a＞0，b＜0，c＞0 D．a＜0，b＞0，c＞0
15．如果实数m、n，有m+n＜0，mn＜0，那么下列不等式中正确的是 （ ）
A．│m│≥│n│ B．│m│＜│n│
C．当m＞0，n＜0时，│m│＞│n│ D．当m＜0，n＞0时，│m│＞│n│
16．a、b的数在数轴上的位置如图所示，则下列结论正确的是 （ ）
 |
A．
<b<
<a B．<a<<b
C．a<<<b D．a<<b<
17．计算:
（1）1-18×（
）-1+（-6）2 ； （2）2-2tan45°+（
-25）
；
（3）
； （4）
.
18．将-（+3），1，0，-1.5，2
及它们的相反数在数轴上表示出来，并用“<”将它们连接起来.
19．已知│a│=3，│b│=4，且a<b，求a+b的值.
20．已知
，求
的值.
第2课 整式（含因式分解）
1．单项式
与3x2y是同类项，则
的值为
（ ）
A．
B.
C. 
D.
2．因式分解
的结果等于
（ ）
A．
B.
C. 
D. 
3．下列各式中正确的是 （ ）
A．
B.
C. 
D. 
4.已知方程组
的解为
,则
的值为
( )
A．4.5 B. 3.5 C.-3 D. 2.5
5．已知
，则
，
，
（ ）
A．
B.
C. 
D. 
6. 
，则
,
,
的大小关系
( )
A．
B.
C. 
D. 
7.如图，根据下表所反映的规律，第n行第n列的数应为 （ ）
| 第1列 | 第2列 | 第3列 | 第4列 | ||
| 1 | 2 | 3 | 4 | … | 第1行 |
| 2 | 3 | 4 | 5 | … | 第2行 |
| 3 | 4 | 5 | 6 | … | 第3行 |
| 4 | 5 | 6 | 7 | … | 第4行 |
| ： | ： | ： | ： |
A.2n-1 B.2n+1 C.n2-1 D.n2
8.某县今年的小麦产量为112万吨，用科学记数法表示为 千克.
9.若
是整式
的一个因式，则
= .
10.计算
.
11.因式分解（1）
＝
（2）
12.化简
.
13.
.
14.已知多项式：
．
(1)按规律写出该多项式的第6项，并指出它的系数和次数．
(2)这个多项式是几次几项式?
15.观察下列一组单项式
┅┅
，┅你能写出第n个单项式吗？并写出第2007个单项式.
16．分别根据所标尺寸，用因式乘积的形式表示下列图形中有阴影部分的面积.
|
|
第3课 分 式
1．当x 时，分式
有意义.
2．当x 时，分式
的值为零.
3．写一个分式，使x＝2时分式无意义，且x＝1时分式值为0，这样的分式可以是 （任意写一个）；当x＝ 时，该分式的值为－1.
4．计算：
＝
.
5．若
，则
＝
；若
，则
＝
.
6．若
，则
＝
，
＝ .
7．
＝1，则
的值为
.
8．若实数、
满足
，则
的值为
.
9．计算
的结果为
（ ）
A．1 B．x＋1 C．
D．
10．若分式
中的x、y的值都变为原来的3倍，则此分式的值 （ ）
A．不变 B．是原来的3倍
C．是原来的
D．是原来的
11．下列运算，结果正确的是 （ ）
A．
B．
C．
D．
12．不改变分式
的值，把它的分子和分母中的各项系数都化为整数，则所得结果为
( )
A．
B．
C．
D．
13．化简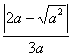
的值为
（ ）
A．或－1 B．
C．或1
D．1或－1
14．若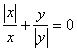
，则下列结论正确的是
（ ）
A．x、y为一切实数 B．xy＞0 C．xy＝0 D．xy＜0
15．、为实数，且≠0，＋≠0，则
应等于
（ ）
A． B．
C．
D．
16．、为实数，＝1，设m＝
，n＝
，则m、n的大小关系为
（ ）
A．m＞n B．m＜n C．m=n D．无法确定
17．计算：
．
18．化简，再选取一个你喜爱的值代入求值
．
19．已知
，
，求代数式
的值．
20．已知：
，求
第4课 二次根式
1．
的绝对值是 ，当 时，
有意义，若
有意义，则
.
2．当m>n时，
＝ ，当 时，
.
3．化简
，
.
4．若最简二次根式
与－
是同类二次根式，则x=
.
5．在实数范围内分解因式
.
6．已知矩形长为
cm，宽
为cm ，那么这个矩形对角线长为
cm.
7．计算
_，
.
8．若
，则
.
9．把根式
根号外的移到根号内，得
.
10．若代数式
有意义，则的取值范围是
（ ）
A.
B.
C.
D.
11．下列运算正确的是 （ ）
A.
B.
C.
D.
12．下列根式中，最简二次根式是 ( )
A.
B.
C.
D.
13．若
，则的取值范围是
( )
A.x≥
B.x≤ C.x> D.x<
14. 若x<2，化简
的正确结果是
（ ）
A.-1 B.1 C.2x-5 D.5-2x
15. 已知
，则
的值为
( )
A.
B.
C.
D.
16.（1）
（2）
（3）
17. 已知x为奇数，且
的值.
18.甲、乙两人对题目“化简并求值：
，其中
”有不同的解答，甲的解答是:
,乙的解答是:
,谁的解答是错误的？为什么？
第一单元 数与式单元检测卷
（总分100分，时间60分钟）
一．选择题（本题共10小题，每小题3分，共30分）
1．如果与－2的差为0，那么是
（ ）
A．2 B． C．－ D．－2
2．已知分式
的值是零，那么的值是
（ ）
A．－1 B．0 C．1 D．±1
3．2007年，中国月球探测工程的“嫦娥一号”卫星将发射升空，飞向月球.已知地球距离月球表面约为38400千米，那么这个距离用科学记数法（保留三个有效数字）表示应为 （ ）
A．
千米 B．
千米
C．
千米 D．
千米
4．下列运算中，正确的是 （ ）
A．
B．
C．
D．
5．实数
0．……中，无理数有
（ ）
A．1个 B．2个 C．3个 D．4个
6．一批货物总重
，下列可将其一次性运走的合适的运输工具是 （ ）
A．一艘万吨级巨轮 B．一架飞机
C．一辆汽车 D．一辆板车
7．下列运算正确的是 （ ）
A．
B．
C．
D．
8．二次三项式
可在整数范围内因式分解，那么整式
的取值可以有（ ）
A．2个 B．4个 C．6个 D．无数个
9．已知
为实数，且＝1，设
，
，则M，N的大小关系是
（ ）
A．M＞N B．M＝N C．M＜N D．M≥N
10．若化简
的结果为
，则取值范围是 （
）
A．为任意实数 B．
C．
D．
二．填空题（本题共10小题，每小题3分，共30分）
11．当m＜3时，
．
12．计算：
．
13．方程
的解是
．
14．用“※”定义新运算：对于任意实数，，都有※＝
例如，7※4＝4
＝17，那么5※3＝
；当m为实数时，m※（m※2）＝
．
15．写出一个有理数和一个无理数，使它们都是大于－2的负数： ．
16．把
分解因式的结果是
．
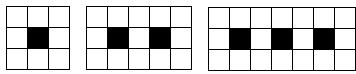17．下列图案由边长相等的黑、白两色正方形按一定规律拼接而成，依此规律，第5个图案中白色正方形的个数为
．
18．化简：
＝
．
19．依法纳税是公民应尽的义务．《个人所得税法》规定：每月总收入减去1600元后的余额为应纳税所得额，应纳税所得额不超过500元的按5%纳税；超过500元但不超过2000元的部分按10%纳税，……若职工小王某月税前总收入为2000元，则该月他应纳税 元．
20．已知
，
，且
，则
的值等于
．
三．解答题（第17题每小题5分，第18题6分，第19题、20题每题7分，第21题10分，共40分）
17．（1）计算：
；
（2）化简，求值：
，其中
，
．
18．如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘数” ．如
，
，
，因此4，12，20这三个数都是神秘数．
（1）28和2012这两个数是神秘数吗？
（2）设两个连续偶数为
和
（其中
取非负整数）．由这两个连续偶数构造的神秘数是4的倍数吗？为什么？
（3）两个连续奇数的平方差（取正数）是神秘数吗？为什么？
19．老师在黑板上写出三个算式：
，
，
，王华接着又写了两个具有同样规律的算式：
，
，……
（1）请你再写出两个（不同于上面算式）具有上述规律的算式；
（2）用文字写出反映上述算式的规律；
（3）证明这个规律的正确性．
20．已知A＝
，B＝2，C＝
，其中＞1．
（1）求证：A－B＞0；
（2）试比较A．B．C三者之间的大小关系，并说明理由．
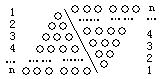
21．我国著名数学家华罗庚说过：“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休”．数学中，数和形是两个最主要的研究对象，它们之间有着十分密切的联系，在一定条件下，数和形之间可以相互转化，相互渗透．
数形结合的基本思想，就是在研究问题的过程中，注意把数形结合起来考察，斟酌问题的具体情形，把图形性质的问题转化为数量关系的问题，或者把数量关系的问题转化为图形性质的问题，使复杂问题简单化，抽象问题具体化，化难为易，获得简便易行的成功方案．
例如，求1+2+3+4+…+n的值，其中n是正整数．
对于这个求和问题，如果采用纯代数的方法（首尾两头加），问题虽然可以解决，但在求和过程中，需对n的奇偶性进行讨论．
如果采用数形结合的方法，即用图形的性质来说明数量关系的事实，那就非常的直观.现利用图形的性质来求1+2+3+4+…+n的值，方案如下：如图，斜线左边的三角形图案是由上到下每层依次分别为1，2，3，…，n个小圆圈排列组成的.而组成整个三角形小圆圈的个数恰为所求式子1+2+3+4+…+n的值.为求式子的值，现把左边三角形倒放于斜线右边，与原三角形组成一个平行四边形.此时，组成平行四边形的小圆圈共有n行，每行有（n+1）个小圆圈，所以组成平行四边形小圆圈的总个数为n（n+1）个，因此，组成一个三角形小圆圈的个数为
，即1，2，3，…，n＝．
（1）依照上述数形结合的思想方法.设计相关图形，求1+3+5+7+…+（2n－1）的值，其中n是正整数.（要求：画出图形，并利用图形做必要的推理说明）
（2）试设计另外一种图形，求1+3+5+7+…+（2n－1）的值，其中n是正整数．（要求：画出图形，并利用图形做必要的推理说明）
