§7．1 数据的收集和处理
★课标视点 把握课程标准, 做到有的放矢
1. 从事收集、整理、描述和分析数据的活动，能用计算器处理较为复杂的统计数据。
2. 通过丰富的实例，感受抽样的必要性，能指出总体、个体、样本，体会不同的抽样可能得到不同的结果。
3. 能根据问题查找有关资料，获得数据信息；对日常生活中的某些数据发表自己的看法。
4. 认识到统计在社会生活及科学领域中的应用，并能解决一些简单的实际问题。
5. 在具体情境中理解并会计算加权平均数；根据具体问题，能选择合适的统计量表示数据的集中程度。
6. 探索如何表示一组数据的离散程度，会计算极差和方差，并会用它们表示数据的离散程度。
7. 通过实例，体会用样本估计总体的思想，能用样本的平均数、方差来估计总体的平均数和方差。
★课标解读 把握知识建构, 拓展技能方法
★ 案例导学 题型归纳引路, 做到各个击破
知识系统图
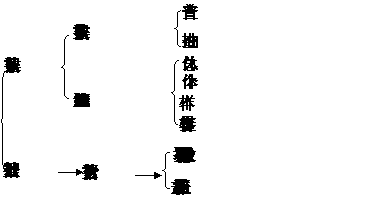
技能和方法
1．平均数、众数、中位数反映数据的特征的区别与联系
2．方差和 标准差的区别与联系
3．加权平均的作用可以加强有些数据的“重要性”
【题型一】统计的有关概念
【例1】
|
（1）调查全省食品市场上某种食品的色素含量是否符合国家标准
（2）调查某城市某天的空气质量
（3）调查你所在班级全体学生的身高
（4）调查全省初中生每人每周的零花钱数
【解】（1）抽样调查（2）抽样调查（3）普查（4）抽样调查
【导学】一般来讲，要求全面了解数据，且总数较少时，用普查的方式好；要求全面了解数据且总数较多时，采用抽样调查好.
【例2】为了解一年某商场每天上午顾客人数，抽查了其中20天的每天上午的顾客人数，在这个问题中，总体、个体和样本分别是什么？
【解】 总体是一年某商场每天上午顾客人数情况的全体；个体是某商场每天上午顾客人数的情况；样本是所抽取的20天每天上午的顾客人数情况.
【导学】弄清考察对象是明确总体、个体、样本的关键，总体、个体、样本的考察对象是同一的，所不同的是范围不同.
【题型二】调查方案设计
【例3】某市电视台为了更好的编排节目，想了解观众的喜好情况，他们派出一名工作人去调查50名观众，这名工作人员来到一个中学调查了50名同学，你认为这样选取样本合适吗？为什么？
【解】 不合适.这样选取的样本不是随机抽取的，不具有代表性和广泛性.
【导学】抽样调查的对象是随机抽取的，要注意样本的广泛性和代表性.
【题型三】统计特征数的应用
【例4】(2006 江西)一次期中考试中，A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示：（单位：分）
| A | B | C | D | E | 平均分 | 标准差 | |
| 数学 | 71 | 72 | 69 | 68 | 70 |
| |
| 英语 | 88 | 82 | 94 | 85 | 76 | 85 |
（1）求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差；
（2）为了比较不同学科考试成绩的好与差，采用标准分是一个合理的选择，标准分的计算公式是：标准分＝（个人成绩－平均成绩）÷成绩标准差。
从标准分看，标准分大的考试成绩更好。请问A同学在本次考试中，数学与英语哪个学科考得更好？
【解】（1）数学考试成绩的平均分
英话考试成绩的标准差
(2)设A同学数学考试成绩标准分为P
，英语考试成绩标准分为P
，则
P =
P
P> P ，
从标准分看，A同学数学比英语考得更好
.
【导学】一组数据的标准差计算公式是S＝
，其中
为n个数据
、
…
的平均数。
★智闯三关 发挥聪明睿智,关公怎比我强
核心知识----基础关
1．下列调查方式，你认为正确的是 ( B )
A. 了解一批炮弹的杀伤半径，采用普查方式；
B. 了解南安市每天的流动人口数，采用抽查方式；
C. 要保证“神舟6号”载人飞船成功发射，对重要零部件采用抽查方式检查；
D. 了解南安市居民日平均用水量，采用普查方式．
2．下列调查，比较适2用普查而不适用抽样调查方式的是（C）
A．调查全省食品市场上某种食品的色素含量是否符合国家标准；
B．调查一批灯泡的使用寿命；
C．调查你所在班级全体学生的身高；
D．调查全国初中生每人每周的零花钱数.
【提示】只要有一个班的人数就可以办到,容易操作.
3．去年娄底市有7.6万学生参加初中毕业会考，为了解这7.6万名学生的数学成绩，从中抽取1000名考生的数学成绩进行统计分析，以下说法正确的是（ C ）
A．这1000名考生是总体的一个样本
B．7.6万名考生是总体
C．每位考生的数学成绩是个体
D．1000名学生是样本容量
【提示】统计中，考察的对象是数据。
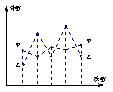4.右图是甲、乙两位同学的5次数学考试的成绩
的折线统计图，你认为成绩较稳定的是( A )
A.甲 B.乙
C.甲、乙的成绩一样稳定 D.无法确定
【提示】波动小的为标准,甲稳定.
5.小伟五次数学考试成绩分别为：86分、78分、80分、85分、92分，李老师想了解小伟数学学习变化情况，则李老师最关注小伟数学成绩的 ( D )
A．平均数 B．众数 C．中位数 D．方差
6. 某班在一次数学测试后，成绩统计如下表：
| 分数 | 100 | 90 | 80 | 70 | 60 | 50 |
| 人数 | 7 | 14 | 17 | 8 | 2 | 2 |
该班这次数学测试的平均成绩是（ A ）
A、82 B、75 C、65 D、62
【提示】
7．为了了解汽车司机遵守交通法规的意识，小明的学习小组成员协助交通警察在某路口统计的某个时段来往汽车的车速（单位：千米/小时）情况如图所示。根据统计图分析，这组车速数据的众数和中位数分别是（ C ）
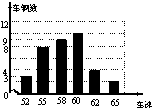A、60千米/小时，60千米/小时
B、58千米/小时，60千米/小时
C、60千米/小时，58千米/小时
D、58千米/小时，58千米/小时
【提示】观察可知，3个52，8个55，9个58，10个60，4个62，2个65
8．若一组数据1，2，3，x的极差为6，则x的值是（ Ｄ ）
A．7 B．8 C．9 D．7或－3
【提示】极差=最大－最小
9．（）某青年排球队12名队员的年龄情况如下：
| 年龄（单位：岁） | 18 | 19 | 20 | 21 | 22 |
| 人 数 | 1 | 4 | 3 | 2 | 2 |
则这个队队员年龄的众数和中位数是 （ A ）
Ａ．19，20 Ｂ．19，19 Ｃ．19，20.5 Ｄ．20，19
【提示】数据的个数为偶数时,中位数为中间的两个数的平均值.
核心能力-----技能关
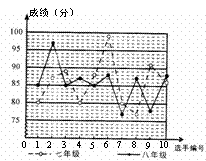10．某城区举行“八荣八耻”演讲比赛，中学组根据初赛成绩在七，八年级分别选出10名同学参加决赛，这些选手的决赛成绩如图所示：
| 团体成绩 | 众数 | 平均数 | 方差 |
| 七年级 |
|
| |
| 八年级 |
|
|
根据图和左表提供的信息，解答下列问题：
|
（2）考虑平均数与方差，你认为 年级的团体成绩更好些；
（3）假设在每个年级的决赛选手中分别选出3人参加总决赛，你认为哪个年级的实力更强一些，请说明理由．
解：（1）七年级众数是80，八年级众数是85
（2）八
（3）解法一：七年级前三名总分：
分
八年级前三名总分：
分
七年级实力更强些
解法二：由图可以看出七年级的第一、二、三名的分数分别比八年级的一、二、三名分数高
所以七年级更强些
11．某中学开展“八荣八耻”演讲比赛活动，初三（1），三（2）班根据初赛成绩各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩（满分为100分）如下图所示．
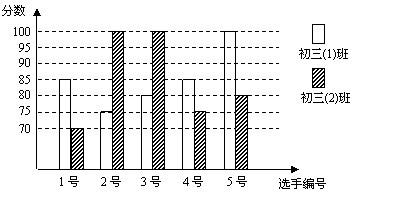
（1）根据上图填写下表
| 平均数（分） | 中位数（分） | 众数（分） | |
| 初三（1）班 | 85 | 85 | |
| 初三（2）班 | 85 | 80 |
（2）结合两班复赛成绩的平均数和中位数分析哪个班级的复赛成绩较好．
（3）如果在每班参加复赛的选手中分别选出2人参加决赛，你认为哪个班的实力更强一
些，并说明理由．
解：（1）85；100．
（2）解： 两班的平均数相同，初三（1）班的中位数高， 初三（1）班的复赛成绩好些．
（3）解： 初三（1）班、初三（2）班前两名选手的平均分分别为92.5，100分，
在每班参加复赛的选手中分别选出2人参加决赛，初三（2）班的实力更强一些．
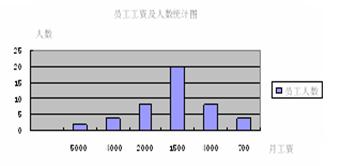
12．某公司员工的月工资情况统计如下表：
| 员工人数 | 2 | 4 | 8 | 20 | 8 | 4 |
| 月工资（元） | 5000 | 4000 | 2000 | 1500 | 1000 | 700 |
（1）分别计算该公司员工月工资的平均数、中位数和众数；
（2）你认为用（1）中计算出的哪个数据来代表该公司员工的月工资水平更为合适？请简要说明理由；
（3）请画出一种你认为合适的统计图来表示上面表格中的数据．
解：（1）平均数为
（元）．
中位数为
元． 众数为元．
（2）（答案不唯一，合理即可）
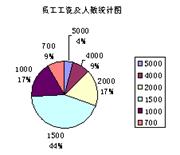（3）．
13．饮料店为了了解本店罐装饮料上半年的销售情况，随机调查了8天该种饮料的日销售量，结果如下（单位：听）：33 ，32 ，28 ，32 ，25 ，24 ，31 ，35．
(1)这8天的平均日销售量是多少听?
(2)根据上面的计算结果，估计上半年(按181天计算)该店能销售这种饮料多少听？
解：（1）这8天的平均日销售量是：
（听）
30×181=5430.
估计上半年(按181天计算)该店能销售这种饮料5430听
14．某单位欲从内部招聘管理人员一名，对甲、乙、丙三名候选人进行了笔试和面试两项测试，三人的测试成绩如下表所示：
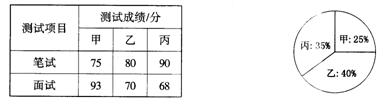
根据录用程序，组织200名职工对三人利用投票推荐的方式进行民主评议，三人得票率（没有弃权票，每位职工只能推荐1人）如上图所示，每得一票记作1分．
(l）请算出三人的民主评议得分；
(2）如果根据三项测试的平均成绩确定录用人选，那么谁将被录用（精确到 0.01 )?
(3）根据实际需要，单位将笔试、面试、民主评议三项测试得分按 4 : 3 : 3 的比例确定个人成绩，那么谁将被录用？
解：(l)甲、乙、丙的民主评议得分分别为：50 分，80 分，70 分．
(2）甲的平均成绩为
（分）,
乙的平均成绩为：
（分）,
丙的平均成绩
（分）
由于76.67>76>72.67，所以候选人乙将被录用.
(3）如果将笔试、面试、民主评议三项测试得分按4 : 3 : 3的比例确定个人成绩，那么
甲的个人成绩为：
72.9（分）,
乙的个人成绩为：
77（分）
丙的个人成绩为：
77.4（分）
由于丙的个人成绩最高，所以候选人丙将被录用．
核心精神---创新关
16．
 |