中考数学模拟试题（12）
说明：考试时间90分钟，满分120分．
一、选择题（本题有10小题，每题3分，共30分）
每小题给出4个答案，其中只有一个是正确的．
1、光年是天文学中的距离单位，1光年大约是9 500 000 000 000km，这个数字用科学记数法可表示为( )
(A) 950×1010 km (B) 95×1011 km (C) 9.5×1012 km (D) 0.95×1013 km
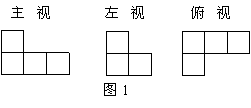2、如图1是由一些相同的小正方体构成的几何体的三视图，这些相同的小正方体的个数是（ ）
（A）4个 （B）5个 （C）6个 （D）7个
3、下列计算正确的是 （ ）
（A）(-2)0＝－1 （B）－23＝－8
（C）－2－(－3)＝－5 （D）3－2=-6
4、在下列图形中，即是轴对称图形，又是中心对称图形的是（ ）
 |
（A） (B) (C) (D )
5、要使二次根式
有意义，字母x必须满足的条件是（ ）
（A）x≤2 （B）x＜2 （C）x≤－2 （D）x＜－2
6、对“五·一”黄金周7天假期去某景区旅游的人数进行统计，每天旅游的人数统计如下表：
| 日期 | 5月1日 | 5月2日 | 5月3日 | 5月4日 | 5月5日 | 5月6日 | 5月7日 |
| 人数（单位：万） | 1.2 | 2 | 2.5 | 2 | 1.2 | 2 | 0.6 |
其中众数和中位数分别是 （ ）
A．1.2，2 B．2，2.5 C．2，2 D．1.2，2.5
7、在△ABC中，∠C＝90°，如果AB＝2，BC＝1，那么sinA的值是( ).
(A)
(B) 
(C) 
(D) 
8、如图2，A、B是⊙O上的两点，AC是⊙O的切线，∠B＝70°，则∠BAC等于（ ）。
(A) 70° (B) 35° (C) 30° (D) 20°
9、小红、小明、小芳在一起做游戏时，需要确定游戏的先后顺序.他们约定用“剪子、包袱、锤子”的方式确定.问在一个回合中三个人都出包袱的概率是（ ）
（A）
（B）
（C）
（D）
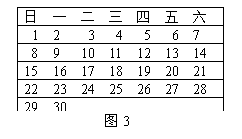
10、如图3，给出的是2007年4月份的日历，任意圈出一竖列上相邻的三个数，请运用方程的思想来研究，你发现这三个数的和不可能是（ ）
（A）27 （B）40 （C）54 （D）72
二、填空题（本题有5小题，每题3分，共15分．）
11、不等式组
的解集是
。
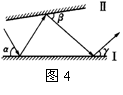
12、光线以如图4所示的角度α照射到平面镜Ⅰ上，然后在平面镜Ⅰ、Ⅱ之间来回反射，已知∠α＝60°，∠β＝50°，∠γ＝ 度。
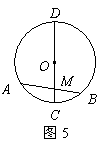13、如图5,⊙O直径CD与弦AB（非直径）交于点M，添加一个条件：______，就可得到点M是AB的中点。
14、一个函数具有下列性质：①它的图象不经过第三象限；②图象经过点（－1，1）；③当
时函数值
随自变量x增大而增大.试写出一个满足上述三条性质的函数的解析式
。
15、“抛出的篮球会下落”，这个事件是 事件（填“确定”或“不确定”）
三、解答题（每小题6分，共36分）
16、计算：
°
解：原式＝
17、有这样一道题：“计算：
的值，其中x＝2007．”甲同学把“x＝2007”错抄成“x＝2070”，但他的计算结果也是正确的．你说这是怎么回事？
解：
18、解方程：解方程：
解：
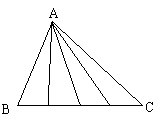
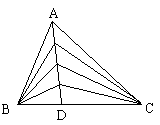
19、如图6，有一块三角形的地，现要平均分给四农户种植（即四等分三角形面积）.请你在图上作出分法.（不写作法，保留作图痕迹）
 |
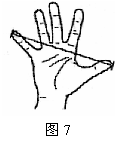
20、如图7，大拇指与小拇指尽量张开时，两指尖的距离称为指距. 某项研究表明，一般情况下人的身高h是指距d的一次函数. 下表是测得的指距与身高的一组数据：
| 指距d(cm) | 20 | 21 | 22 | 23 |
| 身高h(cm) | 160 | 169 | 178 | 187 |
（1）求出h与d之间的函数关系式（不要求写出自变量d的取值范围）；（3分）
（2）某人身高为196cm，一般情况下他的指距应是多少？（2分）
解：
21、中央电视台“幸运 52”栏目中的“百宝箱”互动环节，是一种竞猜游戏，游戏规则如下：在20个商标牌中，有5个商标牌的背面注明一定的奖金额，其余商标牌的背面是一张哭脸，若翻到哭脸，就不得奖，参与这个游戏的观众有三次翻牌机会（翻过的牌不能再翻）.某观众前两次翻牌均获得若干奖金，那么他第三次翻牌获奖的概率是多少？
解：
四．证明题（8分）
22、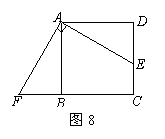
已知：如图8，点E是正方形ABCD的边CD上一点，点F是CB的延长线上一点，且EA⊥AF.
求证：DE=BF.
证明：
五、应用题（本题9分）
23、“五一”期间，某商场搞优惠促销，决定由顾客抽奖确定折扣．某顾客购买甲、乙两种商品，分别抽到七折（按售价的70％销售）和九折（按售价的90％销售），共付款386元，这两种商品原销售价之和为500元．问：这两种商品的原销售价分别为多少元？
解：
六、图表阅读分析题（本题10分）
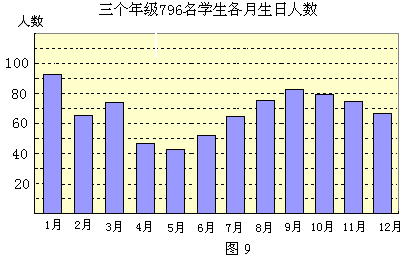
24、2007年，某校三个年级的初中在校学生共796名，学生的出生月份统计如下，根据图9中数据回答以下问题：
（1）出生人数多于60人的月份有哪些？
解：
（2）出生人数最多的是几月？
解：
（3）在这些学生中至少有两人生日在10月5日是不可能的，还是可能的，还是必然的？
解：
（4）如果你随机地遇到这些学生中的一位，那么这位学生生日在哪一个月的概率最小？
解：
七、综合题（本题12分）
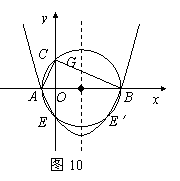25、如图10，在Rt△ABC中,∠ACB=90°,BC>AC,以斜边AB所在直线为x轴,以斜边AB上的高所在直线为y轴,建立直角坐标系,若OA2+OB2=17,且线段OA、OB的长度是关于x的一元二次方程x2-mx+2(m-3)=0的两个根.
（1）求C点的坐标；
（2）以斜边AB为直径作圆与y轴交于另一点E，求过A、B、E三点的抛物线的解析式，并画出此抛物线的草图；
（3）在抛物线上是否存在点P，使△ABP与△ABC全等？若存在，求出符合条件的P点的坐标；若不存在，说明理由.
参考答案
一、选择题（本题有10小题，每题3分，共30分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | B | B | C | A | C | A | D | D | B |
二、填空题（本题有5小题，每题3分，共15分）
| 题号 | 11 | 12 | 13 | 14 | 15 |
| 答案 | 2<x<3 | 40 | CD⊥AB或 弧AC＝弧BC 或弧AD＝弧BD |
| 确定 |
等（写一个即可）三、解答题
16、原式=3－2＋1－1＝1
17、∵
=
=
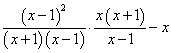
=0
只要
的取值使这个代数式有意义，其值就为0．
∴x＝2007错抄成x=2070不影响结果，都为0 。
18、.解：去分母,得
19、不惟一
①BC任意四等分 ②任意的AD四等分 ③各边中点连结
 | |||||
 | |||||
 | |||||
20、（1）设一次函数的解析式为：y＝kx＋b，依题意，得：
解得：
所以，h与d之间的函数关系式为：h＝9d－20。
（2）当h＝196cm时，196＝9d－20，
解得：d＝24
答：若某人身高为196cm，一般情况下他的指距应是24cm。
21、20个商标中2个已翻出，还剩18张，18张中还有3张有奖的，
所以中奖的概率为：
。
四．证明题
22、∵四边形ABCD是正方形，∴AB=AD，∠BAD=∠ADE=∠ABF=90°
∵EA⊥AF，∴∠BAF+∠BAE=∠BAE+∠DAE=90°，∴∠BAF=∠DAE，
∴Rt△ABF≌Rt△ADE，∴DE=BF.
五．应用题
23、设甲、乙两种商品的原销售价分别为x，y元，根据题意，得：
，解得：
答：甲、乙两种商品的原销售价分别为320元,180元。
六．图表阅读分析题
24、（1）1月份、2月份、3月份、7月份、8月份、9月份、10月份、11月份、12月份；
（2）1月；
（3）可能的； （4）5份月份。
七．综合探究题
25、解：（1）∵线段OA、OB的长度是关于x的一元二次方程x2－mx+2(m－3)=0的两个根，
∴
又 ∵OA2+OB2=17，
∴（OA+OB）2－2·OA·OB=17.（3）
∴把（1）（2）代入（3），得m2－4(m－3)=17.
∴m2－4m－5=0.， 解得m=-1或m=5.
又知OA+OB=m>0，∴m=－1应舍去.
∴当m=5时，得方程x2－5x+4=0.
解之，得x=1或x=4.
∵BC>AC, ∴OB>OA.
∴OA=1，OB=4.
在Rt△ABC中，∠ACB=90°，CO⊥AB，
∴OC2=OA·OB=1×4=4.
∴OC=2， ∴ C（0，2）.
（2）∵OA=1，OB=4，C、E两点关于x轴对称，
∴A(－1,0),B(4,0),E(0,－2).
设经过A、B、E三点的抛物线的解析式为y=ax2+bx+c,则
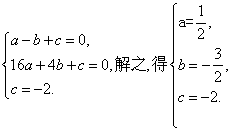
∴所求抛物线解析式为
（3）存在.∵点E是抛物线与圆的交点，
∴Rt△ACB≌△AEB.
∴E（0，-2）符合条件.
∵圆心的坐标（
，0）在抛物线的对称轴上，
∴这个圆和这条抛物线均关于抛物线的对称轴对称.
∴点E关于抛物线对称轴的对称点E′也符合题意.
∴可求得E′（3，-2）.
∴抛物线上存在点P符合题意，它们的坐标是（0，-2）和（3，-2）。