★智闯三关 发挥聪明睿智,关公怎比我强
核心知识----基础关
1.如图,小亮用六块形状、大小完全相同的等腰梯形拼成一个四边形,则图中![]() 的度数是( A )
的度数是( A )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
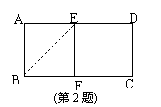
 2.如图,将长方形纸折叠,使A落在BC上F处,折痕为BE,若沿EF剪下来,把所折部分展开是一个正方形,其数学原理是( )
2.如图,将长方形纸折叠,使A落在BC上F处,折痕为BE,若沿EF剪下来,把所折部分展开是一个正方形,其数学原理是( )
A 邻边相等的矩形是正方形;
B 对角线相等的菱形是正方形;
C 正方形被对角线分成两个全等的等腰三角形;
 D 正方形是轴对称图形。
D 正方形是轴对称图形。
 3.如图7,
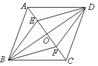
3.如图7,![]() 是菱形
是菱形![]() 的对角线
的对角线![]() 的交点,
的交点,![]() 分别是
分别是![]() 的中点.下列结论:①
的中点.下列结论:①![]() ;②四边形
;②四边形![]() 是中心对称图形;③
是中心对称图形;③![]() 是轴对称图形;④
是轴对称图形;④![]() .其中错误的结论有 .
.其中错误的结论有 .
A.1个 B.2个
|
 .
.

6.如图,矩形草坪![]() 中,
中, ![]() .现需要修一条由两个扇环构成的便道
.现需要修一条由两个扇环构成的便道![]() ,扇环的圆心分别是
,扇环的圆心分别是![]() .若便道的宽为
.若便道的宽为![]() ,则这条便道的面积大约是( C )(精确到
,则这条便道的面积大约是( C )(精确到![]() ).
).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.如图,矩形![]() 的对角线
的对角线![]() 和
和![]() 相交于点
相交于点![]() ,过点
,过点![]() 的直线分别交
的直线分别交![]() 和
和![]() 于点
于点![]() ,
,![]() ,则图中阴影部分的面积为 3 .
,则图中阴影部分的面积为 3 .
 | |||
| |||
8.将一个无盖正方体纸盒展开(如图①),沿虚线剪开,用得到的5张纸片(其中4张是全等的直角三角形纸片)拼成一个正方形(如图②).则所剪得的直角三角形较短的与较长的直角边的比是 1:2 .
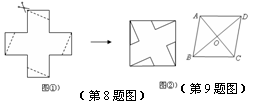 |
9.如图,菱形![]() 的对角线
的对角线![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,则菱形
,则菱形![]() 的面积是
的面积是 ![]() .
.
|
 10.如图,将矩形纸片
10.如图,将矩形纸片核心能力-----技能关
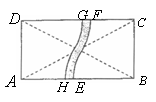
11.如图1,2所示,将一张长方形的纸片对折两次后,沿图3中的虚线![]() 剪下,将
剪下,将![]() 完全展开.
完全展开.
(1)画出展开图形,判断其形状,并证明你的结论;
(2)若按上述步骤操作,展开图形是正方形时,请写出![]() 应满足的条件.
应满足的条件.
|
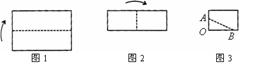
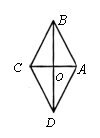 解:(1)展开图如图所示,它是菱形.(展开图只要求画出示意图即可.)
解:(1)展开图如图所示,它是菱形.(展开图只要求画出示意图即可.)
证明:由操作过程可知![]() ,
, ![]() ,
,![]() 四边形
四边形![]() 是平行四边形.又
是平行四边形.又![]() ,即
,即![]() ,
,![]() 四边形
四边形![]() 是菱形.
是菱形.
(2)![]() 中,
中,![]() (或
(或![]() 或
或![]() ).
).
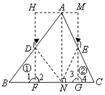
12.)任意剪一个三角形纸片,如图中的![]() ,不妨设它的一个锐角为
,不妨设它的一个锐角为![]() ,首先利用对折的方法得到高
,首先利用对折的方法得到高![]() .然后按图中所示的方法分别将含有
.然后按图中所示的方法分别将含有![]() 的部分向里折,找出
的部分向里折,找出![]() 的中点
的中点![]() ,同时得到两条折痕
,同时得到两条折痕![]() ,分别沿折痕
,分别沿折痕![]() 剪下图中的三角形①,②,并按图中箭头所指的方向分别旋转
剪下图中的三角形①,②,并按图中箭头所指的方向分别旋转![]() .
.
(1)你能拼成一个什么样的四边形?并说明你的理由;
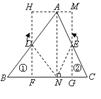 (2)请你利用这个图形,证明三角形的面积公式:
(2)请你利用这个图形,证明三角形的面积公式:![]() .
.
|
(1)答:拼出的四边形![]() 是矩形.
是矩形.
 证明:由题意,得
证明:由题意,得![]()
![]()
![]()
![]()
![]()
|
(2)由题意,得
![]()
![]()
![]() ,
,![]()
![]()
即:三角形的面积![]() .
.
13.如图,在梯形![]() 中,
中,![]() ,过对角线
,过对角线![]() 的中点
的中点![]() 作
作![]() ,分别交边
,分别交边![]() 于点
于点![]() ,连接
,连接![]() .
.
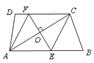 (1)求证:四边形
(1)求证:四边形![]() 是菱形;
是菱形;
|
求四边形![]() 的面积.
的面积.
(1)证明:方法1:![]() ,
,![]() .
.
在![]() 和
和![]() 中,
中,
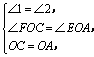
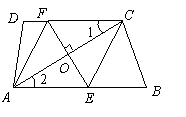
![]() .
.![]() ,
,
又![]() ,
,![]() 四边形
四边形![]() 是平行四边形.
是平行四边形.
![]() ,
,![]() 四边形
四边形![]() 是菱形.
是菱形.
方法2:证![]() 同方法1,
同方法1,
![]() ,
,![]() ,
,![]() 四边形
四边形![]() 是平行四边形.
是平行四边形. ![]() ,
,
![]() 是
是![]() 的垂直平分线,
的垂直平分线,![]() ,
,
![]() 四边形
四边形![]() 是菱形.
是菱形.
(2)解:![]() 四边形
四边形![]() 是菱形,
是菱形,![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
![]() .
.
![]() .
.
核心精神---创新关
15.
16.(2006郴州)如图1,矩形纸片![]() 的边长分别为
的边长分别为![]() .将纸片任意翻折(如图2),折痕为
.将纸片任意翻折(如图2),折痕为![]() .(
.(![]() 在
在![]() 上),使顶点
上),使顶点![]() 落在四边形
落在四边形![]() 内一点
内一点![]() ,
,![]() 的延长线交直线
的延长线交直线![]() 于
于![]() ,再将纸片的另一部分翻折,使
,再将纸片的另一部分翻折,使![]() 落在直线
落在直线![]() 上一点
上一点![]() ,且
,且![]() 所在直线与
所在直线与![]() 所在直线重合(如图3)折痕为
所在直线重合(如图3)折痕为![]() .
.
(1)猜想两折痕![]() 之间的位置关系,并加以证明.
之间的位置关系,并加以证明.
(2)若![]() 的角度在每次翻折的过程中保持不变,则每次翻折后,两折痕
的角度在每次翻折的过程中保持不变,则每次翻折后,两折痕![]() 间的距离有何变化?请说明理由.
间的距离有何变化?请说明理由.
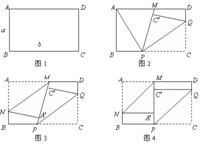 (3)若
(3)若![]() 的角度在每次翻折的过程中都为
的角度在每次翻折的过程中都为![]() (如图4),每次翻折后,非重叠部分的四边形
(如图4),每次翻折后,非重叠部分的四边形![]() ,及四边形
,及四边形![]() 的周长与
的周长与![]() 有何关系,为什么?
有何关系,为什么?
|
解:(1)![]() .
.
因为四边形![]() 是矩形,所以
是矩形,所以![]() ,且
,且![]() 在
在![]() 直线上,则有
直线上,则有![]()
∴![]() ,由翻折可得:
,由翻折可得:![]() ,
,![]() ,
,
∴![]() ,故
,故![]() .
.
(2)两折痕![]() 间的距离不变
间的距离不变
过![]() 作
作![]() ,则
,则![]() ,
,
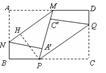 因为
因为![]() 的角度不变,所以
的角度不变,所以![]() 的角度也不变,则所有的
的角度也不变,则所有的![]() 都是平行的.
都是平行的.
又因为![]() ,所以所有的
,所以所有的![]() 都是相等的
都是相等的
又因为![]() ,
,
故![]() 的长不变.
的长不变.
(3)当![]() 时,四边形
时,四边形![]() 是正方形,
是正方形,
四边形![]() 是矩形.因为
是矩形.因为![]() ,
,![]() ,所以矩形
,所以矩形![]() 的周长为
的周长为![]() .
.
同理可得矩形![]() 的周长为
的周长为![]() ,所以两个四边形的周长都为
,所以两个四边形的周长都为![]() ,与
,与![]() 无关.
无关.