第二节 一次函数
【回顾与思考】
一次函数
【例题经典】
理解一次函数的概念和性质
例1 若一次函数y=2x
+m-2的图象经过第一、第二、三象限，求m的值．
【分析】这是一道一次函数概念和性质的综合题．一次函数的一般式为y=kx+b（k≠0）．首先要考虑m2-2m-2=1．函数图象经过第一、二、三象限的条件是k>0,b>0，而k=2，只需考虑m-2>0．由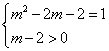
便可求出m的值．
用待定系数法确定一次函数表达式及其应用
例2 （2006年济宁市）鞋子的“鞋码”和鞋长（cm）存在一种换算关系，下表是几组“鞋码”与鞋长的对应数值：
| 鞋长 | 16 | 19 | 24 | 27 |
| 鞋码 | 22 | 28 | 38 | 44 |
（1）分析上表，“鞋码”与鞋长之间的关系符合你学过的哪种函数？
（2）设鞋长为x，“鞋码”为y，求y与x之间的函数关系式；
（3）如果你需要的鞋长为26cm，那么应该买多大码的鞋？
【评析】本题是以生活实际为背景的考题．题目提供了一个与现实生活密切联系的问题情境，以考查学生对有关知识的理解和应用所学知识解决问题的能力，同时为学生构思留下了空间．
建立函数模型解决实际问题
例3 （2006年南京市）某块试验田里的农作物每天的需水量y（千克）与生长时间x（天）之间的关系如折线图所示．这些农作物在第10天、第30天的需水量分别为2000千克、3000千克，在第40天后每天的需水量比前一天增加100千克．
（1）分别求出x≤40和x≥40时y与x之间的关系式；
（2）如果这些农作物每天的需水量大于或等于4000千克时，需要进行人工灌溉，那么应从第几天开始进行人工灌溉？
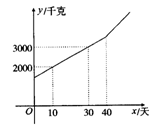
【评析】本题提供了一个与生产实践密切联系的问题情境，要求学生能够从已知条件和函数图象中获取有价值的信息，判断函数类型．建立函数关系．为学生解决实际问题留下了思维空间．
【考点精练】
基础训练
1．下列各点中，在函数y=2x-7的图象上的是（ ）
A．（2，3） B．（3，1） C．（0，-7） D．（-1，9）
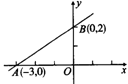
2．如图，一次函数y=kx+b的图象经过A、B两点，则kx+b>0的解集是（ ）
A．x>0 B．x>2 C．x>-3 D．-3<x<2
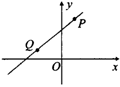
(第2题) (第4题) (第7题)
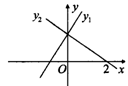
3．已知两个一次函数y1=-
x-4和y2=-
x+的图象重合，则一次函数y=ax+b的图象所经过的象限为（ ）
A．第一、二、三象限 B．第二、三、四象限
C．第一、三、四象限 D．第一、二、四象限
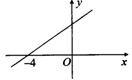
4．如图，直线y=kx+b与x轴交于点（-4，0），则y>0时，x的取值范围是（ ）
A．x>-4 B．x>0 C．x<-4 D．x<0
5．（2005年杭州市）已知一次函数y=kx-k，若y随x的增大而减小，则该函数的图像经过（ ）
A．第一、二、三象限 B．第一、二、四象限
C．第二、三、四象限 D．第一、三、四象限
6．点P1（x1，y1），点P2（x2，y2）是一次函数y=-4x+3图象上的两个点，且x1<x2，则y1与y2的大小关系是（ ）
A．y1>y2 B．y1>y2>0 C．y1<y2 D．y1=y2
7．（2006年绍兴市）如图，一次函数y=x+5的图象经过点P（a，b）和点Q（c，d），则a（c-d）-b（c-d）的值为________．
8．（2006年贵阳市）函数y1=x+1与y2=ax+b的图象如图所示，这两个函数的交点在y轴上，那么y1、y2的值都大于零的x的取值范围是_______．
9．（2006年重庆市）如图，已知函数y=ax+b和y=kx的图象交于点P， 则根据图象可得，关于
的二元一次方程组的解是________．
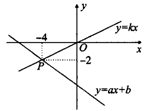
(第8题) (第9题)
10．（2006年安徽省）一次函数的图象过点（-1，0），且函数值随着自变量的增大而减小，写出一个符合这个条件的一次函数的解析式：___________．
能力提升
11．（2006年宿迁市）经过点（2，0）且与坐标轴围成的三角形面积为2的直线解析式是_________．
12．（2006年德阳市）地表以下岩层的温度t（℃）随着所处的深度h（千米）的变化而变化．t与h之间在一定范围内近似地成一次函数关系．
（1）根据下表，求t（℃）与h（千米）之间的函数关系式；
（2）求当岩层温度达到1770℃时，岩层所处的深度为多少千米？
| 温度t（℃） | … | 90 | 160 | 300 | … |
| 深度h（km） | … | 2 | 4 | 8 | … |
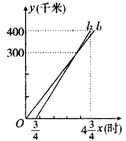
13．（2006年陕西省）甲、乙两车从A地出发，沿同一条高速公路行驶至距A地400千米的B地．L1、L2分别表示甲、乙两车行驶路程y（千米）与时间x（时）之间的关系（如图所示），根据图象提供的信息，解答下列问题：
（1）求L2的函数表达式（不要求写出x的取值范围）；
（2）甲、乙两车哪一辆先到达B地？该车比另一辆车早多长时间到达B地？
14．（2006年伊春市）某工厂用一种自动控制加工机制作一批工件，该机器运行过程分为加油过程和加工过程；加工过程中，当油箱中油量为10升时，机器自动停止加工进入加油过程，将油箱加满后继续加工，如此往复．已知机器需运行185分钟才能将这批工件加工完．下图是油箱中油量y（升）与机器运行时间x（分）之间的函数图象．根据图象回答下列问题：
（1）求在第一个加工过程中，油箱中油量y（升）与机器运行时间x（分）之间的函数关系式（不必写出自变量x的取值范围）；
（2）机器运行多少分钟时，第一个加工过程停止？
（3）加工完这批工件，机器耗油多少升？
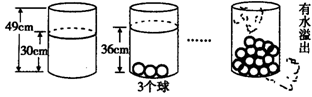
15．（2006年吉林省）小明受《乌鸦喝水》故事的启发，利用量筒和体积相同的小球进行了如下操作：
请根据图中给出的信息，解答下列问题：
（1）放入一个小球量筒中水面升高_______cm；
（2）求放入小球后量筒中水面的高度y（cm）与小球个数x（个）之间的一次函数关系式（不要求写出自变量的取值范围）；
（3）量筒中至少放入几个小球时有水溢出？
应用与探究
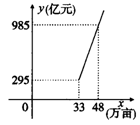
16．（2006年宁波市）宁波市土地利用现状通过国土资源部验收，我市在节约集约用地方面已走在全国前列，1996～2004年，市区建设用地总量从33万亩增加到48万亩，相应的年GDP从295亿元增加到985亿元．宁波市区年GDP为y（亿元）与建设用地总量x（万亩）之间存在着如图所示的一次函数关系．
（1）求y关于x的函数关系式．
（2）据调查2005年市区建设用地比2004年增加4万亩，如果这些土地按以上函数关系式开发使用，那么2005年市区可以新增GDP多少亿元？
（3）按以上函数关系式，我市年GDP每增加1亿元，需增建设用地多少万亩？（精确到0.001万亩）
答案:
例题经典
例1：m=3 例2：（1）一次函数，
（2）设y=kx+b，则由题意，得
，
∴y=2x-10，（3）x=26时，y=2×26-10=42．
答：应该买42码的鞋．
例3：解：（1）当x≤40时，设y=kx+b．
根据题意，得
，
∴当x≤40时，y与x之间的关系式是y=50x+1500，
∴当x=40时，y=50×40+1500=3500，
当x≥40时，根据题意得，y=100（x-40）+3500，即y=100x-500．
∴当x≥40时，y与x之间的关系式是y=100x-500．
（2）当y≥4000时，y与x之间的关系式是y=100x-500，
解不等式100x-50≥4000，得x≥45，
∴应从第45天开始进行人工灌溉．
考点精练
1．C 2．C 3．D 4．A 5．B 6．A 7．25 8．1<x<2
9．
10．答案不唯一．例如：y=-x-1 11．y=x-2或y=-x+2
12．（1）t与h的函数关系式为t=35h+20．
（2）当t=1770时，有1770=35h+20，解得：h=50千米．
13．解：（1）设L2的函数表达式是y=k2x+b，则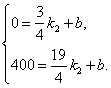
解之，得k2=100，b=-75，∴L2的函数表达式为y=100x-75．
（2）乙车先到达B地，∵300=100x-75，∴x=
．
设L1的函数表达式是y=k1x，∵图象过点（，300），
∴k1=80．即y=80x．当y=400时，400=80x，
∴x=5，∴5-
=
（小时），
∴乙车比甲车早小时到达B地．
14．解：（1）设所求函数关系式为y=kx+b，由图象可知过（10，100），（30，80）两点，得
，∴y=-x+110．
（2）当y=10时，-x+110=10，x=100，机器运行100分钟时，第一个加过程停止．
（3）第一加工过程停止后再加满油只需9分钟，加工完这批工件，机器耗油166升．
15．解：（1）2，
（2）设y=kx+b，把（0，30），（3，36）代入得：
，即y=2x+30．
（3）由2x+30>49，得x>9．5，即至少放入10个小球时有水溢出．
16．解：（1）设函数关系式为y=kx+b，由题意得
，
解得k=46，b=-1223，∴该函数关系式为y=46x-1223．
（2）由（1）知2005年的年GDP为46×（48+4）-1223=1169（亿元），
∵1169-985=184（亿元），∴2005年市区相应可以新增加GDP184亿元．
（3）设连续两个建设用地总量分别为x1万亩和x2万亩，
相应年GDP分别为y1亿元和y2亿元，满足y2-y1=1，则
y1=46x1-1223 ③ y2=46x2-1223 ④，
④-③得y2-y1=46（x2-x1），即46（x2-x1）=1，
∴x2-x1=
≈0.022（万亩），
即年GDP每增加1亿元，需增加建设用地约0.022万亩．