第四节 二次函数
【回顾与思考】
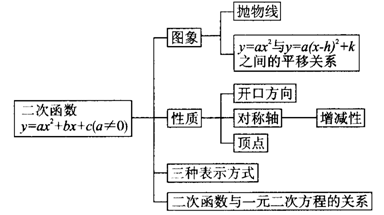
【例题经典】
由抛物线的位置确定系数的符号
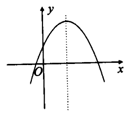
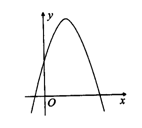
例1 （1）二次函数y=ax2+bx+c的图像如图1，则点M（b，
）在（ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
（2）（2005年武汉市）已知二次函数y=ax2+bx+c（a≠0）的图象如图2所示，则下列结论：①a、b同号；②当x=1和x=3时，函数值相等；③4a+b=0；④当y=-2时，x的值只能取0.其中正确的个数是（ ）
A．1个 B．2个 C．3个 D．4个
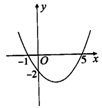
(1) (2)
【点评】弄清抛物线的位置与系数a，b，c之间的关系，是解决问题的关键．
会用待定系数法求二次函数解析式
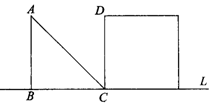
例2 （2006年烟台市）如图（单位：m），等腰三角形ABC以2米/秒的速度沿直线L向正方形移动，直到AB与CD重合．设x秒时，三角形与正方形重叠部分的面积为ym2．
（1）写出y与x的关系式；
（2）当x=2，3.5时，y分别是多少？
（3）当重叠部分的面积是正方形面积的一半时，三角形移动了多长时间？
求抛物线顶点坐标、对称轴.
例3 （2005年天津市）已知抛物线y=
x2+x-
．
（1）用配方法求它的顶点坐标和对称轴．
（2）若该抛物线与x轴的两个交点为A、B，求线段AB的长．
【点评】本题（1）是对二次函数的“基本方法”的考查，第（2）问主要考查二次函数与一元二次方程的关系．
【考点精练】
基础训练
1．二次函数y=x2的图象向右平移3个单位，得到新的图象的函数表达式是（ ）
A．y=x2+3 B．y=x2-3 C．y=（x+3）2 D．y=（x-3）2
2．二次函数y=-（x-1）2+3图像的顶点坐标是（ ）
A．（-1，3） B．（1，3） C．（-1，-3） D．（1，-3）
3．二次函数y=x2+x-6的图象与x轴交点的横坐标是（ ）
A．2和-3 B．-2和3 C．2和3 D．-2和-3
4．二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：①a>0；②c>0；③b2-4ac>0，其中正确的个数是（ ）
A．0个 B．1个 C．2个 D．3个
5．（2006年常德市）根据下列表格中二次函数y=ax2+bx+c的自变量x与函数值y的对应值，判断方程ax2+bx+c=0（a≠0，a，b，c为常数）的一个解x的范围是（ ）
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y=ax2+bx+c | -0.03 | -0.01 | 0.02 | 0.04 |
A．6<x<6.17 B．6.17<x<6.18
C．6.18<x<6.19 D．6.19<x<6.20
6．（2006年南充市）二次函数y=ax2+bx+c，b2=ac，且x=0时y=-4则（ ）
A．y最大=-4 B．y最小=-4 C．y最大=-3 D．y最小=3
7．（2006年苏州市）抛物线y=2x2+4x+5的对称轴是x=______．
8．（2006年宿迁市）将抛物线y=x2向左平移4个单位后，再向下平移2个单位，则此时抛物线的解析式是________．
9．（2006年锦州市）已知二次函数的图象开口向上，且顶点在y轴的负半轴上，请你写出一个满足条件的二次函数的表达式________．
10．（2006年长春市）函数y=x2+bx-c的图象经过点（1，2），则b-c的值为______．
能力提升
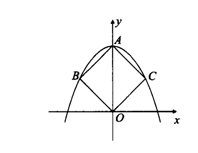11．如图，在平面直角坐标系中，二次函数y=ax2+c（a≠0）的图象过正方形ABOC的三个顶点A，B，C，则ac的值是________．
12．观察下面的表格：
| x | 0 | 1 | 2 |
| ax2 | 2 | ||
| ax2+bx+c | 4 | 6 |
（1）求a，b，c的值，并在表格内的空格中填上正确的数；
（2）求二次函数y=ax2+bx+c图象的顶点坐标与对称轴．
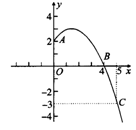
13．（2006年南通市）已知抛物线y=ax2+bx+c经过A，B，C三点，当x≥0时，其图象如图所示．
（1）求抛物线的解析式，写出抛物线的顶点坐标；
（2）画出抛物线y=ax2+bx+c当x<0时的图象；
（3）利用抛物线y=ax2+bx+c，写出x为何值时，y>0．
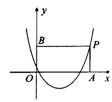
14．（2006年长春市）如图，P为抛物线y=
x2-
x+
上对称轴右侧的一点，且点P在x轴上方，过点P作PA垂直x轴于点A，PB垂直y轴于点B，得到矩形PAOB．若AP=1，求矩形PAOB的面积．
15．（2006年莆田市）枇杷是莆田名果之一．某果园有100棵枇杷树，每棵平均产量为40千克．现准备多种一些枇杷树以提高产量，但是如果多种树，那么树之间的距离和每一棵树接受的阳光就会减少．根据实践经验，每多种一棵树，投产后果园中所有的枇杷树平均每棵就会减少产量0.25千克．问：增种多少棵枇杷树，投产后可以使果园枇杷的总产量最多？最多总产量是多少千克？[注：抛物线y=ax2+bx+c的顶点坐标是（-
，
）]
应用与探究
16．（2006年常州市）在平面直角坐标系中，已知二次函数y=a（x-1）2+k的图像与x轴相交于点A、B，顶点为C，点D在这个二次函数图像的对称轴上，若四边形ABCD是一个边长为2且有一个内角为60°的菱形，求此二次函数的表达式．
答案:
例题经典
例1：（1）D （2）B 例2：（1）y=2x2，（2）8；24.5；（3）5秒．
例3：（1）顶点（-1，-3），对称轴x=-1，（2）2
考点精练
1．D 2．B 3．A 4．C 5．C 6．C 7．x=-1 8．y=（x+4）2-2（y=x2+8x+14）
9．答案不唯一，符合要求即可．如：y=x2-2 10．1 11．-2
12．（1）a=2，b=-3，c=4，0，8，3 （2）顶点（，
）对称轴是直线x=
13．（1）y=-x2+x+2，顶点坐标（，
） （2）略，（3）当-1<x<4时，y>0．
14．∵PA⊥x轴，AP=1，∴点P的纵坐标为1．当y=1时，x2-x+=1，
即x2-2x-1=0，解得x1=1+
，x2=1-，
∵抛物线的对称轴为x=1，点P在对称轴的右侧，
∴x=1+，∴矩形PAOB的面积为（1+）个平方单位．
15．设增种x棵时，果园的总产量为y千克，
根据题意得：y=（100+x）（40-0.25x）=4000-25x+40x-0.25x2=-0.25x2+15x+4000，
∵a=-0.25<0，
∴当x=-=-
=30时，y最大，
y最大值==
=4225．
答：当增种30棵枇杷树时，投产后果园总产量最多，达4225千克．
16．解：本题共四种情况，设二次函数的图像的对称轴与x轴相交于点E，
（1）如图①，
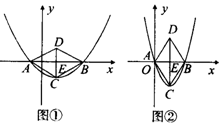
当∠CAD=60°时，因为ABCD为菱形，一边长为2，
所以DE=1，BE=
，所以点B的坐标为（1+，0），点C的坐标为（1，-1），
解得k=-1，a=
，所以y=（x-1）2-1．
（2）如图②，当∠ACB=60°时，由菱形性质知点A的坐标为（0，0），
点C的坐标为（1，），解得k=-，a=，所以y=（x-1）2-，
同理可得：y=-（x-1）2+1=，y=-（x-1）2+，
所以符合条件的二次函数的表达式有：
y=（x-1）2-1，
y=（x-1）2-，
y=-（x-1）2+1，
y=-（x-1）2+．