中考复习系列《图形的认识》
第一课时 点、线、角
初三（ ）班 学号： 姓名：
一、中考知识要点
1、
线段与角
（1）右图，线段有
直线有
射线有 （写两条）
（2）直线公理：经过 点有且仅有一条直线。
（3）线段公理：两点之间 最短。
（4）余角：∠1和∠2互余，则∠1+∠2=
余角的性质： 角或 角的余角相等。
，则
=
（5）补角：∠1和∠2互补，则∠1+∠2=
补角的性质： 角或 角的补角相等。
，则
=
（6）直角等于 度，平角等于 度，周角等于 度。
2、相交线与平行线
（1）同一平面内两条直线的位置关系： 、 。
点到直线的距离：直线外一点到这条直线的
的长度。
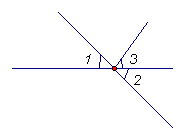
（2）对顶角的性质：对顶角 。
如右图， 与 是对顶角
（3）过直线外一点，有且仅有 条直线与这条直线平行。
推论：如果两条直线都和第三条直线平行，那么这两条直线也互相 。
即a∥b, a∥c,则
（4） 平行线的性质（特征）
两直线 ，同位角 。
两直线 ，内错角 。
两直线 ，同旁内角 。
（5）平行线的判定（识别）
同位角 ，两直线 。
内错角 ，两直线 。
同旁内角 ，两直线 。
3、垂线的性质
（1）过一点有且只有 条直线与已知直线垂直。
（2）直线外一点到直线上的点的距离中， 线段最短。
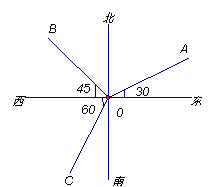
4、方位角
射线OA表示
射线OB表示
射线OC表示
二、中考典型题
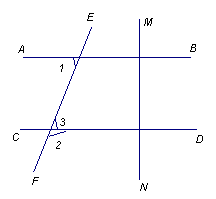
例1、 如图所示，AB⊥MN, CD⊥MN，∠1=70°，
求∠2的度数。
解：∵AB⊥MN, CD⊥MN，
∴AB CD
∴∠1=∠ = ，
又∵∠2+∠3=
∴∠2=
例2、
已知一个锐角的余角比这个锐角的补角的
还少10°，求这个锐角的度数。
解：设这个锐角为x°，则它的余角为： ，它的补角为：
根据题意，列方程
例3、
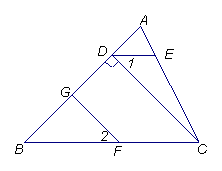如图，已知CD⊥AB于D, DE∥BC, ∠1=∠2，求证：FG⊥AB
分析： 要证FG⊥AB
已知CD⊥AB
即要证FG∥CD
（完成分析图） 即要证
证明：
 |
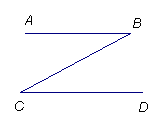习题1、如图，（1）若AB∥CD, 则∠ =∠
（2）若∠B=∠C,则 ∥
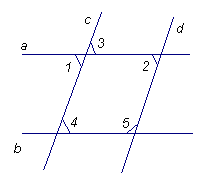
2、如图
（1）若a∥b,则∠ =∠
（ ）
（2）若a∥b, 则∠ =∠
（ ）
（3）若a∥b, 则∠ +∠ =180°（ ）
（4）若c∥d, 则∠ =∠ （ ）
（5）若c∥d, 则∠ =∠ （ ）
（6）若c∥d,则∠ +∠ =180°（ ）
（7）若∠3=∠4，则 ∥ （ ）
（8）若∠1=∠2，则 ∥ （ ）
（9）若∠2+∠5=180°，则 ∥ （ ）
（10）若∠4+∠5=180°，则 ∥ （ ）
（11）若∠1=∠4，则 ∥ （ ）
（12）若∠3=∠2，则 ∥ （ ）
3、度、分、秒的换算
1度= 分= 秒 1秒= 分 1分= 度
14.28°= 度 分 秒； 
=
°
-26°
=
；
=
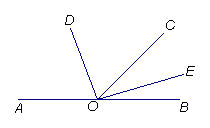4、O是直线AB上一点，OD平分∠AOC,OD
于O, ∠AOD=60°,求∠COE的度数。