提高测试
（一）判断题（每题2分，共10分）
1．过线段外一点画线段的中垂线……………………………………………………（ ）
【提示】线段外一点不一定在线段的中垂线上，所以过线段外一点画线段的垂线，不一定平分这条线段如图PQ⊥AB，垂足为O．但PQ不平分AB．
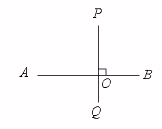
【答案】×．
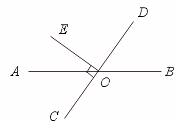
2．如果两个角互为补角，那么它们的角平分线一定互相垂直……………………（ ）
【提示】两个角互为补角时，这两个角可以是邻补角，也可以不是邻补角．当两角互补但不是邻补角时，则它们的角平分线不互相垂直．如图：∠AOB与∠AOC互补，OM平分∠AOC、ON平分∠AOB．显然OM与ON不垂直．
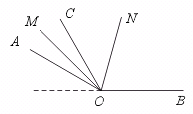
【答案】×．
3．两条直线不平行，同旁内角不互补………………………………………………（ ）
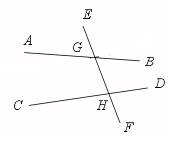
【提示】如图，AB与CD不平行，EF与AB交于点G．与CD交于点H．
过点G作PQ∥CD．
∴ ∠QGF＋∠GHD＝180°．
∵ ∠BGF＜∠QGF，
∴ ∠BGF＋∠GHD＜180°；
又 ∠PGH＋∠GHC＝180°，
∵ ∠AGH＞∠PGH，
∴ ∠AGH＋∠GHC＞180°．
即两直线不平行，同旁内角不互补．
【答案】√．
4．错误地判断一件事情的语句不叫命题……………………………………………（ ）
【提示】判断一件事情的语句叫做命题．错误地判断得到的是假命题．假命题也是命题．
【答案】×．
5．如图，AB∥CD，那么∠B＋∠F＋∠D＝∠E＋∠G…………………………（ ）
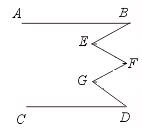
【提示】过点E、F、G分别画EP∥AB，PQ∥AB，GM∥AB．
则AB∥EP∥FQ∥GM∥CD．
∴ ∠B＝∠1，∠3＝∠2，∠4＝∠5，∠D＝∠6．
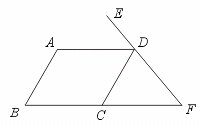
∴ ∠B＋∠3＋∠4＋∠D＝∠1＋∠2＋∠5＋∠6．
即∠B＋∠EFG＋∠D＝∠BEF＋∠FG（D）
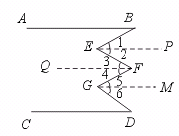
【答案】√．
（二）填空题（每小题2分，共18分）
6．如图，当∠1＝∠ 时，AB∥DC；当∠D＋∠ ＝180°时，AB∥DC；当∠B＝∠ 时，AB∥CD．
【提示】把题中的“AB∥CD”视作条件去找∠1的内错角、∠D的同旁内角和∠B的同位角．即得要填的角．
【答案】4，DAB，5．
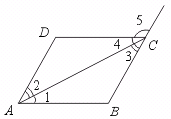
7．如图，AB∥CD，AD∥BC，∠B＝60°，∠EDA＝50°．则∠CDF＝ ．
【提示】由AB∥CD，得∠DCF＝∠B＝60°，
由AD∥BC得∠ADC＝∠DCF＝60°，
∴ ∠ADE＋∠ADC＝50°＋60°＝110°，
∴ ∠CDF＝180°－110°＝70°．
【答案】70°．
8．如图，O是△ABC内一点，OD∥AB，OE∥BC，OF∥AC，∠B＝45°，∠C＝75°，则∠DOE＝ ，∠EOF＝ ，∠FOD＝ ．
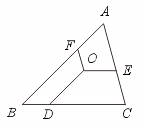
【提示】由OD∥AB，∠B＝45°，得∠ODC＝∠B＝45°．
由OE∥DC，∠DOE＋∠ODC＝180°，∴ ∠DOE＝180°－45°＝135°．
同理可求∠EOF＝105°．由周角的定义可求∠FOD＝120°．
【答案】135°，105°，120°．
9．两个角的两边分别平行，其中一个角比另一个角的3倍少20°．则这两个角的度数分别是 ．
【提示】如果一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补．
设一个角为x度．则另一个角为（3x－20）度．
依据上面的性质得，
3x－20＝x，或3x－20＋x＝180°．
∴ x＝10，或x＝50．
当x＝50时，3x－20＝3×50－20＝130．
【答案】10°、10°或50°、130°．
【点评】通过列方程（或方程组）解题是几何计算常用的方法．
10．如图，AB∥EF∥CD，EG平分∠BEF，∠B＋∠BED＋∠D＝192°，
∠B－∠D＝24°，则∠GEF＝ ．
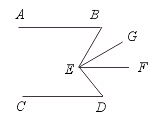
【提示】由AB∥EF∥CD，可知∠BED＝∠B＋∠D．
已知∠B＋∠BED＋∠D＝192°．
∴ 2∠B＋2∠D＝192°，∠B＋∠D＝96°．
又 ∠B－∠D＝24°．
于是可得关于∠B、∠D的方程组
解得 ∠B＝60°．
由AB∥EF知∠BEF＝∠B＝60°．
因为EG平分∠BEF，所以∠GEF＝
∠BEF＝30°．
【答案】30°．
11．如图，AD∥BC，点O在AD上，BO、CO分别平分∠ABC、∠DCB，若
∠A＋∠D＝m°．则∠BOC＝______．
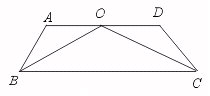
【提示】由AD∥BC，BO平分∠ABC，可知∠AOB＝∠CBO＝∠ABC．
同理∠DOC＝∠BCO＝∠DCB．
∵ AD∥BC，
∴ ∠A＋∠ABC＝180°，∠D＋∠DCB＝180°，
∴ ∠A＋∠D＋∠ABC＋∠DCB＝360°．
∵ ∠A＋∠D＝m°，∴ ∠ABC＋∠DCB＝360°－m°．
∴ ∠AOB＋∠DOC＝（∠ABC＋∠DCB）＝（360°－m°）＝180°－m°．
∴ ∠BOC＝180°－（∠AOB＋∠DOC）＝180°－（180°－m°）＝m°．
【答案】m°．
12．有一条直的等宽纸带，按图（1）折叠时，纸带重叠部分中的∠a＝度．
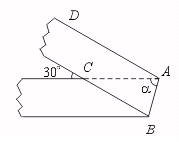
图（1）
【提示】裁一张等宽纸带按图示折叠，体会一下题目的含义．将等宽纸带展平，便得图（2）．由此图可知∠DAC＝30°．AB是∠C′AC的平分线．∴ ∠a＝75°．
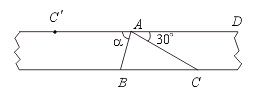
图（2）
【答案】75°．
【点评】解类似具有操作性的实际问题时，不妨动手做一做，从中感受一下题目的意义，进而将实际问题转化成数学问题．用数学知识解决实际问题．这样做不仅能培养我们抽象思维和空间想象能力，而且能提高我们解决实际问题的能力．
13．把命题“在同一平面内垂直于同一直线的两直线互相平行”写成“如果…那么…”的形式是：如果______________，那么_____________．
【答案】在同一平面内两条直线垂直于同一条直线，这两条直线互相平行．
14．如图，在长方体中，与面BCC′B′平行的面是面；与面BCC′B′垂直的面是，与棱A′A平行的面有，与棱A′A垂直的面有．
【答案】面ADD′A；面ABB′A′，面ABCD，面A′B′C′D′，面DCC′D′；
面DCC′D′，面BCC′B′；面ABCD，面A′B′C′D′．
（三）选择题（每小题3分，共21分）
15．如图，已知直线AB与CD相交于点O，OE⊥CD．垂足为O，则图中∠AOE和
∠DOB的关系是……………………………………………………………………（ ）
（A）同位角 （B）对顶角 （C）互为补角 （D）互为余角
【提示】由OE⊥CD，知：∠AOE与∠AOC互余．∠AOC与∠BOD是对顶角．所以∠AOE与∠DOB互为余角．
【答案】D．
16．如图，CD⊥AB，垂足为D，AC⊥BC，垂足为C．图中线段的长能表示点到直线（或线段）距离的线段有…………………………………………………………（ ）
（A）1条 （B）3条 （C）5条 （D）7条
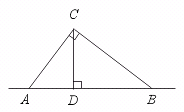
【提示】CD的长表示点C到AB的距离；AC的长表示点A到BC的距离；BC的长表示点B到AC的距离；AD的长表示点A到CD的距离，BD的长表示点B到CD的距离．共5条．
【答案】C．
17．若AO⊥BO，垂足为O，∠AOC︰∠AOB＝2︰9，则∠BOC的度数等于……（ ）
（A）20° （B）70° （C）110° （D）70°或110°
【提示】OC可在∠AOB内部，也可在∠AOB外部，如图可示，故有两解．
设∠AOC＝2x°，则∠AOB＝9x°．
∵ AO⊥BO，
∴ ∠AOB＝90°．
∵ 9x＝90°，x＝10°，∠AOC＝2x＝20°．
（1）∠BOC＝∠AOB－∠AOC＝90°－20°＝70°；
（2）∠BOC＝∠AOB＋∠AOC＝90°＋20°＝110°．
【答案】D．
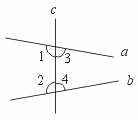
18．下列命题中，真命题是……………………………………………………………（ ）
（A）同位角相等工 （B）同旁内角相等，两直线平行
（C）同旁内角互补 （D）同一平面内，平行于同一直线的两直线平行
【提示】两直线不平行，则同位角不相等，同旁内角不互补，所以A、C错误，B也不一定成立．如图所示直线a、b被直线c所截．∠1＝∠2，∠3＝∠4．显然a与b不平行．
【答案】D．
19．直线AB∥CD，且与EF、GH相交成如图可示的图形，则共得同旁内角…（ ）
（A）4对 （B）8对 （C）12对 （D）16对
【提示】该图可分离出四个基本图形，如图所示．
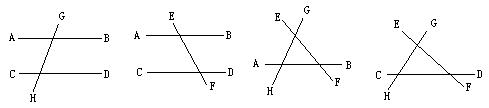
第三条直线截两平行线，此时图形呈“
”型，有同旁内角两对；
第三条直线截两相交线，此时图形呈“
”型，有同旁内角六对．
故图中共有同旁内角2×2＋6×2＝16（对）．
【答案】D．
20．如图，AD∥EF∥BC，且EG∥AC．那么图中与∠1相等的角（不包括∠1）的个数是………………………………………………………………………………（ ）
（A）2 （B）4 （C）5 （D）6
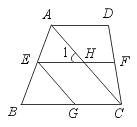
【提示】由AD∥EF∥BC，且EG∥AC可得：
∠1＝∠DAH＝∠FHC＝∠HCG＝∠EGB＝∠GEH除∠1共5个．
【答案】C．
21．某人从A点出发向北偏东60°方向速到B点，再从B点出发向南偏西15°方向速到C点，则∠ABC等于……………………………………………………………（ ）
（A）75° （B）105° （C）45° （D）135°
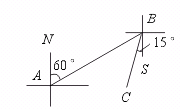
【提示】按要求画出图形再计算
∵ NA∥BS，
∴ ∠NAB＝∠SBA＝60°．
∵ ∠SBC＝15°，
∴ ∠ABC＝∠SBA－∠SBC＝60°－15°＝45°．
【答案】C．
（四）解答题（本题5分）
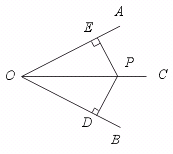
22．根据命题“角平分线上的点到角的两边距离相等”，画出图形，并结合图形写出已知、求证（不证明）.
【答案】
已知：OC平分∠AOB，P是OC上任意一点．PD⊥OB，PE⊥OA，垂足分别是D、E．
求证：PE＝PD．
五、计算题（第23、24题，每题5分．第25、26题每题6分，共22分）
23．如图，AB∥CD∥PN，∠ABC＝50°，∠CPN＝150°．求∠BCP的度数．
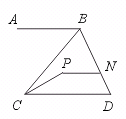
【提示】由AB∥CD，∠ABC＝50°可得∠BCD＝50°．
由PN∥CD，∠CPN＝150°，可得∠PCD＝30°．
∴ ∠BCP＝∠BCD－∠PCD＝50°－30°＝20°．
【答案】20°．
24．如图，∠CAB＝100°，∠ABF＝110°，AC∥PD，BF∥PE，求∠DPE的度数．
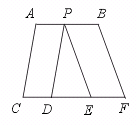
【提示】由AC∥PD，∠CAB＝100°，可得∠APD＝80°．
同理可求∠BPE＝70°．
∴ ∠DPE＝180°－∠APD－∠BPE＝180°－80°－70°＝30°．
【答案】30°．
25．如图，DB∥FG∥EC，∠ABD＝60°，∠ACE＝36°，AP平分∠BAC．
求∠PAG的度数．
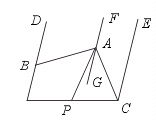
【提示】由DB∥FG∥EC，可得
∠BAC＝∠BAG＋∠CAG
＝∠DBA＋∠ACE
＝60°＋36°＝96°．
由AP平分∠BAC得∠CAP＝∠BAC＝×96°＝48°．
由FG∥EC得∠GAC＝ACE＝36°．
∴ ∠PAG＝48°－36°＝12°．
【答案】12°．
26．如图，AB∥CD，∠1＝115°，∠2＝140°，求∠3的度数．
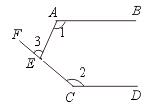
【提示】过点E作EG∥AB．
∵ AB∥CD由平行公理推论可得EG∥CD．
由此可求得∠AEC的度数．由平角定义可求得∠3的度数．
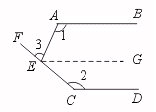
【答案】75°．
（五）证明题（每题6分，共24分）
27．已知：如图．AB∥CD，∠B＝∠C．求证：∠E＝∠F．
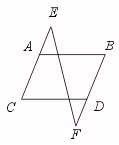
【提示】证明AC∥BD．
【答案】证明：∵ AB∥CD（已知），
∴ ∠B＝∠CDF（两直线平行，同位角相等）．
∵ ∠B＝∠C（已知），
∴ ∠CDF＝∠C（等量代换）．
∴ AC∥BD（内错角相等，两直线平行）．
∴ ∠E＝∠F（两直线平行，内错角相等）．
28．已知：如图，AC∥DE，DC∥EF，CD平分∠BCD．
求证：EF平分∠BED．
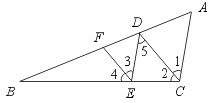
【提示】由AC∥DE．DC∥EF证∠1＝∠3．由DC∥EF证∠2＝∠4．再由CD平分∠BCA，即可证得∠3＝∠4．
【答案】证明：∵ AC∥DE（已知），
∴ ∠1＝∠5（两直线平行，内错角相等）．
同理∠5＝∠3．
∴ ∠1＝∠3（等量代换）．
∵ DC∥EF（已知），
∴ ∠2＝∠4（两直线平行，同位角相等）．
∵ CD平分∠ACB，
∴ ∠1＝∠2（角平分线定义），
∴ ∠3＝∠4（等量代换），
∴ EF平分∠BED（角平分线定义）．
29．已知：如图，AB∥CD，∠1＝∠B，∠2＝∠D．求证：BE⊥DE．
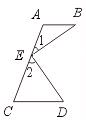
【提示】过点E作EF∥AB，证明∠BED＝90°．
【答案】证明：过点E作EF∥AB．
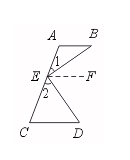∴ ∠BEF＝∠B（两直线平行，内错角相等）．
∵ ∠B＝∠1，
∴ ∠BEF＝∠1（等量代换）．
同理可证：∠DEF＝∠2．
∵ ∠1＋∠BEF＋∠DEF＋∠2＝180°（平角定义），
即2∠BEF＋2∠DEF＝180°，
∴ ∠BEF＋∠DEF＝90°（等式性质）．
即∠BED＝90°．
∴ BE⊥DE（垂直的定义）．
30．已知：如图，AB∥CD，请你观察∠E、∠B、∠D之间有什么关系，并证明你所得的结论．
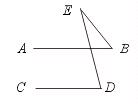
【提示】结论：∠B＋∠E＝∠D．过点E作EF∥AB．
【答案】结论：∠B＋∠E＝∠D．
证明：过点E作EF∥AB，
∴ ∠FEB＝∠B（两直线平行，内错角相等）．
∵ AB∥CD，EF∥AB，
∴ EF∥CD（平行公理推论），
∴ ∠FED＝∠D（两直线平行，内错角相等）．
∵ ∠FED＝∠FEB＋∠BED＝∠B＋∠BED，
∴ ∠B＋∠BED＝∠D（等量代换）．
本题还可添加如图所示的辅助线，请你证明∠B＋∠E＝∠D．
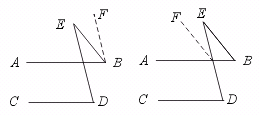
【点评】这是一道探索结论型的问题．要通过对直观图形仔细观察，大胆猜想，设定结论，再进行推理，验证结论．直观图形是观察思考的依据，准确的直观图形可引发正确的直觉思维．所以作图不可忽视．直觉思维是正确，还必须用相关的理论来验证．这样得到的结论方可靠．