中考数学第二次模拟考试试题
一、选择题（本题共32分，每小题4分）
1．
的倒数是
A、2
B、－2
C、 D、
2．一种病毒非常微小，其半径约为0.000 000 16m．将0.000 000 16用科学记数法表示为（ ）
A． 1.6×10－7 B．1.6×10－6
C． 1.6×106 D．1.6×10－8
3、点P（-2，1） 关于x轴对称的点的坐标是
A、（2，1） B、（－2，1） C、（2，-1） D、（-2，-1）
4、下列计算正确的是
A、
B、
C、
D、
5、在等边三角形、正方形、菱形、等腰梯形和圆这五个图形中，是中心对称图形的有
A．1个 B．2个 C．3个 D．4个
6、若两圆的直径是方程
的两根，圆心距为5，则这两圆的位置关系是
A、外离 B、外切 C、内切 D、相交
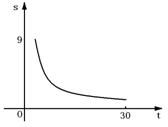
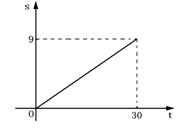
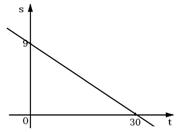
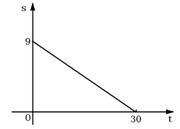
7、某地现有绿地9万公顷，由于植被遭到严重破坏，土地沙化速度竟达每年0.3万公顷. 照此速度发展下去, 设 t 年后该地剩余绿地面积为S万公顷. 在下列图象中, 能正确反映 S 与 t 的函数关系的是
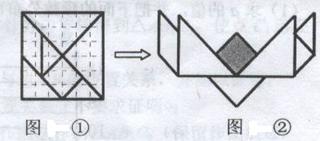
8、如图①，将一块正方形木板用虚线划分成36个全等的小正方形，然后，按其中的实线切成七块小木片，制成一副七巧板．用这副七巧板拼成图②的图案，则图②中阴影部分的面积是整个图案面积的( )．
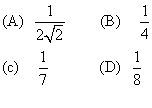
二、填空题（本题共16分，每小题4分）
9、已知△ABC∽△A′B′C′，且
，△ABC的面积为2㎝2，则△A′B′C′的面积为
㎝2.
10．
如图,点P为正方形ABCD内一点，将△ABP绕点B按顺时针方向旋转能与△CBP’重合。若BP=4, 则点P 所走过的路径长为
11、请你写出一个大于
且小于
的整数
12、如图，是一个物体的三视图，则该物体的形状是-------------------
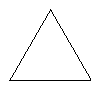
主视图 左视图
俯视图
三、解答题（共5个小题，共25分）
13、（本小题满分5分）分解因式：
14、（本小题满分5分）解分式方程：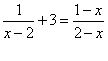
15、（本小题满分5分）
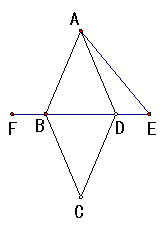如图，E、F分别是菱形ABCD对角线BD所在直线上两点，且DE＝BF.请你以F为一个端点，和图中已标明字母的某一点连成一条新的线段，猜想并证明它和图中已有的某一条线段相等（只需研究一组线段相等即可）。
（1）连结________；
（2）猜想：____________；
（3）证明：
16．（本小题满分5分）
某商场家电部为了调动营业员的工作积极性，决定实行目标等级管理。商场家电部统计了每人营业员在某月的销售额，数据如下：（单位：万元）
23 17 16 20 32 30 16 15 15 26
15 32 23 17 15 15 28 28 16 21
（1）这组数据的众数为_________________万元；中位数为_________________万元。（2分）
（2）商场规定月销售额达到或超过25万元为A级，低于19万元为C级，其他为B级，为了使商场负责人对各等级人数比例情况一目了然，请作出扇形统计图。（4分）
17、（本小题满分5分）
四、解答题（本题满分5分）
18、某校有A、B两个餐厅，甲、乙二名学生各自随机选择其中的一个餐厅用餐。
（1）求甲、乙二名学生在同一个餐厅用餐的概率。
（2）求甲、乙二名学生中至少有一人在B餐厅用餐的概率。
五、解答题（共2个小题，共10分）
19、（本小题满分5分）
20、（本小题满分5分）
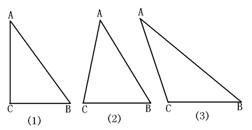
如图，△ABC中，BC=a，AC=b，AB=c.若∠C=90度，如图（1）,根据勾股定理，则
，若△ABC不是直角三角形，如图（2）和图（3），请你类比勾股定理，试猜想
与
的关系，并证明你的结论。
六、解答题（共2个小题，共10分）
21、（本小题满分5分）
22、（本小题满分5分）
已知反比例函数
和一次函数
。
⑴ 若一次函数和反比例函数的图象交于点（－3，m）求m和k的值．
⑵ 当k满足什么条件时．这两个函数的图象有两个不同的交点？
⑶ 当k=－2时，设（2）中的两个函数图象的交点分别为 A、B，试判断A、B两点分别在第几象限，∠AOB是锐角还是钝角（只要求直接写出结论）．
七、解答题（本小题满分6分）
23．在正常情况下，一个人在运动时所能承受的每分钟心跳的最高次数S（次/分）是这个人年龄n（岁）的一次函数。
（1）根据以上信息，求在正常情况下，S关于n的函数关系式；
（2）若一位63岁的人在跑步，医生在途中给他测得10秒心跳为26次，问：他是否有危险？为什么？
八、（本题满分8分）
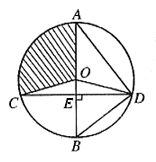
24、如图,已知
的直径AB垂直于弦CD于E,连结AD、BD、OC、OD，且OD=5。
（1） 若
，求CD的长；
（2） 若
，求扇形OAC（阴影部分）的面积（结果保留
）
九、解答题（本小题满分８分）
25．如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(4,0),(4,3).动点M、N分别从O、B同时出发，以每秒1个单位的速度运动。其中，点M沿OA向终点A运动，点N沿BC向终点C运动。过点M作MP⊥OA，交AC于P，连结NP。已知动点运动了x秒。
（1）P点的坐标为（ ， ）（用含x的代数式表示）；
（2）试求△NPC面积S的表达式，并求出面积S的最大值及相应的x值；
（3）当x为何值时，△NPC是一个等腰三角形？简要说明理由。
