★智闯三关 发挥聪明睿智,关公怎比我强
核心知识----基础关
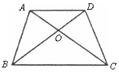
1.如图,在等腰梯形![]() 中,
中,![]() ,对角线
,对角线![]() 相交于点
相交于点![]() ,有如下四个 结论:①
,有如下四个 结论:①![]() ;②
;②![]() ;③等腰梯形
;③等腰梯形![]() 是中心对称图形;④
是中心对称图形;④![]() .则正确的结论是( )
.则正确的结论是( )
 A.①④
A.①④
B.②③
C.①②③
|
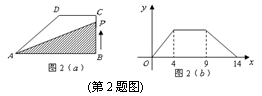
2.如图2(![]() ),在直角梯形
),在直角梯形![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从
从![]() 点出发,由
点出发,由![]() 沿边运动,设点
沿边运动,设点![]() 运动的路程为
运动的路程为![]() ,
,![]() 的面积为
的面积为![]() ,如果关于
,如果关于![]() 的函数
的函数![]() 的图象如图2(
的图象如图2(![]() ),则
),则![]() 的面积为( B )
的面积为( B )
A.10 B.16 C.18 D.32
 |
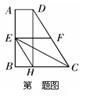
3.如图:在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为梯形的中位线,
为梯形的中位线,![]() 为梯形的高,则下列结论:①
为梯形的高,则下列结论:①![]() ,②四边形
,②四边形![]() 为菱形,③
为菱形,③![]() ,④以
,④以![]() 为直径的圆与
为直径的圆与![]() 相切于点
相切于点![]() ,其中正确结论的个数为( B ).
,其中正确结论的个数为( B ).
 A.4 B.3
A.4 B.3
|
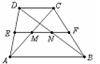
4.如图,在梯形ABCD中,AB//CD,中位线EF与对角线AC、BD交于M、N两点,若EF=18cm,MN=8cm,则AB的长等于( A )
 A.10cm B.13cm
A.10cm B.13cm
C.20cm D.26cm
|
5.用下列同一种图形,不能密铺的是( B )
A.三角形 B.正五边形
C.四边形 D.正六边形
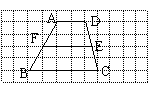 6.如图,梯形ABCD在边长为1的小正方形网格中位置如图所示,EF为中位线,则S梯形ADEF:S梯形EFBC=( )
6.如图,梯形ABCD在边长为1的小正方形网格中位置如图所示,EF为中位线,则S梯形ADEF:S梯形EFBC=( )
A 2:5
B.11:17
C C.1:2
|
核心能力-----技能关
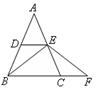 7.如图5,在
7.如图5,在![]() 中,
中,![]() ,点
,点![]() 分别是
分别是![]() 的中点,
的中点,![]() 是
是![]() 延长线上的一点,且
延长线上的一点,且![]() .
.
(1)求证:![]() ;
;
|
证明:(1)![]() 分别为
分别为![]() 的中点,
的中点,
![]() 为中位线.
为中位线.![]() ,且
,且![]() ;
;
又![]() ,
,![]() .
.
(2)连结![]() .由(1)可得
.由(1)可得![]() ,且
,且![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]() .
.
![]() ,且
,且![]() 为中位线,
为中位线,![]() 四边形
四边形![]() 为等腰梯形,
为等腰梯形,
又![]() 为等腰梯形
为等腰梯形![]() 的对角线,
的对角线,![]() ,
,![]() .
.
8.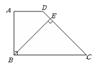 (2006 北京)已知:如图,在梯形
(2006 北京)已知:如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() .
.
求:![]() 的长.
的长.
|
解:如图,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
∵![]() ,
,
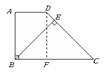 ∴四边形
∴四边形![]() 是平行四边形.
是平行四边形.
∴![]() .
.
由![]() ,
,
得![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
由![]() , 求得
, 求得![]() .
.
∴![]() .
.
在![]() 中,
中,![]() ,
,
![]() .求得
.求得![]() .
.
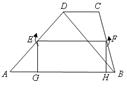 9.如图,梯形
9.如图,梯形![]() 中,
中,![]() ,
,![]() 是中位线,
是中位线,![]() 于
于![]() ,
,![]() 于
于![]() ,梯形的高
,梯形的高![]() .沿着
.沿着![]() 分别把
分别把![]() ,
,![]() 剪开,然后按图中箭头所指方向,分别绕着点
剪开,然后按图中箭头所指方向,分别绕着点![]() 旋转
旋转![]() ,将会得到一个什么样的四边形?简述理由.
,将会得到一个什么样的四边形?简述理由.
|
解:将会得到一个正方形,理由如下:
![]() ,
,
![]() .
.
![]() 是梯形
是梯形![]() 的中位线,
的中位线,
![]() ,
,
![]() .
.
![]() 梯形的高
梯形的高![]() ,
,
![]() 梯形的高
梯形的高![]() .
.
设![]() 绕点
绕点![]() 旋转
旋转![]() 后点
后点![]() 落在
落在![]() 处,
处,![]() 绕点
绕点![]() 旋转
旋转![]() 后,点
后,点![]() 落在
落在![]() 处则
处则![]() ,
,![]() 在
在![]() 所在的直线上.
所在的直线上.
![]() 是梯形
是梯形![]() 的高.
的高.
![]() ,
,![]() .
.
![]() 四边形
四边形![]() 是正方形.
是正方形.
10.如图,在梯形ABCD中,AB//DC,![]() ,且AB=1,BC=2,tan∠ADC=2.
,且AB=1,BC=2,tan∠ADC=2.
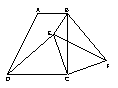 ⑴ 求证:DC=BC;
⑴ 求证:DC=BC;
|
⑶在⑵的条件下,当BE:CE=1:2,∠BEC=![]() 时,求sin∠BFE的值.
时,求sin∠BFE的值.
解:(1)过A作DC的垂线AM交DC于M,
则AM=BC=2. 又tan∠ADC=2, ∴![]() .
.
因为MC=AB=1, ∴DC=DM+MC=2即DC=BC.
(2)等腰直角三角形.
证明:∵ ![]() .
.
∴△DEC≌△BFC
∴![]() .
.
∴![]()
即△ECF是等腰直角三角形.
(3)设![]() ,则
,则![]() , ∴
, ∴![]() .
.
∵![]() ,又
,又![]() ,∴
,∴![]() .
.
∴![]() ,
,![]() .
.