概率与统计测试题
一、选择题 （每小题3分，共30分）
1．以下适合普查的是 （ C ）
A．了解一批灯泡的使用寿命 B．调查全国八年级学生的视力情况
C．评价一个班级升学考试的成绩 D．了解贵州省的家庭人均收入
2．在拼图游戏中，从图1的四张纸片中，任取两张纸片，能拼成“小房子”（如图2）的概率等于（Ｄ ）
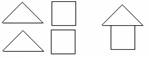A．1 B．
C．
D．
３．某电视台举行歌手大奖赛，每场比赛都有编号为1~10号共10道综合素质测试题共选手随机抽取作答。在某场比赛中，前两位选手分别抽走了2号，7号题，第3位选手抽中8号题的概率是（Ｃ ）。
A． 
B．
C．
D．
４．一鞋店试销一种新款女鞋，试销期间卖出情况如下表：
| 型号 | 22 | 22.5 | 23 | 23.5 | 24 | 24.5 | 25 |
| 数量（双） | 3 | 5 | 10 | 15 | 8 | 3 | 2 |
对于这个鞋店的经理来说最关心哪种型号鞋畅销，则下列统计量对鞋店经理来说最有意义的是（ B ）
A.．平均数 B．众数 C．中位数 D．标准差
５．某学校举行理科（含数学、物理、化学、生物四科）综合能力比赛，四科的满分都为100分．甲、乙、丙三人四科的测试成绩如下表：
| 学科 | 数学 | 物理 | 化学 | 生物 |
| 甲 | 95 | 85 | 85 | 60 |
| 乙 | 80 | 80 | 90 | 80 |
| 丙 | 70 | 90 | 80 | 95 |
综合成绩按照数学、物理、化学、生物四科测试成绩的
的比例计分，则综合成绩的第一名是（ A ）
A．甲 B．乙 C．丙 D．不确定
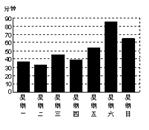
６．小红为了了解自己的学习效率，对每天在家完成课外作业所用的时间做了一周的记录，并用图表的形式表示了出来，如图所示，那么，她用时最多的一天是（ D ）
A．星期一 B．星期三 C．星期四 D．星期六
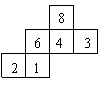
7．一个均匀的立方体各面上分别标有数字1，2，3，4，6，8，其表面展开图是如图所示，抛掷这个立方体，则朝上一面的数字恰好等于朝下一面上的数字的2倍的概率是（ A ）
A．
B．
C．
D．
| ||||
| ||||
8．某车间6月上旬生产零件的次品数如下（单位：个）：
0，2，0，2，3，0，2，3，1，2，
则在这10天中该车间生产零件的次品数的（ D ）
A.众数是4 B.中位数是1.5
C.平均数是2 D.方差是1．25
9．某快餐店用米饭加不同炒菜配制了一批盒饭，配土豆丝炒肉的有25盒，配芹菜炒肉丝的有30盒，配辣椒炒鸡蛋的有10盒，配芸豆炒肉片的有15盒．每盒盒饭的大小、外形都相同，从中任选一盒，不含辣椒的概率是（ A ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
10．某校为了了解学生课外阅读情况，随机调查了
名学生各自平均每天的课外阅读时间，并绘制成条形图（如图），据此可以估计出该校所有学生平均每人每天的课外阅读时间为（ A ）
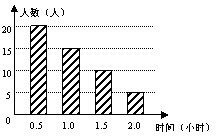Ａ．
小时 Ｂ．
小时
Ｃ．
小时 Ｄ．
小时
|
二、填空题（每小题3分，共15分）
11．“太阳每天从东方升起”，这是一个 确定 事件（填“确定”或“不确定”）．
12．某校抽查了50名九年级学生对艾滋病三种主要传播途径的知晓情况，结果如下表：
| 传播途径(种) | 0 | 1 | 2 | 3 |
| 知晓人数(人) | 3 | 7 | 15 | 25 |
估计该校九年级550名学生中，三种传播途径都知道的有 275 人。
13．一个口袋中有12个白球和若干个黑球，在不允许将球倒出来数的前提下，小亮为估计口袋中黑球的个数，采用了如下的方法：每次先从口袋中摸出10个球，求出其中白球数与10的比值，再把球放回口袋中摇匀．不断重复上述过程5次，得到的白球数与10的比值分别为：0.4，0.1，0.2，0.1，0.2．根据上述数据，小亮可估计口袋中大约有 个黑球．
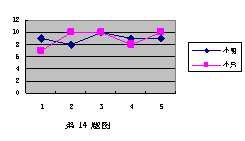
14．小明和小兵两人参加学校组织的理化实验操作测试，近期的5次测试成绩如右图所示，则小明5次成绩的方差S12与小兵5次成绩的方差S22之间的大小关系为S12 < S22．（填“＞”、“＜”、“＝”）
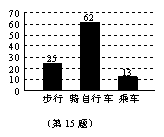15．某中学为了解学生上学方式，现随机抽取部分学生进行调查，将结果绘成条形统计图如下，由此可估计该校2400名学生中有 312 名学生是乘车上学的．
 |
三、解答题 （每小题6分，共24分）
16．根据潍坊市2006年第一季度劳动力市场职业供求状况分析，其中10个职业（职业小类）的需求人数（百人）和求职人数（百人）的数据表格如下：
| 职业 | 纺织工 | 车工 | 电子元器件制造工 | 电焊工 | 保险业务人员 | 行政办公人员 | 财会人员 | 文秘、打字员 | 卫生职业技术人员 | 计算机操作员 |
| 需求人数（百人） | 163 | 123 | 87 | 51 | 33 | 12 | 19 | 11 | 4 | 5 |
| 求职人数（百人） | 71 | 53 | 29 | 22 | 20 | 49 | 52 | 37 | 15 | 14 |
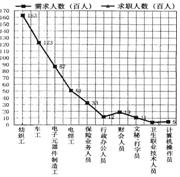（1）写出求职人数（百人）的中位数；
（2）仿照右图中需求人数折线图，画出求职人数的折线图；
（3）观察图表，比较需求人数与求职人数，你得到什么结论．（只需写出2至3项即可）
解：（1）33；
（2）见右图；
|
（只要写出合理的2条即可）
 |
17．根据北京市统计局公布的2000年，2005年北京市常住人口相关数据，绘制统计图表如下：
 |
| 年份 | 大学程度人数（指大专及以上） | 高中程度人数（含中专） | 初中程度人数 | 小学程度人数 | 其他人数 |
| 2000年 | 233 | 320 | 475 | 234 | 120 |
| 2005年 | 362 | 372 | 476 | 212 | 114 |
请利用上述统计图表提供的信息回答下列问题：
（1）从2000年到2005年北京市常住人口增加了多少万人？
（2）2005年北京市常住人口中，少儿（
岁）人口约为多少万人？
（3）请结合2000年和2005年北京市常住人口受教育程度的状况，谈谈你的看法．
解：（1）
（万人）．
故从2000年到2005年北京市常住人口增加了154万人．
（2）
（万人）．
故2005年北京市常住人口中，少儿（0～14岁）人口约为157万人．
（3）例如：依数据可得，2000年受大学教育的人口比例为16.86%，2005年受大学教育的人口比例为
．可知，受大学教育的人口比例明显增加，教育水平有所提高．
18．2007年“五一”黄金周心连心集团湖南岳阳超市，七天销售总额达120万元，具体分配情况如图．
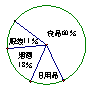（1）由图可知，日用品类销售额占总销售额的百分比为_______，日用品类销售额是
______ 万元；
（2）已知2005年心连心超市在“五一”黄金周的食品类销售额是60万元，若年
增长率保持不变，请预测2007年“五一”黄周食品类销售额是多少万元？
|
（2）2006年食品类销售额为120×60%=72（万元）
设2005年到2006年的食品类的增长率为x，则60（1+x）=72，解之得x=0.2=20%，，预测2007年“五一”黄周食品类销售额为72×（1+20%）=86.4（万元）
19．不透明的口袋里装有白、黄、蓝三种颜色的乒乓球（除颜色外其余都相同），其中白球有2个，黄球有1个，现从中任意摸出一个是白球的概率为.
（1）试求袋中蓝球的个数.
（2）第一次任意摸一个球（不放回），第二次再摸一个球，请用画树状图或列表格法，求两次摸到都是白球的概率.
解：⑴设蓝球个数为
个
则由题意得
答：蓝球有1个
 |
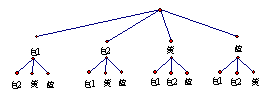∴ 两次摸到都是白球的概率 =
=
四、解答题 （每小题7分，共21分）
20．水是生命之源。为了让市民珍惜水资源，节约用水，从2006年5月1日起，武汉市居民生活用水供水价实行三级收费标准：户籍人口4人及以下的用户，每户每月用水量中，25m3(25m3)以内的部分为第一级，价格为1.90元/m3；25m3至33m3(含33m3)的部分为第二级，价格为2.45元/m3；超过33m3的部分为第三级，价格为3.00元/m3。小李家户籍人口3人，在2006年连续5个月的同一日对他家的水表止码做了如下记录：
| 时间 | 1月1日 | 2月1日 | 3月1日 | 4月1日 | 5月1日 |
| 水表止码 | 00128 | 00149 | 00169 | 00187 | 00208 |
请你利用所学统计知识解答下列问题(不考虑季节性用水量的差异)：
（1）估计2006年小李家平均每月用水量大约多少立方米？
（2）小李家从2006年5月1日起采取节水措施，若每月用水量平均平均节约2m3，且每月用水量均
在第一级，那么小李家2006年余下的8个月的水费大约共多少元？
21．2007年“五一黄金周：全国部分景点调整了门票价格，见如下数据图片：
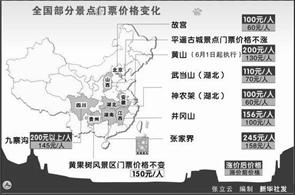
（1）按调整后门票价格从高到低的顺序，将景点名称填入表格；
| 景 点 门 票 价 格 比 较 | |||||||
| 顺序 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 景点 | 故宫 | 神农架 | |||||
| 说明 | 九寨沟门票200元以上／人、平遥古城价格不详，不作排序 | ||||||
（2）除九寨沟和平遥古城以外，对其余七个景点调整前后的门票价格绘制成条形统计图（如图）．请将上题确定的顺序代号标注在分类轴正方相应的位置；
（3）按调整的百分比计算，门票涨幅度最大的景点是：____________，其涨价的百分比为__________．
解：（1）
| 顺序 | 1 | 2 | 3 | 4 | 5 | 6 | |
| 景点 | 张家界 | 黄山 | 井冈山 | 黄果树 | 武当山 | 故宫 | 神农架 |
（2）从左到右顺序代号依次为：6、2、5、6、3、1、4
（3）涨价幅度最大的景点是：故宫和张家界，其涨价的百分比为66.7%
22某商场设计了两种促销方案：第一种是顾客在商场消费每满200元就可以从一个装有100个完全相同的球(球上分别标有数字1，2，……100)的箱子中随机摸出一个球(摸后放回)。若球上的数字是88，则返购物券500元；若球上的数字是11或77，则返购物券300元；若球上的数字能被5整除，则返购物券5元；若是其它数字，则不返购物券。第二种是顾客在商场消费每满200元直接获得购物券15元。估计促销期间将有5000人次参加活动。请你通过计算说明商家选择哪种促销方案合算些？
 |
五、解答题 （每小题10分，共30分）
23．邮政部门规定：信函重100克以内(包括100克)每20克贴邮票0.8元，不足20克重以20克计算；超过100克，先贴邮票4元，超过100克部分每100克加贴邮票2元，不足100克重以100克计算．
(1)若要寄一封重35克的信函，则需贴邮票多少元?
(2)若寄一封信函贴了6元邮票，问此信函可能有多少重?
(3)七(1)班有九位同学参加环保知识竞赛，若每份答卷重12克，每个信封重4克．请你设计方案，将这9份答卷分装在两个信封中寄出，使所贴邮票的总金额最少．
 |
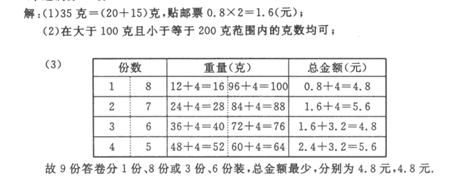2
4．今年，苏州市政府的一项实事工程就是由政府投人1 000万元资金．对城区4万户家庭的老式水龙头和13升抽水马桶进行免费改造．某社区为配合政府完成该项工作，对社区内1200户家庭中的120户进行了随机抽样调查，并汇总成下表：
| 改造 情况 | 均不 改造 | 改造水龙头 | 改造马桶 | ||||
| 1个 | 2个 | 3个 | 4个 | 1个 | 2个 | ||
| 户数 | 20 | 31 | 28 | 21 | 12 | 69 | 2 |
(1)试估计该社区需要对水龙头、马桶进行改造的家庭共有＿＿＿＿＿户；
(2)改造后．一只水龙头一年大约可节省5吨水，一只马桶一年大约可节省15吨水．试估
计该社区一年共可节约多少吨自来水?
(3)在抽样的120户家庭中．既要改造水龙头又要改造马桶的家庭共有多少户?
解：(1) 1000；
(2) 抽样的120户家庭一年共可节约用水：
（1×31+2×28+×21+4×12）× 5+(1×69+2×2)×15=198×5＋73×15=2085。
2085×
=20850(吨)。
答：该社区一年共可节约用水20850吨。
(3) 设既要改造水龙头又要改造马桶的家庭共有x户，则只改造水龙头不改造马桶的家庭共有(92-x)户，只改造马桶不改造水龙头的家庭共有(71-x)户，
∴ x+(92-x)+(71一x)=100，
∴x=63(户)。
答：既要改造水龙头又要改造马桶的家庭共有63户．
25．（一）如图，放在直角坐标系中的正方形ABCD的边长为4．现做如下实验：
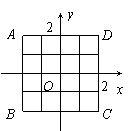抛掷一枚均匀的正四面体骰子（它有四个顶点，各顶点的点数分别是1至4这四个数字中的一个），每个顶点朝上的机会是相同的，连续抛掷两次，将骰子朝上的顶点的点数作为直角坐标系中P点的坐标(第一次的点数作横坐标，第二次的点数作纵坐标)．
（1）求P点落在正方形ABCD面上（含正方形内和边界，下同）
的概率；
（2）将正方形ABCD平移整数个单位，则是否存在一种平移，
使点P落在正方形ABCD面上的概率为
？若存在，指出其中
的一种平移方式；若不存在，请说明理由．
（二）若将（一）中所做实验用的“正四面体骰子”改为“各
面标有1 至6这六个数字中的一个的正方体骰子”，其余（实验
|
出点P落在正方形ABCD面上的概率．
【解】（一）（1） 根据题意，点P的横坐标有数字1，2，3，4四种选择，点P的纵坐标也有数字1，2，3，4四种选择，所以构成点P的坐标共有4×4 = 16种情况．其中点P的(1，1)，(1，2)，(2，1)，(2，2)四种情况将落在正方形ABCD面上，故所求的概率为
.
（2）因为要使点P落在正方形ABCD面上的概率为
，所以只能将正方
形ABCD向上或向右整数个单位平移，且使点P落在正方形面上的数目为12．存
在满足题设要求的平移方式：先将正方形ABCD上移2个单位，后右移1个单位
（先右后上亦可）；或先将正方形ABCD上移1个单位，后右移2个单位（先右后
上亦可）．
（二）点P的横、纵坐标都有数字1，2，3，4，5，6六种选择，所以构成点P的坐标
共有6×6 = 36种情况．
（1）移动0（即不移动）时，为
．
（2）先下移1个单位，后左移0.1个单位时，为
，
，即
，．
（3） 先下移1个单位，后右移1，2，3个单位时，为
，
，
，即
，
，．
（4）先左移1个单位，后下移0.1个单位时，为，，即，．
（5） 先左移1个单位，后上移1，2，3个单位时，为，，，即，，．
（6）上移1，2，3个单位时，为
，
，
，即
，
，
．
（7）右移1，2，3个单位时，为，，，即，，．
（8）先上移1个单位，后右移1，2，3个单位时，为
，
，
，即
，
，
．
（9）先上移2个单位，后右移1，2，3个单位时，为，
，
，即，
，
．
（10）先上移3个单位，后右移1，2，3个单位时，为，，
，即，，
．
（11）正方形下移或左移超过1个单位时，点P落在正方形ABCD面上的概率为0．在此点P落在正方形ABCD面上的概率（不同）为：
0，，，，，，，，，，，，，，．