中考试题分类汇编—概率
1．下列说法正确的是 （ ）D
A．一颗质地均匀的骰子已连续抛掷了2000次，其中，抛掷出5点的次数最少，则第2001
次一定抛掷出5点
B.某种彩票中奖的概率是1%，因此买100张该种彩票一定会中奖
C．天气预报说明天下雨的概率是50％．所以明天将有一半时间在下雨
D.抛掷一枚图钉，钉尖触地和钉尖朝上的概率不相等
2.同时抛掷两枚硬币，每次出现正面都向上的概率为（ ）A
3.下列事件是心然事件的是（ C ）
A、明天要下雨
B、打开电视机，正在直播足球比赛
C、抛掷一枚正方体骰子，掷得的点数不会小于1
D、买一张3D彩票，一定会中一等奖
4. 袋中有4个除颜色外其余都相同的小球，其中1个红色，1个黑色，2个白色. 现随机从袋中摸取一球，则摸出的球为白色的概率为（ ）B
A．1 B. 
C．
D. 
5. 在掷一枚硬币的试验中，着地时反面向上的概率为. 如果掷一枚硬币150次，则着地时正面向上约 次. 75
6、要在一只不透明的袋中放入若干个只有颜色不同的乒乓球，搅匀后，使得从袋中任意摸出一个乒乓球是黄色的概率是2/5，可以怎样放球
（只写一种）两个黄球，三个白球
7．某电视台综艺节目从接到的5000个热线电话中，抽取10名“幸运观众”，小颖打通了一次热线电话，她成为“幸运观众”的概率是
．
或0.002
8.在抛掷一枚普通正六面体骰子的过程中，出现点数为2的概率是 .
9.一副去掉大小王的扑克牌（共52张），洗匀后，摸到红桃的机会 摸到J、Q、K的机会（填“＜，＞或＝” ）. ＞
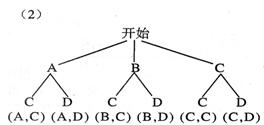
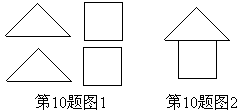10．在拼图游戏中，从图1的四张纸片中，任取两张纸片，能拼成“小房子”（如图2）的概率等于（ D ）有
A.1 B.
C.
D.
11．在围棋盒中有x颗黑色棋子和y颗白色棋子，从盒中随机地取出一个棋子，如果它是黑色棋子的概率是
.
（1）试写出y与x的函数关系式.wyyyywy=yyw.1230.org 初中数学资源网
（2）若往盒中再放进10颗黑色棋子，则取得黑色棋子的概率变为
，求x和y的值.
（1）由已知得，
= 
，故y=
x;（2）由（1）得3y=5x,又
=，故2x+20=x+y+10,即y=x+10,从而3（x+10）=5x,x=15,y=25.
12．如图，一条毛毛虫要从A处去吃树叶，毛毛虫在交叉路口B、C、D、E处选择任何树杈都是可能的，求下列概率：
（1）吃到树叶1的概率；
（2）吃到树叶的概率；
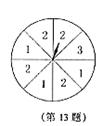
13．从标有1，3，4，6，8的五张卡片中随机抽取两张，和为奇数的概率是
14. 把一副普通扑克牌中的4张；黑桃2，红心3，梅花4，黑桃5，洗匀后正面朝下放在桌面上.
（1）从中随机抽取一张牌是黑桃的概率是多少？
（2）从中随机抽取一张，再从剩下的牌中随机抽取另一张. 请用表格或树状图表示抽取的两张牌牌面数字所有可能出现的结果，并求抽取的两张牌牌面数字之和大于7的概率.
解：（1）从中随机抽取一张牌是黑桃的概率为 
（2）抽取的两张牌牌面数字所有可能出现的结果用表格表示如下：
|
| 2 | 3 | 4 | 5 |
| 2 |
| （2，3） | （2，4） | （2，5） |
| 3 | （3，2） | （3，4） | （3，5） | |
| 4 | （4，2） | （4，3） | （4，5） | |
| 5 | （5，2） | （5，3） | （5，4） |
也可树状图表示如下：
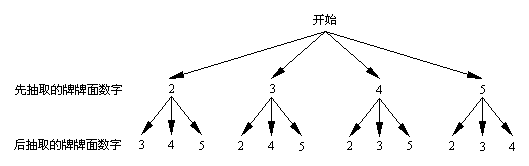
所有可能出现的结果 (2,3) (2,4) (2,5) (3,2) (3,4) (3,5) (4,2) (4,3) (4,5) (5,2) (5,3) (5,4)
由表格（或树状图）可以看出，抽取的两张牌可能出现的结果有12种，它们出现的可能性相等，而两张牌牌面数字之和大于7的结果有4种，所以抽取的两张牌牌面数字之和大于7的概率为 .
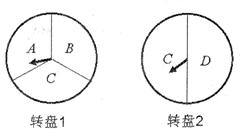15. 为举办毕业联欢会，小颖设计了一个游戏：游戏者分别转动如图的两个可以自由转动的转盘各一次，当两个转盘的指针所指字母相同时，他就可以获得一次指定一位到会者为大家表演节目的机会．
(1）利用树状图或列表的方法（只选其中一种）表示出游戏可能出现的所有结果；
(2）若小亮参加一次游戏，则他能获得这种指定机会的概率是多少？
 | |||
 | |||
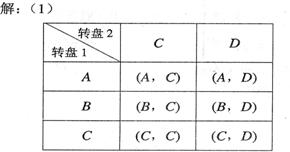∴游戏共有6种结果.
（2）参加一次游戏获得这种指定机会的概率是
.
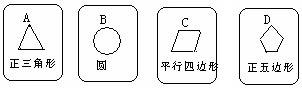16．有四张背面相同的纸牌A，B，C，D，其正面分别划有四个不同的稽核图形（如图）．小华将这4张纸牌背面朝上洗匀后摸出一张，放回洗匀后再摸出一张．
（1）用树状图（或列表法）表示两次模牌
所有可能出现的结果（纸牌可用A、
B、C、D表示）；
（2）求摸出两张牌面图形都是中心对称
图形的纸牌的概率．
 |
第一次摸的牌
第二次摸的牌
（列表略）
（2）
17.甲、乙两队进行拔河比赛，裁判员让两队队长用“石头、剪子、布”的手势方式选择场地位置.规则是：石头胜剪子，剪子胜布，布胜石头，手势相同再决胜负.请你说明裁判员的这种作法对甲、乙双方是否公平，为什么？(用树状图或列表法解答)
解：裁判员的这种作法对甲、乙双方是公平的.
理由：方法一：用列表法得出所有可能的结果如下：
| 甲 | 乙 | ||
| 石头 | 剪子 | 布 | |
| 石头 | (石头，石头) | (石头，剪子) | (石头，布) |
| 剪子 | (剪子，石头) 21. | (剪子，剪子) | (剪子，布) |
| 布 | (布，石头) | (布，剪子) | (布，布) |
根据表格得，P(甲获胜)=
，P(乙获胜）=
∵P(甲获胜)=P(乙获胜)，
∴裁判员这种作法对甲、乙双方是公平的.
方法二：用树状图得出所有可能的结果如下：
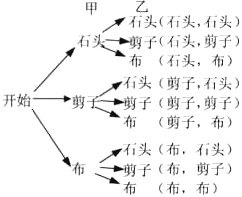
根据树状图，P(甲获胜)=，P(乙获胜）=.
∵P(甲获胜)=P(乙获胜)，
∴裁判员这种作法对甲、乙双方是公平的.
18. 甲、乙、丙、丁四人参加某校招聘教师考试，试后甲、乙两人去询问成绩。请你根据下面回答者对甲、乙两人回答的内容进行分析，则这四人的名次排列共可能有 种不同情况.4
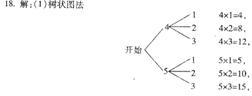
19．甲、乙两人用如图所示的两个分格均匀的转盘做游戏：分别转动两个转盘，若转盘停止后，指针指向一个数字（若指针恰好停在分格线上，则重转一次），用所指的两个数字作乘积，如果积大于10，那么甲获胜；如果积不大于10，那么乙获胜。清你解决下列问题：
(l）利用树状图（或列表）的方法表示游戏所有可能出现的结果；
(2）求甲、乙两人获胜的概率。
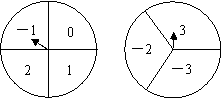20．（1）如图所示的转盘中指针落在每个数字上的机会相等，现同时转动A、B两转盘，停止后，指针各指向一个数字.小彬和小颖利用这个转盘做游戏：若两数之积为非负数则小彬胜，否则，小颖胜.你认为这个游戏对双方公平吗？ .（直接写出结果）
不公平，因为共有12个积，而其中的非负数有7个，
故P（小彬胜）=
，P（小颖胜）=
，
P（小彬胜）＞P（小颖胜），所以不公平.
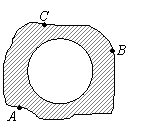（2）小明在操场上做游戏，他发现地上有一个不规则的封闭图形ABC.为了知道它的面积，小明在封闭图形内划出了一个半径为1米的圆，在不远处向圈内掷石子，且记录如下：
|
| 50次 | 150次 | 300次 |
| 石子落在⊙O内(含⊙O上)的次数m | 14 | 43 | 93 |
| 石子落在阴影内的次数n | 19 | 85 | 186 |
你能否求出封闭图形ABC的面积？试试看.
由表可知，P（石子落在⊙O内）=
=0.5，故可估计S⊙O： S封闭图形ABC=0.5，因为S⊙O=
，
所以S封闭图形ABC=2（m2）.
21．妞妞和她的爸爸玩“锤子、剪刀、布”游戏．每次用一只手可以出锤子、剪刀、布三种手势之一，规则是锤子赢剪刀、剪刀赢布、布赢锤子，若两人出相同手势，则算打平．
(1)你帮妞妞算算爸爸出“锤子”手势的概率是多少?
答：
(2)妞妞决定这次出“布”手势，妞妞赢的概率有多大?
答：
(3)妞妞和爸爸出相同手势的概率是多少?
答：
22．某商场在“五一”期间推出购物摸奖活动，摸奖箱内有除颜色以外完全相同的红色、白色乒乓球各两个．顾客摸奖时，一次摸出两个球，如果两个球的颜色相同就得奖，颜色不同则不得奖．那么顾客摸奖一次，得奖的概率是 ．
23.晓明玩转盘游戏，当他转动如图所示的转盘，转盘停止时指针指向2的概率是_________.（或0.5，50%）
24.袋中共有5个大小相同的红球、白球，任意摸出一球为红球的概率是
.
（1）袋中红球、白球各有几个？
（2）任意摸出两个球均为红球的概率是_________________.
（1）
答：袋中有2个红球，3个白球. （2）
25. 王强与李刚两位同学在学习“概率”时．做抛骰子(均匀正方体形状)实验，他们共抛了54次，出现向上点数的次数如下表：
| 向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现次数 | 6 | 9 | 5 | 8 | 16 | 10 |
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率．
(2)王强说：“根据实验，一次试验中出现向上点数为5的概率最大．”
李刚说：“如果抛540次，那么出现向上点数为6的次数正好是100次．”
请判断王强和李刚说法的对错．
(3)如果王强与李刚各抛一枚骰子．求出现向上点数之和为3的倍数的概率．
(1)出现向上点数为3的频率为
，出现向上点数为5的频率为
(2)都错
(3)画树状图或列表或简单说理(正确)，概率P=
.
26．在一个不透明的箱子里放有除颜色外，其余都相同的4个小球，其中红球3个、白球1个．搅匀后，从中同时摸出2个小球，请你写出这个实验中的一个可能事件： . 例如：“摸出2个红球”；
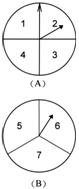27．甲乙两人在玩转盘游戏时，把转盘A、B分别分成4等份、3等份，并在每一份内标上数字，如图所示. 游戏规定，转动两个转盘停止后，指针所指的两个数字之和为奇数时，甲获胜；为偶数时，乙获胜．
（1）用列表法（或画树状图）求甲获胜的概率；
（2）你认为这个游戏规则对双方公平吗？请简要说明理由.
解：⑴（法1）画树状图
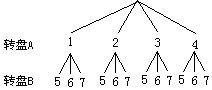
由上图可知，所有等可能的结果共有12种，指针所指的两个数字之和为奇数的结
果有6种. ∴P（和为奇数）=0.5
（法2）列表如下：
|
| 1 | 2 | 3 | 4 | ||||||||||||||
| 5 | 1+5=6 | 2+5=7 | 3+5=8 | 4+5=9 | ||||||||||||||
| 6 | 1+6=7 | 2+6=8 | 3+6=9 | 4+6=10 | ||||||||||||||
| 7 | 1+7=8 | 2+7=9 | 3+7=10 | 4+7=11 |
由上表可知，所有等可能的结果共有12种，指针所指的两个数字之和为奇数的结
果有6种. ∴P（和为奇数）=0.5
⑵∵P（和为奇数）=0.5
∴P（和为偶数）=0.5
∴这个游戏规则对双方是公平的.
28．有2名男生和2名女生，王老师要随机地、两两一对地为他们排座位，一男一女排在一起的概率是( ) D
(A) (B) (C) (D)
29．已知函数y＝x－5，令x＝
、1、
、2、
、3、
、4、
、5，可得函数图象上的十个点．在这十个点中随机取两个点P（x1，y1）、Q（x2，y2），则P、Q两点在同一反比例函数图象上的概率是（ B ）
（A）
（B）
（C）
（D）
30．五一前某电器商场在晋江开业，若他们发的1000张奖券中有200张可
以中奖，则从中任抽1张能中奖的概率为 . 
31．下列事件中，是确定事件的是（ C ）
A．明年五一晋江会下雨 B．中国人都穿晋江生产的鞋
C．地球总是绕着太阳转 D．去北京要乘火车
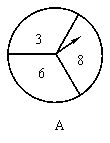
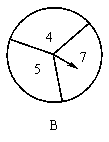
32．如图，是由转盘和箭头组成的两个装置，装置A、B的转盘分别被平均分成三部分，装置A上的数字是3、6、8；装置B上的数字是4、5、7；这两个装置除了表面数字不同外，其他构造均相同，小东和小明分别同时转动A、B两个转盘（一人转一个），如果我们规定箭头停留在较大数字的一方获胜（如：若A、B两个转盘的箭头分别停在6、4上，则小东获胜，若箭头恰好停在分界线上，则重新转一次），请用树状图或列表加以分析说明这个游戏公平吗？
 |  | ||
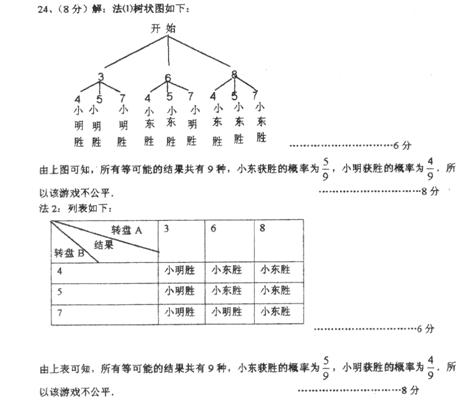
33．如图13，有两个可以自由转动的均匀转盘
．转盘
被平均分成
等份，分别标上
三个数字；转盘
被平均分成4等份，分别标上
四个数字．有人为甲、乙两人设计了一个游戏规则；自由转动转盘与，转盘停止后，指针各指向一个数字，将指针所指的两个数字相加，如果和是6，那么甲获胜，否则为乙获胜．
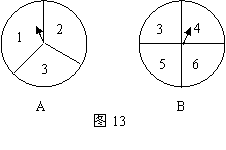你认为这样的游戏规则是否公平？如果公平，请说明理由；如果不公平，怎样修改规则才能使游戏对双方公平？
解：不公平．
（和为6）
，
甲、乙获胜的概率不相等
不公平．
规则改为：和是6或7，甲胜；否则乙胜．
（和为奇数，甲胜；和为偶数，乙胜；或和小于7，甲胜；和大于等于7，乙胜．答案不唯一．） 列 表
|
| 3 | 4 | 5 | 6 |
| 1 | 4 | 5 | 6 | 7 |
| 2 | 5 | 6 | 7 | 8 |
| 3 | 6 | 7 | 8 | 9 |
B34．抛掷一个质地均匀的正方体骰子，骰子的六个面上分别刻有
1至6的点数，则掷得点数是2的概率是
. 
35．下列事件中，是必然事件的为（ ）A
A．我市夏季的平均气温比冬季的平均气温高；
B．每周的星期日一定是晴天；
C．打开电视机，正在播放动画片；
D．掷一枚均匀硬币，正面一定朝上.
36．在两个布袋中分别装有三个小球，这三个小球的颜色分别为红色、白色、绿色，其他没有区别.把两袋小球都搅匀后，再分别从两袋中各取出一个小球，试求取出两个相同颜色小球的概率（要求用树状图个或列表方法求解）.
解：（解法一）
列举所有等可能结果，画树状图：
布袋1
红
白
绿
布袋2 红白绿 红白绿 红白绿
由上图2可知，所有等可能结果共有9种，两个相同颜色小球的结果共3种，
∴P（相同颜色）=
（解法二）列表如下：
|
 | 红 | 白 | 绿 | ||||||
| 红 | （红，红） | （红，白） | （红，绿） | ||||||
| 白 | （白，红） | （白，白） | （白，绿） | ||||||
| 绿 | （绿，红） | （绿，白） | （绿，绿） |
由上表可知，所有等可能结果共有9种，两个相同颜色小球的结果共3种，
∴P（相同颜色）=
37．小明与小亮玩掷骰子游戏，有两个均匀的正方体骰子，六个面上分别写有1，2，3，4，5，6这六个数．如果掷出的两个骰子的两个数的和为奇数则小明赢，如果掷出的两个骰子的两个数的和为偶数则小亮赢，则小明赢的概率是 ．
38．投一枚均匀的正方体骰子，面朝上的点数是5的概率是 ．
39. 某初级中学准备组织学生参加A、B、C三类课外活动，规定每班2人参加A类课外活动、3人参加B类课外活动、5人参加C类课外活动，每人只能参加一项课外活动，各班采取抽签的方式产生上报名单. 假设该校每班学生人数均为40人，请给出下列问题的答案(给出结果即可)：
(1) 该校某个学生恰能参加C类课外活动的概率是多少？
(2) 该校某个学生恰能参加其中一类课外活动的概率是多少？
(3) 若以小球作为替代物进行以上抽签模拟实验，一个同学提供了部分实验操作：① 准备40个小球；②把小球按2∶3∶5的比例涂成三种颜色；③ 让用于实验的小球有且只有2个为A类标记、有且只有3个为B类标记、有且只有5个为C类标记；④ 为增大摸中某类小球的机会，将小球放入透明的玻璃缸中以便观察 . 你认为其中哪些操作是正确的(指出所有正确操作的序号)？
18.(1) . (2) .(3) ①，③.
40. 同时抛掷两枚质地均匀的正方体骰子(骰子每一面的点数分别是从1到6这六个数字中的一个)，以下说法正确的是（ ）C
A．掷出两个1点是不可能事件 B．掷出两个骰子的点数和为6是必然事件
C．掷出两个6点是随机事件 D．掷出两个骰子的点数和为14是随机事件
41．用长为5cm，6cm，7cm的三条线段围成三角形的事件是（ ）B
A．随机事件 B．必然事件 C．不可能事件 D．以上都不是
42．（2006·南宁市）在元旦游园晚会上有一个闯关活动：将5张分别画有等腰梯形、圆、平行四边形、等腰三角形、菱形的卡片任意摆放，将有图形的一面朝下，从中任意翻开一张，如果翻开的图形是轴对称图形，就可以过关．那么一次过关的概率是（ ）D
Ａ．
Ｂ． Ｃ．
Ｄ．
43. 抛掷红、蓝两枚六面编号分别为1~6（整数）的质地均匀的正方体骰子，将红色和蓝色骰子正面朝上的编号分别作为二次函数y=x2+mx+n的一次项系数m 和常数项n的值。
（1）问这样可以得到多少个不同形式的二次函数？（只需写出结果）
（2）请求出抛掷红、蓝骰子各一次，得到的二次函数图象顶点恰好在x轴上的概率是多少？并说明理由。
 |
44．“石头、剪刀、布” 是民间广为流传的游戏，游戏时，双方每次只能做“石头”、“剪刀”、“布”这三种手势中的一种．假定双方每次都是等可能的做这三种手势．
问：小强和小刚在一次游戏时
（1）两个人同时出现“石头”手势的概率是多少？
（2）两个人出现不同手势的概率是多少？
解：可列表格如下：
|
| 石头 | 剪刀 | 布 |
| 石头 | （石，石） | （石，剪） | （石，布） |
| 剪刀 | （剪，石） | （剪，剪） | （剪，布） |
| 布 | （布，石） | （布，剪） | （布，布） |
（1）
（石，石）
（2）（不同手势）
45．有2名男生和2名女生，王老师要随机地、两两一对地为他们排座位，一男一女排在一起的概率是( ) D
(A) (B) (C) (D)
46．有四张背面相同的纸牌A，B，C，D，其正面分别划有四个不同的稽核图形（如图）．小华将这4张纸牌背面朝上洗匀后摸出一张，放回洗匀后再摸出一张．
（1）用树状图（或列表法）表示两次模牌
所有可能出现的结果（纸牌可用A、
B、C、D表示）；
（2）求摸出两张牌面图形都是中心对称
图形的纸牌的概率．
|
第一次摸的牌
第二次摸的牌
（列表略）
（2）
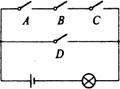47如图．电路图上有四个开关A、B、C、D和一个小灯泡，闭合开关D或同时闭合开关A，B，C都可使小灯泡发光。
(1)任意闭合其中一个开关，则小灯泡发光的概率等于＿＿＿；
(2)任意闭合其中两个开关，请用画树状图或列表的方法求出小
灯泡发光的概率．
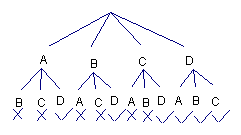解：(1)
．
(2)正确画出树状图(或列表)
第1个开关
第2个开关
结果
任意闭合其中两个开关的情况共有12种，其中能使小灯泡发光的情况有6种
小灯泡发光的概率是
48. 现有A、B两枚均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6）.用小莉掷A立方体朝上的数字为
、小明掷B立方体朝上的数字为
来确定点P（
），那么它们各掷一次所确定的点P落在已知抛物线
上的概率为（ ）B
A. 
B.
C.
D.
48．一对酷爱运动的夫妇，让他们刚满周岁的孩子拼排3块分别写有“20”、“08”、“北京”的字块．假如小孩将字块横着正排，则该小孩能够排成“2008北京”或“北京2008”的概率是（ ）C
Ａ． Ｂ． Ｃ． Ｄ．
49．“太阳从西边出来”所描述的是一个___________事件．不可能
50．一个袋中装有6个红球、4个黑球、2个白球，每个球除颜色外完全相同，从袋中任意摸出一个球，那么摸出 球的可能性最大．红
51．小明与小华在玩一个掷飞镖游戏，如图
甲是一个把两个同心圆平均分成8份的靶，当飞镖掷中阴影部分时，小明胜，否则小华胜（没有掷中靶或掷到边界线时重掷）．
（1）不考虑其他因素，你认为这个游戏公平吗？说明理由．
（2）请你在图乙中，设计一个不同于图甲的方案，使游戏双方公平．
 |
解：（1）这个游戏公平．
根据图
甲的对称性，阴影部分的面积等于圆面积的一半，
这个游戏公平．
（2）把图乙中的同心圆平均分成偶数等分，再把其中的一半作为阴影部分即可．（图略）
52．下列事件是必然事件的是（ ）C
A．今年10月1日湛江的天气一定是晴天
B．2008年奥运会刘翔一定能夺得110米跨栏冠军
C．当室外温度低于
℃时，将一碗清水放在室外会结冰
D．打开电视，正在播广告
53．在一个不透明的口袋中，有大小、形状完全相同，颜色不同的球15个，从中摸出红球的概率为，则袋中红球的个数为（ ）C
A．10 B．15 C．5 D．3
54．某市电视台在今年5月举办的“开心就唱”歌手大赛活动中，号召观众发短信为参赛者投支持票，投票短信每1万条为1组，每组抽出1个一等奖，3个二等奖，6个三等奖．张艺同学发了1条短信，她的获奖概率是（ ）B
A．
B．
C．
D．
55．如图，是从一副扑克牌中取出的两组牌，分别是红桃1，2，3和方块1，2，3，将它们的背面朝上分别重新洗牌后，再从两组牌中各摸出一张．
|
（2）求摸出的两张牌的牌面数字之和不小于5的概率．
（1）所有可能出现的结果可用下表表示：
|
| 1 | 2 | 3 |
| 1 |
|
|
|
| 2 |
|
|
|
| 3 |
|
|
|
（2）由上表可知牌面的数字之和不小于5的概率为：
．
56．如图2，是一个圆形转盘，现按
分成四个部分，分别涂上红，黄，蓝，绿四种颜色，自由转动转盘，停止后指针落在绿色区域的概率为
．
57．甲、乙两超市同时开业，为了吸引顾客，都举行有奖酬宾活动：凡购物满100元，均可得到一次摸奖的机会，在一个纸盒里装有2个红球和2个白球，除颜色外，其它全部相同，摸奖者一次从中摸出两个球，根据球的颜色决定送礼金券的多少（如下表）．
甲超市
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券（元） | 5 | 10 | 5 |
乙超市
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券（元） | 10 | 5 | 10 |
如果只考虑中奖因素，你将会选择去哪个超市购物？请说明理由．
解：去甲超市购物一次摸奖获10元礼金券的概率是P(甲)
去乙超市购物一次摸奖获10元礼金券的概率是P(乙)
所以我选择去甲超市购物．
58．小明将一把钥匙放进自己家中的抽屉中，他记不清到底放进三个抽屉中的哪一个了，那么他一次选对抽屉的概率是 ．
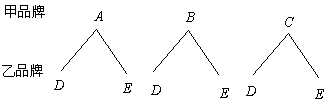
59．某公司现有甲、乙两种品牌的计算器，甲品牌计算器有
三种不同的型号，乙品牌计算器有
两种不同的型号，新华中学要从甲、乙两种品牌的计算器中各选购一种型号的计算器．
（1）写出所有的选购方案（利用树状图或列表方法表示）；
（2）如果（1）中各种选购方案被选中的可能性相同，那么
型号计算器被选中的概率是多少？
（3）现知新华中学购买甲、乙两种品牌计算器共40个（价格如图所示），恰好用了1000元人民币，其中甲品牌计算器为型号计算器，求购买的型号计算器有多少个？
解：（1）树状图表示如下：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
甲
列表表示如下：
有6种可能结果：
．
（2）因为选中型号计算器有2种方案，即
，所以型号计算器被选中的概率是
．
（3）由（2）可知，当选用方案
时，设购买型号，
型号计算器分别为
个，
根据题意，得
解得
经检验不符合题意，舍去；
当选用方案
时，设购买型号、
型号计算器分别为个，
根据题意，得
解得
所以新华中学购买了5个型号计算器．
60. 有四种边长都相等的正
三角形、正方形、正五边形、正六边形瓷砖，如果任意用其中两种
瓷砖组合密铺地面，在不切割的情况下，能镶嵌成平面 图案的概率
是____.
61. 小明和哥哥得到了一张音乐演唱会的门票，两人都很想前往，可票只有一张.哥哥想了一个办法：拿8张扑克牌，将数字为3、4、7、9的四张给小明，将数字为2、5、6、8的四张留给自己，并按如下游戏方式进行确定：小明和哥哥从四张扑克牌中随机抽出一张，将抽出得到的两张扑克牌数字相加，如果和为偶数，则小明获胜，该小明去；如果和为奇数，则哥哥获胜，该哥哥去.
（1）你认为该游戏规则是否公平？请画树状图或列表予以说明；
（2）如果该游戏规则不公平，请你改变一下游戏方案，使得游戏规则公平；如果该游戏规则公平，请你制订一个不公平的游戏规则.
.解：（1）该游戏规则不公平
每次游戏可能出现的所有结果列表如下：
|
小明的 数字 | 2 | 5 | 6 | 8 |
| 3 | （2，3） | （5，3） | （6，3） | （8，3） |
| 4 | （2，4） | （5，4） | （6，4） | （8，4） |
| 7 | （2，7） | （5，7） | （6，7） | （8，7） |
| 9 | （2，9） | （5，9） | （6，9） | （8，9） |
哥哥的数字根据表格，数字之和的情况共有16种，其中和为偶数的有6种：
（5，3）、（2，4）、（6，4）、（8，4）、（5，7）、（5，9）
∴小明获胜的概率
∴哥哥获胜的概率为
∴该游戏规则不公平
（2）将小明的奇数数字扑克牌与哥哥偶数数字扑克牌对换一张
62．下列成语所描述的事件是必然事件的是（ ）D
A．水中捞月 B．拔苗助长 C．守株待兔 D．瓮中捉鳖
63．一只口袋里有相同的红、绿、蓝三种颜色的小球，其中有6个红球，
5个绿球．若任意摸出一个绿球的概率是
，则任意摸出一个蓝球的概率是 ．0.45
64．在电视台举行的“超级女生”比赛中，甲、乙、丙三位评委对选手的综合表现，分别给出“待定”或“通过” 的结论．
（1）写出三位评委给出A选手的所有可能的结论；
（2）对于选手A，只有甲、乙两位评委给出相同结论的概率是多少？
解：（1）画出树状图来说明评委给出A选手的所有可能结果：
 |
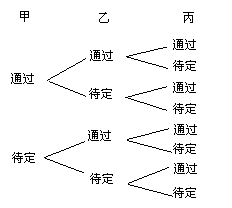（2）由上可知评委给出A选手所有可能的结果有8种．对于 A选手，“只有甲、乙两位评委给出相同结论”有2种，即“通过－通过－待定”、“待定－待定－通过”，所以对于A选手“只有甲、乙两位评委给出相同结论”的概率是
．
65． 不透明的口袋里装有白、黄、蓝三种颜色的乒乓球（除颜色外其余都相同），其中白球有2个，黄球有1个，现从中任意摸出一个是白球的概率为.
（1）试求袋中蓝球的个数.
（2）第一次任意摸一个球（不放回），第二次再摸一个球，请用画树状图或列表格法，求两次摸到都是白球的概率.
解：⑴设蓝球个数为个，则由题意得
，
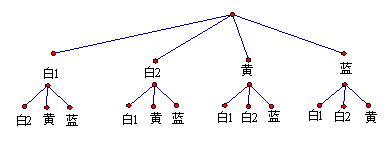答：蓝球有1个
∴ 两次摸到都是白球的概率 =
=
66.在“石头、剪子、布”的游戏中，两人做同样手势的概率是 . ；
67．在体育达标跳绳项目测试中，1分钟跳160次为达标，小敏记录了他预测时1分钟跳的次数分别为145, 155, 140, 162, 164. 则他在该次预测中达标的概率是__________． 
；
68．下列事件中，属于随机事件的是（ B ）
A.掷一枚普通正六面体骰子所得点数不超过6 B.买一张体育彩票中奖
C.太阳从西边落下
D.口袋中装有
个红球，从中摸出一个白球
69．小明和小亮玩一个游戏：三张大小、质地都相同的卡片上分别标有数字1，2，3，现将标有数字的一面朝下. 小明从中任意抽取一张，记下数字后放回洗匀，然后小亮从中任意抽取一张.，计算小明和小亮抽得的两个数字之和，如果和为奇数则小明胜，和为偶数则小亮胜．
⑴ 用列表或画树状图等方法，列出小明和小亮抽得的数字之和所有可能出现的情况；
⑵请判断该游戏对双方是否公平，并说明理由．
解：⑴（法一）列表如下：
|
| 1 | 2 | 3 | ||||||||||||
| 1 | 1+1=2 | 2+1=3 | 3+1=4 | ||||||||||||
| 2 | 1+2=3 | 2+2=4 | 3+2=5 | ||||||||||||
| 3 | 1+3=4 | 2+3=5 | 3+3=6 |
由上表可知，所有等可能的结果共有9种
（法二）画树状图略
⑵∵P（和为奇数）=
，P（和为偶数）=
∴这个游戏规则对双方是不公平的.
70．袋子里有8个白球，n个红球，经过大量实验，从中任取一个球恰好是红球的概率是则n的值是____________.16；
71． 奥地利遗传学家孟德尔发现纯种的黄豌豆和绿豌豆杂交，得到杂种第一代豌豆，它们都呈黄色。他假设纯种黄豌豆的基因是YY，纯种绿豌豆的基因是gg，则杂种第一代豌豆的基因是Yg，其中黄绿基因各一个，只要两个基因中有一个基因是Y，豌豆就呈黄色，故第一代的所有豌豆均呈黄色。第一代豌豆自交，即父的两个基因Y、g与母的两个基因Y、g再随机配对，将产生4种可能结果：
 |
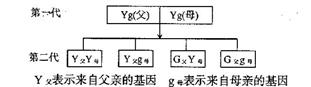(1)求第二代出现黄色豌豆的概率。
(2)如果在第二代中再选择两个品种杂交，使第三代黄色豌豆出现的概率为50%，应如何配对，请画出相应的树状图。
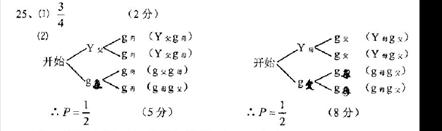
72．气象台预报“本市明天降水概率是80%”，对此信息，下面的几种说法正确的是（ D ）
Ａ．本市明天将有80%的地区降水 Ｂ．本市明天将有80%的时间降水
Ｃ．明天肯定下雨 Ｄ．明天降水的可能性比较大
73．从两副拿掉大、小王的扑克牌中，各抽取一张，两张牌都是红桃的概率是_____________．
74．一个口袋中有12个白球和若干个黑球，在不允许将球倒出来数的前提下，小亮为估计口袋中黑球的个数，采用了如下的方法：每次先从口袋中摸出10个球，求出其中白球数与10的比值，再把球放回口袋中摇匀．不断重复上述过程5次，得到的白球数与10的比值分别为：0.4，0.1，0.2，0.1，0.2．根据上述数据，小亮可估计口袋中大约有 个黑球．48
75．小明和小亮用如下的同一个转盘进行“配紫色”游戏．游戏规则如下：连续转动两次转盘，如果两次转盘转出的颜色相同或配成紫色（若其中一次转盘转出蓝色，另一次转出红色，则可配成紫色），则小明得1分，否则小亮得1分．你认为这个游戏对双方公平吗？请说明理由；若不公平，请你修改规则使游戏对双方公平．
解：
| 第二次 第一次 | 红 | 黄 | 蓝 |
| 红 | （红，红） | （红，黄） | （红，蓝） |
| 黄 | （黄，红） | （黄，黄） | （黄，蓝） |
| 蓝 | （蓝，红） | （蓝，黄） | （蓝，蓝） |
从表中可以得到：P（小明获胜）＝
，P（小亮获胜）＝．
∴小明的得分为×1＝ ， 小亮的得分为 ×1＝ ．
∵ ＞ ，∴游戏不公平．
修改规则不惟一．如若两次转出颜色相同或配成紫色，则小明得4分，否则小亮得5分
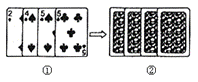76. 四张扑克牌的牌面如图①所示，将扑克牌洗均匀后，如图②背面朝上放置在桌面上。
（1）若随机抽取一张扑克牌，则牌面数字恰好为5的概率是_____________；
（2）规定游戏规则如下：若同时随机抽取两张扑克牌，抽到两张牌的牌面数字之和是偶数为胜；反之，则为负。你认为这个游戏是否公平？请说明理由.
解：（1）
（2）不公平.
画树状图如图所示：
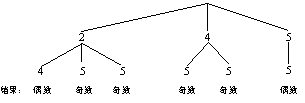
（其它方法相应给分）
所以P（和为偶数）＝
，P（和为奇数）＝
因为P（和为偶数）≠P（和为奇数），所以游戏不公平.
77. 同时抛掷两枚正方体骰子，所得点数之和为7的概率是 .
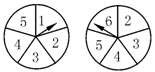78. 如图所示的两个圆盘中，指针落在每一个数上的机会均等，那么两个指针同时落在偶数上的概率是 ( ) C
A． B． C． D．
79．一个不透明的袋中装有除颜色外其余均相同的5个红球和3个黄球，从中随机摸出一个，则摸到黄球的概率是（ ）C
A、
B、
C、 
D、
80．小莉和小慧用如图所示的两个转盘做游戏，转动两个转盘各一次，若两次数字和为奇数，则小莉胜；若两次数字和为偶数，则小慧胜．这个游戏对双方公平吗？试用列表法或树状图加以分析．
解：这个游戏对双方公平．理由如下：
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
从表中可以看出，总共有
种结果，每种结果出现的可能性相同，而两数和为奇数的结果有种． 
．因此，这个游戏对双方公平．
81．其市气象局预报称：明天本市的降水概率为70%，这句话指的是 （ D ）
A. 明天本市70%的时间下雨，30%的时间不下雨
B. 明天本市70%的地区下雨，30%的地区不下雨
C. 明天本市一定下雨
D. 明天本市下雨的可能性是70%
82.下列事件是心然事件的是（ C ）
A、明天要下雨
B、打开电视机，正在直播足球比赛
C、抛掷一枚正方体骰子，掷得的点数不会小于1
D、买一张3D彩票，一定会中一等奖
83、要在一只不透明的袋中放入若干个只有颜色不同的乒乓球，搅匀后，使得从袋中任意摸出一个乒乓球是黄色的概率是 ，2/5，可以怎样放球
.（只写一种）两个黄球，三个白球
84“太阳每天从东方升起”，这是一个 事件（填“确定”或“不确定”）．确定
85．将正面分别标有数字6，7，8，背面花色相同的三张卡片洗匀后，背面朝上放在桌面上．
（1）随机地抽取一张，求(偶数)；
（2）随机地抽取一张作为个位上的数字（不放回），再抽取一张作为十位上的数字，能组成哪些两位数？恰好为“68”的概率是多少？
（1）
（2）能组成的两位数为：86，76，87，67，68，78
恰好为“68”的概率为．
86.A、B两个口袋中均有3个分别标有数字1、2、3的相同的球，甲、乙两人进行玩球游戏．游戏规则是：甲从A袋中随机摸一个球，乙从B袋中随机摸一个球，当两个球上所标数字之 和为奇数时，则甲赢，否则乙赢．问这个游戏公平吗?为什么?
解：不公平
下面列举所有可能出现的结果：
 |
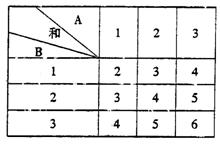由此可知，和为奇数有4种，和为偶数有5种
∴甲赢的概率为4/9，乙赢的概率为5/9
∴不公平
87 锦州市住宅电话号码是由7位数字组成，某人到电信公司申请安装一部住宅电话，那么该公司配送给这部电话的号码末尾数字为6的概率是____. 
88. 甲、乙两队进行拔河比赛，裁判员让两队队长用“石头、剪子、布”的手势方式选择场地位置.规则是：石头胜剪子，剪子胜布，布胜石头，手势相同再决胜负.请你说明裁判员的这种作法对甲、乙双方是否公平，为什么？(用树状图或列表法解答)
解：裁判员的这种作法对甲、乙双方是公平的.
理由：方法一：用列表法得出所有可能的结果如下：
| 甲 | 乙 | ||
| 石头 | 剪子 | 布 | |
| 石头 | (石头，石头) | (石头，剪子) | (石头，布) |
| 剪子 | (剪子，石头) | (剪子，剪子) | (剪子，布) |
| 布 | (布，石头) | (布，剪子) | (布，布) |
根据表格得，P(甲获胜)=，P(乙获胜）=
∵P(甲获胜)=P(乙获胜)，
∴裁判员这种作法对甲、乙双方是公平的.
方法二：用树状图得出所有可能的结果如下：
根据树状图，P(甲获胜)=，P(乙获胜）=.
∵P(甲获胜)=P(乙获胜)，
∴裁判员这种作法对甲、乙双方是公平的.
89．有四张背面相同的纸牌A，B，C，D，其正面分别划有四个不同的稽核图形（如图）．小华将这4张纸牌背面朝上洗匀后摸出一张，放回洗匀后再摸出一张．
（1）用树状图（或列表法）表示两次模牌
所有可能出现的结果（纸牌可用A、
B、C、D表示）；
（2）求摸出两张牌面图形都是中心对称
图形的纸牌的概率．
|
第一次摸的牌
第二次摸的牌
（列表略）
（2）
90.（课改）现有A、B两枚均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6）.用小莉掷A立方体朝上的数字为、小明掷B立方体朝上的数字为来确定点P（），那么它们各掷一次所确定的点P落在已知抛物线上的概率为（ ）
A. B.
C.
D.
91. 北京08奥运会吉祥物是“贝贝、晶晶、欢欢、迎迎、妮妮”.现将三张分别印有“欢欢、迎迎、妮妮”这三个吉祥物图案的卡片(卡片的形状大小一样，质地相同)放入盒子．
(1)小玲从盒子中任取一张,取到卡片欢欢的概率是多少?
(2)小玲从盒子中取出一张卡片,记下名字后放回,再从盒子中取出第二张卡片,记下名字.用列表或画树状图列出小玲取到的卡片的所有可能情况,并求出两次都取到卡片欢欢的概率．
（１）；
（２）列对表格或画对树状图；
两次都取到欢欢的概率为．