中考数学模拟试卷
考试说明：
1、 本试卷分为A卷和第B卷两部分，共30个小题，满分150分，考试时间120分钟.
2、 A卷分为第Ⅰ卷和第Ⅱ卷两部分，答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目准确填涂在答题卡上，请注意答题卡的横竖格式.
3、 第Ⅰ卷选择题共15个小题，选出答案后用铅笔把答题卡上对应题目的答案标号涂黑，若需改动，用橡皮擦擦干净后，再选涂其它答案，不准答在试卷上.
4、 第Ⅱ卷共6个小题，B卷共9个小题，用钢笔或圆珠笔直接答在试卷上，答题前将密封线内的项目填写清楚.
A卷（100分）
第Ⅰ卷 选择题（60分）
一、择题题（每小题4分，在给出的四个选项中，只有一项是符合题目要求的.）
1．
的相反数是（ ）
A.－2 B.2 C.－4 D.4
2．半径为4和8的两圆相内切，则圆心距为（ ）
A.4 B.8 C.12 D.16
3．下列多边形中，既是中心对称，又是轴对称的是（ ）
A.正三角形 B.正方形 C.正五边形 D.等腰梯形
4．下列事件中，属于确定事件的是（ ）
①向上抛出的篮球必然下落；②绵阳的冬天要下雪；③从一幅扑克牌中任意抽取7 张，至少有两张同花色；④抛两枚均匀的正方体骰子，正面朝上的两数之和大于1。
A.①②③④ B.①③④ C.①③ D.①④
5．一次函数y＝kx + b经过第二、三、四象限，则下列正确的是（ ）
A. k＞0，b＞0 B. k＞0，b＜0 C. k＜0，b＞0 D. k＜0，b＜0
6．点P（2，－6）和点Q（a，6）的连线垂直于x轴，则a的值为（ ）
A.－2 B.2 C.－6 D.6
7．一个正多边形，它的每一个外角都是45°，则该正多边形是（ ）
A.正六边形 B.正七边形 C.正八边形 D.正九边形
8．中央电视台3套“快乐中国行”栏目将从发送手机短信的10000名观众中抽取4名幸 运 观众，小李成功发送了一次手机短信，那么小李被抽中的机会是（ ）
A.
B.
C.
D. 
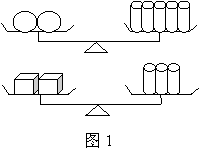
9．中央电视台2套“开心辞典”栏目中，一期的题目如图1所示，两个天平都平衡，则三个球体的重量等于（ ）个正方体的重量.
A.2 B.3 C.4 D.5
10．在Rt△ABC中，∠C＝90°，Sin A＝
，则cotB＝（ ）
A.
B. C.
D. 
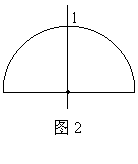
11．如图2所示，将一个量角器绕着直线l旋转180°，得到的图形是（ ）
A.球体 B.半球体 C.圆 D.不规则图形
12．已知反比例函数y＝
( k＜0)图象上有三点（x1，y1）、（x2，y2）、（x3，y3），且x1＜x2＜0＜x3，则下列正确的是（ ）
A.y1＞y2＞0＞y3； B.y2＞y1＞0＞y3； C.y3＞0＞y1＞y2； D.y3＞0＞y2＞y1
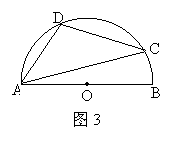
13．如图3所示，AB为⊙O的直径，C、D是⊙O上的两点，∠BAC＝20°，弧AD＝弧CD， 则∠DAC的度数为（ ）
A.30° B.35° C.45° D.70°
14．二次函数y＝x2－3x+6的顶点坐标是（ ）
A.（－3，6） B.（3，6） C.
D.
15．若二次函数y＝ax2+bx+c经过原点和第一、二、三象限，则（ ）
A. a＞0，b＞0，c＝0 B. a＞0，b＜0，c＝0
C. a＜0，b＞0，c＝0 D. a＜0，b＜0，c＝0
第Ⅱ卷（非选择题，40分）
二、解答题：本大题6小题，解答时应写出必要的文字说明，证明过程或演算步骤.
16．(本题满分6分)计算：
；
17．(本题满分6分)因式分解：a2x2－4+a2y2－2a2xy；
18．(本题满分6分)
如图4所示，△ABC中，AB＝5，AC＝4，BC＝3，点D是AB上的一个动点，∠B＝∠EDC，
，设CD＝x，△EDC的周长为y，求y与x的函数关系式，并求自变量的取值范围.
19．(本题满分6分) 暑假某班学生租船游览三江，码头还剩下几只船可租用，如果每船坐6人，则余下18人无船可坐；如果每船坐10人，则有船不空也不满.试计算码头剩有几只船及学生总人数.
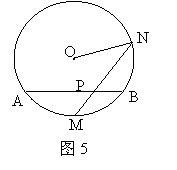
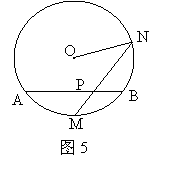20．(本题满分8分)如图5所示，已知⊙O的直径为4cm，M是弧的中点，从M作弦MN，且MN＝
cm，MN交AB于点P，求∠APM的度数.
21．(本题满分8分)某公司欲招聘业务员一名，现对A、B、C三名候选人分别进行三项素质测试，成绩如下表：
| 测试项目 | 测 试 成 绩 | ||
| A | B | C | |
| 创 新 | 72 | 85 | 67 |
| 综合知识 | 50 | 74 | 70 |
| 语 言 | 88 | 45 | 67 |
（1）如果按照三人测试成绩的平均成绩录取人选，那么谁将被录用？
（2）根据实际需要，公司将创新、综合知识和语言三项成绩按5:4:1的比例确定各人的测试成绩，此时谁将被录用？
B卷（50分）
三、填空题：本大题共6小题，每小题3分，共18分. 将答案填写在对应题号的横线上.
22．当x 时，代数式
有意义.
23．如图6所示，AB是⊙O的直径，弦CD与AB交于点E，若 ，则CE＝CD（只需添加一个你认为适当的条件）
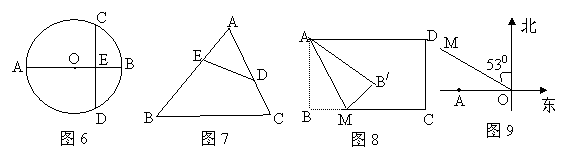
24．如图7所示，DE与BC不平行，请你添加一个条件，使△ADE与△ABC相似，你添加的条件是 .
25．一次函数y＝x－4与反比例函数
的交点坐标是 .
26．若不等式4x－a≤0的正整数解恰为1、2、3，则a的取值范围是 .
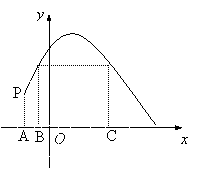
27．如图8所示，一张长方形纸片ABCD，其长AD为a，宽AB为b（a＞b），在BC边上任取一点M，将△ABM沿AM翻折后B到B＇后置，若B＇恰为AC的中点，则
.
四、解答题：本大题共3小题，共29分，解答时应写出必要的文字说明，证明过程或演算步骤.
28．(本题满分10分)如图9，某校的教室A位于工地O的正西方，且OA＝200m，一辆拖拉机从O点出发，以每秒5m的速度沿北偏东53°方向OM行驶，设拖拉机周围130m均受其噪音污染，试问教室A是否在拖拉机的噪音污染范围之内？若不在，说明理由；若在，求教室A受拖拉机的噪音污染的时间是多少？（供选用数据：Sin53°＝0.80 Sin37°＝0.60 tan37°＝0.75）.
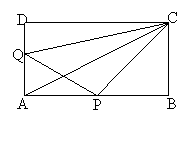
29．(本题满分10分)一名篮球运动员传球，球沿抛物线y＝－x2+2x+4运行，传球时，球的出手点P的高度为1.8米，一名防守队员正好处在抛物线所在的平面内，他原地竖直起跳的最大高度为3.2米，
问：（1）球在下落过程中，防守队员原地竖直起跳后在到达最大高度时刚好将球断掉，那么传球时，两人相距多少米？
（2）要使球在运行过程中不断防守队员断掉，且仍按抛物线y＝－x2+2x+4运行，那么两人间的距离应在什么范围内？（结果保留根号）
30．阅读材料，回答问题(本题满分12分)
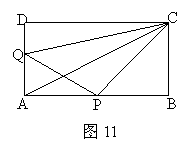
如图，在矩形ABCD中，AB＝12cm，BC＝6cm，点P沿AB边从A向B以2cm/s的速度移动；点Q沿DA边从D向A以1cm/s的速度移动.如果P、Q同时出发，用t（s）表示移动时间（0≤t≤6），那么：（1）当t为何值时，△QAP为等腰直角三角形？（2）求四边形QAPC的面积；你有什么发现？（3）当t为何值时，以点A、P、Q为顶点的三角形与△ABC相似？
[参考答案]
一、择题题（每小题4分，在给出的四个选项中，只有一项是符合题目要求的.）
1.B 2.A
3.B 4.B 5.D
6.B 7.C 8.C
9.D 10.D
11.B 12.B 13.B 14.D 15.A
二、解答题：
16.原式=
……..……….2分
=
………………4分
=
=-3 ………………6分
17.a2x2－4+a2y2－2a2xy
=（a2x2－2a2xy+a2y2）－4 …………………2分
= a2（x2－2xy+y2）－4
= a2（x-y）2－22 ………………4分
=( a x -ay+2）( a x –ay-2） ………………6分
18.∵∠B＝∠EDC，
∴△ABC∽△EDC ………..2分
∵AB＝5，AC＝4，BC＝3，CD＝x，
∴
，
，
∴
……….4分
∵AB＝5，AC＝4，BC＝3，
∴∠C＝900，∴
≤CD≤4，即≤x≤4 …….6分
19.解：设码头剩有x只船，则学生有（6x+18）人，由题可得：………1分
10（x+1）＜6x+18＜10x
…………3分
解得：4.5＜ x ＜7，
∵x只能为整数，∴x=5或6 …………4分
当x=5时，6x+18=48；
当x=6时，6x+18=54. …………5分
20.连结OM交AB于点E，
∵M是弧的中点，∴OM⊥AB于E，…………….2分
过点O作OF⊥MN于F，
由垂径定理得：
，…………….4分
在Rt△OFM中，OM=2，
，
∴cos∠OMF= 
，
……………6分
∴∠OMF=300，
∴∠APM=600 …………8分
21.解：（1）A的平均成绩为
（分） ……………….1分
B的平均成绩为
（分） ……………….2分
C的平均成绩为
（分） ……………….3分
所以A将被录用.
……………….4分
（2）A的测试成绩为
（分）……………….5分
B的测试成绩为
（分） ……………….6分
C的测试成绩为
（分） ……………….7分
所以B将被录用.
……………….8分
三、填空
22.x＞1且x≠3
23.CD⊥AB或弧BC=弧BD或B是弧CD的中点.
24.∴∠ADE=∠B或∠AED=∠C或
.
25.：
或
26.9≤a＜16.
27.连结BB/、AC，∵B＇为AC的中点，
∴AB＇=C B＇，∵AB＇=AB，∴△AB B＇为等边三角形，
∵∠ABC=900 ，∴∠ACB=300 ，
∴
.
四、解答题
28.解：过点A作AB⊥OM于B ， …………….1分
∴∠AOB=370，∵OA=200米，∴AB=200×sin370=200×0.6=120（米） …………3分
∵120＜130，∴教室A会受到拖拉机的噪音污染.. …………4分
以A为圆心、130米为半径画圆，交OM于点C、D两点， ……………6分
∵AB=120米，AC=AD=130米，∴BC=BD=50米，CD=100米， ……………8分
∴100÷5=20（秒）即教室A受到拖拉机的噪音污染.的时间是20秒. …………9分
答：教室A会受到拖拉机的噪音污染.，受到污染.的时间是20秒.…………10分
29.解：当y=1.8米时则有：
，
∴
，解得：
，
，
当y=3.2米时则有：
，∴
，
解得：
，
，所以两人的距离为：
AC=
=
.
（2）由（1）可知：当y=1.8米时，有，，
当y=3.2时，有，，
∴ 
，
，
∴
，∴两人之间的距离在
到之间.
30.（1）对于任意时刻的t有：AP=2t，DQ=t，AQ=6-t，
当AQ=AP时，△AQP为等腰直角三角形 ……2分
即6-t=2t，∴t=2，
∴ 当t=2时，△QAP为等腰直角三角形. ……4分
（2）在△AQC中，AQ=6-t，AQ边上的高CD=12，
∴S△AQC=
在△APC中，AP=2t，AP边上的高CB=6，
∴S△APC=
………6分
∴四边形QAPC的面积SQAPC= S△AQC +S△APC=36-6t+6t=36（cm2）
经计算发现：点P、Q在运动的过程中，四边形QAPC的面积保持不变.………8分
（3）根据题意，应分两种情况来研究：
①当
时，△QAP∽△ABC，则有
，求得t=1.2（秒）………9分
②当
时，△PAQ∽△ABC，则有
，求得t=3（秒） ………11分
∴当t=1.2或3秒时，以点A、P、Q为顶点的三角形与△ABC相似. ………12分
 |