中考数学开放探索性专题测试题
（满分：100分；考试时间：100分钟）
| 题号 | 一 | 二 | 三 | 总分 | ||||||
| 16 | 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得分 | ||||||||||
一、填空题（每小题3分，共24分）
1. 在四边形ABCD中，已知AB//CD，请补充条件 （写一个即可），使得四边形ABCD为平行四边形；若ABCD是平行四边形，请补充条件 (写一个即可)，使四边形ABCD为菱形。
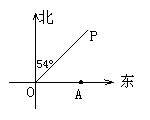
2. 如图1，某校为扩大高中招生，正在施工增盖教学楼，一推土机沿北偏东54°方向的OP工地线来回推土，它的噪声对位于O点正东方向200米处的一教室A已造成影响，当推土机的距O点 米处时，推土机的噪声对教室A影响最大。
（1） （2） （3）
3. 在△ABC和△ADC中，下列三个论断：①AB=AD；②∠BAC＝∠DAC；③BC=DC将其中的两个论断作为条件，另一个论断作为结论写出一个真命题是 。
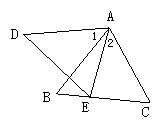
4. 如图2，已知∠1=∠2，若再增加一个条件就能使结论“AB·DE=AD·BC”成立，则这个条件可以是 。
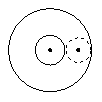
5. 如图3，这是一个滚珠轴承的平面示意图，若该滚珠轴承的内、外圆周的半径分别为2和6，则在该轴承内最多能放 颗半径均为2的滚珠。
6. 观察下列算式并填空：32-12=8×1，52-32=8×2。
①72-52=8× ；②92- 2=8×4;③ 2-92=8×5；④132- 2=8×6，
……
通过观察归纳，写出反映这种规律的一般结论： _____________ （用文字语言表述）。
7. 用计算器探索：按一定规律排列的一组数：
1，
，-
，2，
，-
，
……，如果从1开始依次连续选取若干个数，使它们的和大于5，那么至少要选 个数。
8. 根据指令[S，A]（S≥0，0°＜A＜180°），机器人在平面上能完成下列动作：先原地逆时针旋转角度A，再朝其面对的方向沿直线行走距离S，现机器人在直角坐标系的坐标原点，且面对y轴正方向。（1）若给机器人下了一个指令[4，60°]，则机器人应移动到点 ；（2）请你给机器人下一个指令 ，使其移动到点（-5，5）。
二、选择题（每小题3分，共21分，每小题只有一个答案正确，请把正确答案的代号填入题后的括号内）。
9. 用两块完全重合的等腰直角三角形纸片拼成下列图形：①平行四边形（不包含菱形、矩形、正方形）；②矩形；③正方形；④等边三角形；⑤等腰直角三角形，其中一定能拼成的图形是（ ）
A. ①②③ B. ②③⑤ C. ①③⑤ D. ①③④⑤
10. 在Rt△ABC的直角边AC上有一点P（点P与点A、C不重合），过点P作直线截△ABC，使截得的三角形与△ABC相似，则满足条件的直线共有（ ）
A. 4条 B. 3条 C. 2条 D. 1条
11. 若二次函数y=ax2+c，当x取x1，x2(x1≠x2)时，函数值相等，那么当x取x1+x2时，函数值是（ ）
A. a+c B. a-c C. –c D. c
12. 圆内接四边形ABCD中，由AB//DC不一定能推出（ ）
A. AD=BC B.
AC=BD C.
D. AD//BC
13. 在共有15人参加的“我爱祖国——争做五小公民”演讲比赛中，参赛选手成绩各不相等，因此选手要想知道自己是否进入前8名，只需要了解自己的成绩以及全部成绩的（ ）
A. 平均数 B. 众数
C. 中位数 D. 方差
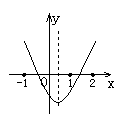
14. 二次函数y=ax2+bx+c的图象如图所示，则a、b、c、a+b+c这四个式子中，值为正数的有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
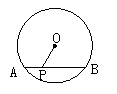
15. 如图4，⊙O的直径为10cm，弦AB为6cm，P是弦AB上一点，若OP的长为整数，则满足条件的点P有（ ）
A. 2个 B. 3个 C. 4个 D. 5个
（4） （5）
三、解答题。（共55分）
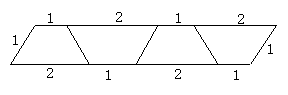
16. （6分）如图5，观察由梯形拼成的图形和所给表样中的数据后回答问题。
| 梯形个数 | 1 | 2 | 3 | 4 | 5 | …… |
| 图形周长 | 5 | 8 | 11 | 14 | 17 | …… |
（1）当梯形的个数为10个时，图形的周长是 ；
（2）当梯形的个数为n时，求图形的周长（用含n的代数式表示），并求当图形的周长为80时，梯形的个数。
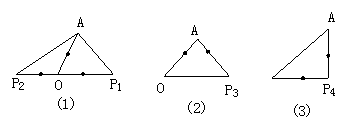
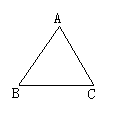
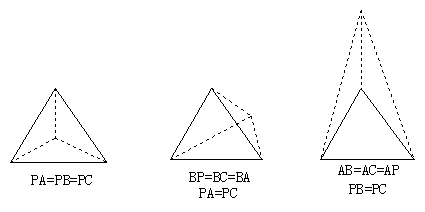
17. （6分）△ABC是等边三角形，找一点P使△PAB、△PAC、△PBC都是等腰三角形，请分别在下列三个图形中画出点P的位置，并分别注明哪些线段相等。
18. （7分）在平面直角坐标系中，已知点A（1，6），B（2，3），C（3，2）。
（1）在平面直角坐标系中描出点A、B、C；
（2）根据你学过的函数类型，推测这三个点会同时在哪种函数的图象上；
（3）求出（2）中你推测的函数图象的解析式，并说明该函数的图象一定过这三个点。
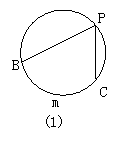
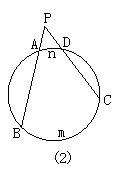
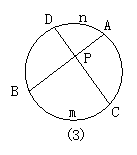
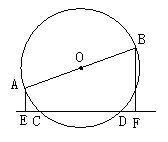
19. （8分）如图，点P在圆上，依据圆周角定理可知：∠BPC等于
度数的一半，分别考察图（2）、（3）两种情形；当点P在圆外（或圆内）时，BP、CP （或它们的延长线）分别交圆于A、D，设的度数是x，
的度数是y，试用x、y表示∠BPC的大小，并说明你的结论。
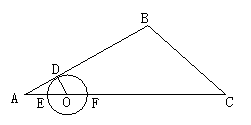
20. (8分)已知：如图，在△ABC中，AC=14，BC=6 ，∠ACB=45°，点O在AC边上移动，以O为圆心作⊙O，使⊙O与AB相切，切点为D，⊙O与AC边交于E、F两点（点E在点F左边）。设⊙O的半径为r，四边形BDOC的面积为S。求：S与r的函数关系式。
21. （8分）如图所示，AB是⊙O的直径，直线EF与⊙O相交于C、D，AE⊥EF于E，BF⊥EF于F，在线段EF上是否存在点P，使得以P、A、E为顶点的三角形和以P、B、F为顶点的三角形相似？若不存在，说明理由；若存在，这样的点P共有几个？并指出点P在图形中的位置。
22. （12分）已知反比例函数y=
和一次函数y=2x-1，其中一次函数的图象经过（a，b），(a+1，b+k)两点。
（1）求反比例函数的解析式； （2）如图，已知点A在第一象限，且同时在上述两个函数的图象上，求A点坐标；
（3）利用（2）的结果，请问：在x轴上是否存在点P，使△AOP为等腰三角形？若存在，把符合条件的P点坐标都求出来；若不存在，请说明理由。
 |
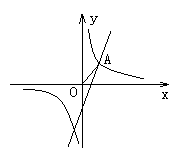答案
一、填空题
1. AB=CD等 AB=BC等。
2. 162。
3. ①② →③。
4.∠B=∠D 或者∠AED=∠C等。
5. 6。
6. 3；7；11；11；两个连续奇数的平方差能被8整除（或是8的倍数）。
7. 7。
8. (-2，2)；[5，45°]
二、选择题
9. C；10. B；11. D；12. D；13. C；14. A；15. B。
16. （1）32；（2）5+3（n-1）或2+3n，n=26。
17.
18. （1）略；
（2）反比例函数图象上；
（3）
19. 图②中，连结BD可得∠BPC=∠BDC-∠ABD
=
图③中，连结BD，可得∠BPC=∠BDC+∠ABD=
20. 过B作BH⊥AC于H，可求得S=-
21. 连结AD、BC、AC、BD则△ACE△CBF，△AED∽△DFB，由此可知满足条件的点P有C、D两个。
22. （1）y=
；
（2）A（1，1）；
（3）①当OA为腰时，由OA=OP得
P1=（，0），P2（-，0）（如图①）
②当OA=AP，得P3（2，0）（如图②）
③当OA为底时，得P4（1，0）（如图③）
故符合条件的点有4个，分别是（，0），（-，0），（2，0）（1，0）
