中考数学探索性专题单元测试题

中考数学探索性专题单元测试题

（满分：100分；考试时间：100分钟）　

一、填空（每小题5分，共50分）

1. 观察：2¹=2，2²=4，2³=8，2⁴=16，2⁵=32，2⁶=64，2⁷=128，2⁸=256…

通过观察用你所发现的规律写出2¹⁹⁹⁵的未位数是　　　　　　　　　 。

2. 瑞士中学教师巴尔米成功地从光谱数据、、、…中得到巴尔

米公式，从而打开了光谱奥妙的大门，请你按这种规律写出第七个数　　　 。

3. 下列是一个有规律排列的数表：

　　　　  第1列　 第2列　　第3列　　第4列…第n例…

　第1行：　　　　　　　　　　　　　　…　…

　第2行：　　　　　　　　 　　　　　…　…

第3行：　　　　　　　　　　　　　　…　…

上面数表中第9行，第7列的数是　　　　　　 。

4. 观察下面一列数：　　　　1

　　　　　　　　　　 -2　　3　 -4

　　　　　　　　　　 5　 -6　　7　　-8　　9

　　　　　　　 -10　 11　-12　 13　 -14　 15　 -16

　　　　　　 　　 ……　 ……

按上述规律排下去，那么第10行从左边数第9个数是　　　　 。

列 行	一	二	三	四	五
一		1	3	5	7
二	15	13	11	9
三		17	19	21	23
四	…	…	27	25

5. 将正奇数如下表排列：　　　　　　　　　　　　　　　　　　　　 

按表中的排列规则，数　　　　　　　　　　　　　　　　　　　　　　

2005应排在第　 行第　 列。 　　　　　　　　　　　　　　　　　　　

6. 已知n（n≥2）个点P₁、P₂、P₃…P_n在同一平面内，且其中没有任何三点在同一直线上，设Sn表示过这n个点中的任意2个点所作的所有直线的条数，显然S₂=1，S₃=3，S₄=6，S₅=10…，由此推断S_n=　　　　　　　 。

7. 如图，摆第1个“小屋子”要5枚棋子，摆第二个要11枚棋子，摆第3个要17枚棋子，则摆第30个“小屋子”要　　　 枚棋子。

 

　　　　　　　  （1）　　　　（2）　　　　　 （3）

8. 用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案，则第n个图案需要用白色棋子　　　　　　 枚（用含有n的代数式表示）。

○ ○ ○　　　 ○ ○ ○ ○　　　○ ○ ○ ○ ○

　　　　　　　 ○ ● ● ○　　  ○ ● ● ● ○

○ ● ○　　　 ○ ● ● ○　　　○ ● ● ● ○

　　　　　　　 ○ ○ ○ ○　　  ○ ● ● ● ○

○ ○ ○　　　 　　　　　　　　 ○ ○ ○ ○ ○

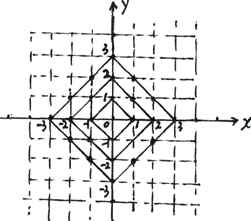
9. 在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点，观察图中每一个正方形（实线）四条边上的整点的个数，请你猜测由里向外第10个正方形（实线）四条边上的整点个数共有　　　　 个。

10. 在数学活动中，小明为了求++++…+的值（结果用n表示），设计如图1所示的几何图形。

　（1）请你利用这个几何图形求++++…+的值为　　　　。

　（2）请你利用图2，再设计一个能求++++…+的值的几何图形。

　　　　　　

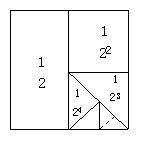
　　　　　　　　  （1）　　　　　　　　　　　　　　 （2）

二、解答下列各题（每小题10分，共50分）

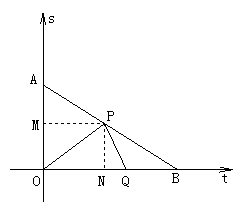
　11. 已知，Rt△AOB中，∠AOB=90°，OA=3cm，OB=4cm，以O为坐标原点建立如图所示的平面直角坐标系，设P、Q分别为AB边、OB边上的动点，它们同时分别从点A、O向B点匀速运动，移动的速度为1cm/s，设P、Q移动时间为ts（0≤t≤4）。

　（1）过点P作PM⊥OA于M，证明，

并求出点P的坐标（用t表示）。

　（2）求△OPQ的面积S（cm²）与移动时间t（s）之间的函数关系式；当t为何值时，S有最大值，并求出S的最大值。

　（3）请你探索：当t为何值时，△OPQ为直角三角形。

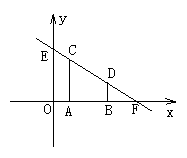
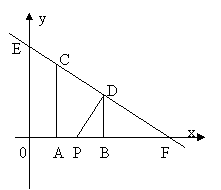
　12. 如图，在平面直角坐标系中，CA⊥x轴于点A（1，0），DB⊥x轴于点B（3，0），直线CD与x轴、y轴分别交于点F、E，S_{四边形ABDC}=4。

　（1）若直线CD的解析式为y=kx+3，求k的值；

（2）试探索在x轴正半轴上存在几个点P，使△EPF为等腰三角形，并求出这些点的坐标。

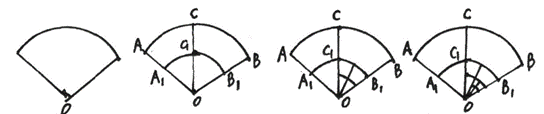
13. 下图中，图（1）是一个扇形AOB，将其作如下划分：

第一次划分：如图（2）所示，以OA的一半OA₁为半径画弧，再作∠AOB的平分线，得到扇形的总数为6个，分别为：扇形AOB，扇形AOC，扇形COB，扇形A₁OB₁，扇形A₁OC₁，扇形C₁OB₁；

第二次划分：如图（3）所示，在扇形C₁OB₁中，按上述划分方式继续划分，可以得到扇形的总数为11个；

第三次划分：如图（4）所示：…依次划分下去。

　　　　 （1）　　　　　  （2）　　　　　　　  (3)　　　　　　　  (4)

（1）根据题意，完成下表：

划分次数	扇形总个数
1	6
2	11
3
4
…	…
n

　（2）根据上表，请你判断按上述划分方式，能否得到扇形的总数为2005个？为什么？

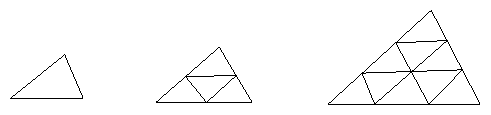
　14. 下列各图是由小三角形拼凑而成的图形。

　　　　 (1)　　　　　　　　　　 (2)　　　　　　　　　　　　 (3)

　（1）请观察每一个图形中小三角形的个数，并完成下表：

层数n	1	2	3	4	5	…
小三角形的总数m						…

　（2）根据上表中的数据，把n作为横坐标，把小三角形的总数m作为纵坐标，在平面直角坐标系中描出相应的各点（n，m）其中1≤n≤5；

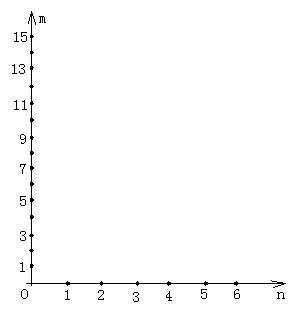
　（3）请你猜一猜，上述各点会在某一函数图象上吗？如果在某一函数的图象上，请写出该函数的表达式。

　15. 已知抛物线y=x²+(2n-1)x+n²-1（n为常数）

　（1）当该抛物线经过坐标原点，并且顶点在第四象限时，求出它所对应的函数关系式；

（2）设A是（1）所确定的抛物线上的一个动点，它位于x轴下方，且在对称轴左侧，过A作x轴的平行线，交抛物线于另一点D，再作AB⊥x轴于B，DC⊥x轴于C；

①当BC=1时，求矩形ABCD的周长；

②试问矩形ABCD的周长是否存在最大值？如果存在，请求出这个最大值，并指出此时A点的坐标；如果不存在，请说明理由。

参考解答

一、填空题

（1）8；（2）；（3）；（4）90°；（5）251，4；（6）；（7）179；

（8）4n+4（或4（n+1）或4（n+2）-4或（n+2）²-n²）；（9）40；（10）①1-

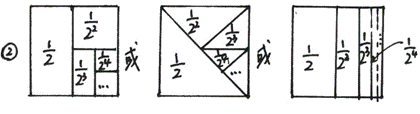
二、11. ①作PN⊥OB，OB⊥OA

∵PM⊥OA，OB⊥OA　　

∴PM∥BO　　

∴△AMP∽△AOB

∴

又∵OA=3，OB=4　　　　

∴AB==5

又∵AP=1×t=t

∴　　　

∴AM=t，

∴PM=t

∴PN=OM=OA-AM=3-t　　

∴P点坐标为（t，3-t）

②S△OPQ=OQ·PN=t·（3-t）=-t²+t=-（t-）²+

∴当t=s时，S有最大值为cm²

③在△OPQ中，∠POQ＜90°，∠POQ＜90°，

要使△OPQ为Rt△，只能∠OPQ=90°，

若Rt△PNO∽Rt△QNP，可得∠OPQ=90°，

只要，即PN²=ON·NQ，

可证Rt△PNO∽Rt△QNP。

　　∵PN=3-t，ON=PM=t，NQ=OQ-ON=t-t=t

∴（3-t）²=t·t　　

∴t₁=3，t₂=15（不合题意，舍去）

即当t=3（S）时，△OPQ为Rt△。

12. (1)∵A（1，0）　B（3，0）　 ∴AB=2

∵S_{四边形ABCD}=（AC+BD）×2=4

∴AC+BD=4

设C（1，y₁）， D（3，y₂）

∵y=kx+3， ∴y₁=k+3，y₂=3k+3

∴y₁+y₂=4k+6即4k+6=4，得k=-

（2）有2个①当点P在线段OF上时，

在y=-x+3中，令y=0得x=6

∴F（6，0）

∴B（3，0）是线段OF的中点，

∴D为线段EF的中点

过点D作EF的垂线DP交x轴于点P，则点P为满足条件的点。

∵Rt△PDB∽Rt△DFB　　∴PB=

在直线CD的解析式y=-x+3中，令x=3，得y=，即DB=

又BF=3，∴PB=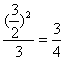　　

∴OP=OB-PB=3-

∴点P（，0）

②当点P在点F右边时，∵FP=EF=

∴OP=OF+FP=6+3　 此时P（6+3，0）

　13. (1)16，21，……5n+1

　（2）不能够得到2005个扇形，

因为满足5n+1=2005的正整数n不存在。

　14. (1)1，4，9，16，25

（2）略

（3）m=n²

　15. （1）y=x²-3x　

（2）①矩形周长为6　

②当x=时，矩形周长最大值为。