中考数学数与式复习
第1课 实数的有关概念
目的：复习实数有关概念，相反数、绝对值、倒数、数轴、非负数性质、科学记数法、近似数与有效数字．
中考基础知识
1．实数的分类
2．相反数：只有_______不同的两个数，叫做互为相反数，a的相反数为______，a-b的相反数是_______，x+y的相反数是________，0的相反数为_______，若a，b互为相反数，则a+b=________．
3．绝对值：几何意义：数a的绝对值是数a在数轴上表示的点到_______的距离．
正数的绝对值等于它________．
代数意义 零的绝对值等于________．
负数的绝对值等于它的________．
│a│=
4．数轴：
________与数轴上的点是一一对应的，数轴上的点表示的数左边的总比右边的_________，数轴是沟通几何与代数的桥梁．
5．倒数：a（a≠0）的倒数为________，0_______倒数，若a，b互为倒数，则ab=_____，若a，b互为负倒数，则ab=________．
6．非负数：│a│≥0，a2≥0，
≥0．
若│a+1│+
+（c+3）2=0，则a=_______，b=_______，c=________．
7．科学记数法：把一个数记作a×10n形式（其中a是具有一位整数的小数，n为自然数）．
8．近似数与有效数字：一个经过________而得到的近似数，最后一个数在哪一位，就说这个近似数是精确到哪一位的近似数，对于一个近似数，从左边第一个______数字开始，到最末一位数字止，都是这个近似数的有效数字．
备考例题指导
例1．填空题
（1）
-2的倒数为_______，绝对值为________，相反数为_______．
（2）若│x-1│=1-x，则x的取值范围是_______，若3x+1有倒数，则x的取值范围是_________．
（3）在实数-
，18，
，
，0，
+1，0.303003……中，无理数有________个．
（4）绝对值不大于3的非负整数有________．
（5）若
=0，则3x-2y=________．
（6）用科学记数法表示-168000=_______，0.=_________．
（7）0.0304精确到千分位等于_______，有_______个有效数字，它们是_______．
（8）保留两个有效数字得到的近似数为________．
答案：（1）．--2，2-，2-
（2）x≤1，x≠-
． （3）5． （4）0，1，2，3．
（5）7． （6）-1.68×105，2.004×10-4．
（7）0.030；2；3，0 （8）2.1×106．
例2．已知1<x<4，化简│x-4│-
．
解：∵1<x<4， ∴x-4<0，1-x<0．
原式=│x-4│-│1-x│=4-x+1-x=5-2x．
例3．化简│x-2│+│x+3│．
解：令x-2=0得x=2，令x+3=0得x=-3．
（1）当x<-3时，原式=2-x-x-3=-2x-1；
（2）当-3≤x<2时，原式=2-x+x+3=5；
（3）当x≥2时，原式=x-2x+x+3=2x+1．
分类讨论思想，零点分段法，一般等号取在大于符号中．
备考巩固练习
1．一个数的相反数是3，则这个数是________．
2．气温比a℃低3℃记作________．
3．若（-a）2与│b-1│互为相反数，则
的值为_______．
4．若a2+2a+1+
+│c-2003│=0，则ab+c=________．
5．计算
-
+
-
-
-
=______________．（注意方法）
6．计算│1-a│+│2a+1│+│a│，其中a<-2．
7．如果表示a、b两个实数的点在数轴上的位置如图，那么化简│a+b│+
的结果是多少？
8．按要求取下列各数的近似数：
（1）6.286（精确到0.1）；（2）（保留三个有效数字）；（3）278160（精确到万位）．
9．近似数7.60×105精确到_______位，有______个有效数字，近似数7.6×105精确到_______位，有________个有效数字．
10．已知a、b、c为实数，且a2+b2+c2=ab+bc+ac，求证a=b=c．
答案:
1．-3 2．（a-3）℃
3．+1 4．2004
5．原式=-+-+-=
-1+1
=（先去绝对值符号）
6．∵a<-2，∴1-a>0，2a+1<0，a<0
∴原式=1-a-2a-1-a=-4a
7．-2a
8．（1）6.286≈6.3 （2）≈1.76×106
（3）278160≈28万
9．∵7.60×105=760000 ∴近似数7.60×105精确到千位，有三个有效数字7，6，0；
7.6×105精确到万位，有两个有效数字7，6
10．用配方法和非负数性质，将一个方程转化为三个方程，a2+b2+c2-ab-bc+ac=0
2a2+2b2+2c2-2ab-2bc-2ac=0 （a-b）2+（b-c）2+（a-c）2=0
∴a-b=0，b-c=0，a-c=0 ∴a=b=c
第2课 实数的运算
目的：复习实数大小的比较，有理数的加、减、乘、除、乘方运算．
中考基础知识
1．有理数与小学所学数的运算有三大区别：
（1）1-6=-5（减不够倒过来减取负）
（2）-3-6=-9（连减当加算取负）
（3）-
×=-
，-×（-）=（同号得正，异号得负）
2．运算过程中充分利用运算律．
3．运算中一定要注意顺序和符号，否则会犯严重错误．
4．零指数幂和负整指数幂的运算法则：
a0=________，（a≠______）；a-p=（ ）p（a≠0）
5．特殊角三角函数值：
sin30°=_______，cos30°=_______，
tan30°=_______，cot30°=_______，
sin45°=_______，cos45°=_______，
tan45°=_______，cot45°=_______，
sin60°=_______，cos60°=_______，
tan60°=_______，cot60°=_______．
备考例题指导
例1．计算
3-2÷3+（-）0-3-1+（-3）2-32
解：原式=3-
+1-+9-9=3
在算3-2÷3时易算成1÷3=，另外（-3）2与-32是有区别的．
例2．计算：
（1-tan60°）（）-2-（-
）0
-0.252005×42005．
解：原式=（1-）×4-1-（0.25×4）2005
=4-4-1-1
=2-4．
例3．计算-12-（-2）×（-1）2004+（sin60°）-2+（2+）-1．
解：原式=1-（-2）×1+（
）-2+
=-1+2+
+2-
=
-．
注意符号，另外（）-2=（
）2=．
例4．比较大小：（1）-
与-； （2）-2与-3．
解：（1）∵-=-
，-=-
，
∴->-．
通分比较，绝对值大的负数反而小
（2）∵-2=-
，-3=-
，
∴-2>-3．
备考巩固练习
1．若（a-）2与│b-2│互为相反数，则
的值为_________．
2．比较大小：（1）（）-1，（+1）0，（-2）2：___________．
（2）0<x<1，比较x，
，
，x2的大小：________．
3．比较大小：（1）7与4：_________．
（2）
-
与3-：_________．
4．已知x2+y2+4x-6y+13=0，求yx的值．（提示：用配方法）．
5．计算下列各题：
（1）（-）×52÷-+（-）0 +（-2）2003 ·（+2）2004+tan60°;
（2）-0.52+-2--22-4-（-1）3×（-）3÷（-）4
（3）20032-2002×2004;
（4）
+（-1）0-2sin45°
（5）已知a2-12a+36+
+│c-9│=0，求
的值．
（6）（2003，山东）在一列数1，2，3，4…，100中，求数字“0”出现的次数．
（7）（2004，桂林）计算-+sin45°-（
-1）0
（8）计算：-23×2-1+ ÷（tan30°-cos45°）
答案:
1．由题知（a-）2+│b-2│=0，∴a=，b=2
∴=
=
=-2
2．（1）计算比较（）-1=5，（+1）0=1，（-2）2=4
∴（）-1>（-2）2>（+1）0
（2）特殊值法比较，取x=
计算
x=，=4，=，x2=
∴>>x>x2
3．（1）用平方法，72=49，（4）2=16×3=48
∴7>4
（2）用分子有理化法：-=
=
3-=
=
∵分子相同，3+>+
∴3-<-
4．由已知可知，x2+4x+4+y2-6y+9=0，（x+2）2+（y-3）2=0
∴x=-2，y=3，∴yx=3-2=
5．（1）原式=
×25÷+1+（-2）2003·（+2）2003·（+2）+．
=10+1--2+=9
（2）原式=-+-8+
÷
（3）原式=20032-（2003-1）（2003+1）=20032-20032+1=1
（4）原式=-1+1-2×
=0
（5）由等式知a=6，b=8，c=9
∴原式=
=
=1
（6）192次
（7）
（8）2-4
第3课 整式的加减
目的：复习整式的概念，去括号、添括号法则，求代数式的值，整式的加减运算．
中考基础知识
1．代数式的分类
代数式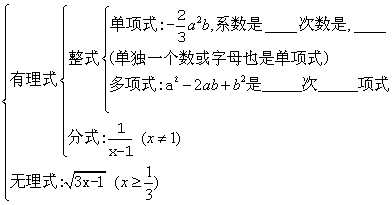
2．去括号添括号法则
a+（b-c）=a+b-c， a-（b+c）=a-b-c， a+b-c=+（ ）， a-b+c=-（ ）．
3．整式加减：实质上就是合并同类项．
备考例题指导
例1．代数式
是（ ）
（A）多项式 （B）分式 （C）无理式 （D）单项式
分析：在做这道选择题时，应注意“数”与“式”是有区别的，无理数的根号内不含有字母，它不是无理式，又题中虽有分母但分母中也不含有字母，所以它不是分式，因题中实质上是-
表示两个单项式的差，因此应该是多项式，故选（A）．
例2．比较a与-a的大小关系是（ ）
（A）a>-a （B）a≥-a （C）a<-a （D）以上答案都不对
分析：题中的a是实数，当a等于零时，（A）（C）答案都不成立，当a为负数时，（B）不成立，故应选（D）．
例3．单项式3xm+2ny4与-2x2y3m+4n是同类项，求nm的值．
分析：由同类项定义知：
转化为二元一次方程组，求出m，n，然后代入可求值．
答案：nm=1．
例4．先化简，再求值：（2a+1）2-（2a-1）（2a-1），其中a=
分析：对代数式进行化简时，应根据式子特点，合理使用公式，特别注意化简过程中的符号问题．
解：原式=（4a2+4a+1）-（4a2-1）
=4a+2．
当a=时，原式=4×+2=2．
备考巩固练习
1．填空题
（1）-
x3y2z的系数是________，次数是______，x-xy+1是______次_______项式．
（2）把a2b-4ab2+2a3b-1按a的降幂排列为___________．
（3）若x2m-1y2m与-x5yn+7是同类项，则（m-n）-1的值为_________．
（4）3x2-2x-1=3x2-（_________）;4a2-2ab+b2+1=4a2+（_________）．
（5）化简-3（2a+3b）-（6b-12a）=_________．
（6）合并同类项a-a-3c-2c-c=________．
（7）当x=-2时，代数式x2-2x+1的值为_________．
2．计算:
a2-[a2-（a2-2a）+2（a2-a）-a2]．
3．已知2x2+3x-6=A（x-1）2+B（x-1）+C，求实数A、B、C．
4．多项式8x2+2x-5减去另一个多项式的差是5x2-x+3，求另一个多项式．
5．已知A=5x2-mx+n，B=-3y2+2x-1，若A+B中不含有一次项和常数项，求m2-2mn+n2的值．
6．先化简，后求值：（a+b）（a-b）+b（b-2），其中a=，b=-1．
7．有一列数：第一个数为x1=1，第二个数为x2=3，第三个数开始依次记为x3，x4，…，xn；从第二个数开始，每个数是它相邻两个数和的一半．（如x2=
）
（1）求第三、第四、第五个数，并写出计算过程；
（2）根据（1）的结果，推测x8=_________．
（3）探索这一列数的规律，猜想第K个数Xk=_______．（K是大于2的整数）
答案:
1．（1），6，二次三项式
（2）原式=2a3b+a2b-4ab2-1
（3）由题知
∴（m-n）-1=
（4）3x2-2x-1=3x2-（2x+1），
4a2-2ab+b2+1=4a2+（-2ab+b2+1）
（5）原式=-6a-9b-2b+4a=-2a-11b
（6）原式=-a-6c
（7）原式=（x-1）2=（-2-1）2=（-3）2=9
2．原式=a2-[a2-a2+a+2a2-a-a2]．
=a2-2a2=-a2
3．∵2x2+3x-6=Ax2-2Ax+A+Bx-B+C
∴
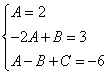
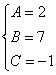
4．因8x2+2x-5-5x2+x-3=3x2+3x-8
∴另一个多项式为：3x2+3x-8
5．A+B=5x2-mx+n+（-3y2+2x-1）=5x2-3y2-mx+2x+n-1
由题意
∴m2-2mn+n2=（m-n）2=1
6．4 7．（1）5、7、9 （2）15 （3）2k-1
第4课 整式的乘除
目的：复习幂的运算法则，整式的乘除运算．
中考基础知识
1． 幂的运算法则：am·an=______（m，n都是正整数），
（am）n=_______（m，n都是正整数）．
am÷an=_______（m，n都是正整数，且m>n，a≠0），
（ab）n=______（n为正整数）．
2．整式的乘除
（1）单项式×单项式：4a2x5·（-3a3bx）=_________，
（2）单项式×多项式：m（a+b+c）=__________，
（3）多项式×多项式：（a+b）（m+n-d）=_______．
（4）单项式÷单项式：-12a5b3x2÷4a3x2=________．
3．乘法公式
（1）平方差公式：（a+b）（a-b）=________．
（2）完全平方公式：（a+b）2=_______，（a-b）2=_________．
（3）立方和、立方差公式：（a+b）（a2-ab+b2）=________，__________=a3-b3
4．在做整式乘除时，严格按照运算法则进行，做每一步都应有计算依据，充分利用乘法公式简化计算．
备考例题指导
例1．下列计算正确的是（ ）
（A）x5+x5=x10 （B）（3ab2）3=9a3b6
（C）a2·a3=a6 （D）（-c）6÷（-c）5=-c（c≠0）
选（D）
例2．（2005，金华市）如图，沿正方形的对角线对折，把对折后重合的两个小正方形内的单项式相乘，乘积是___________（只要写出一个结论）
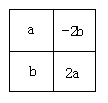
答案：2a2或-2b2任写一个．
例3．化简（a-b）3·（b-a）2÷（b-a）3．
分析：底数不同，不能直接乘除，但注意到a-b与b-a是互为相反数，
而且（a-b）3=-（b-a）3
解：原式=-（b-a）3·（b-a）2÷（b-a）3
=-（b-a）3+2-3 （注意乘除在一起要依次运算）
=-（b-a）2
例4．计算（1）（-2b-5）（2b-5）；
（2）（a+b-1）（a-b+1）．
分析：在（a+b）（a-b）=a2-b2中，其左边的两个多项式有两项（a与a）相同，有两项b与-b是互为相反数．这里平方差公式的使用条件．
解：（1）原式=（-5）2-（2b）2=25-4b2．
（2）原式=[a+（b-1）][a-（b-1）]
=a2-（b-1）2
=a2-（b2-2b+1）
=a2-b2+2b-1
备考巩固练习
1．填空题
（1）-x3·（-x）5=________;[（-x）3]2·（-x）3=________;（-2x2y3）2·（-xy）3=________．
（2）-6x（x-2y）=_______;（x-6）（x+7）=________;（x-2）（x-y）=________．
（3）（2x-3y）2=________;（3a+b）2=________．
（4）（x+1）（x2-x+1）=_______;（_______-2b）（_______）=a3-（________）．
（5）若4m·8m-1÷2m=32，则m=________．
2．选择题
（1）下列各式中，计算正确的是（ ）
（A）a2·a3=a6 （B）a3÷a2=a2 （C）（a2）3=a6 （D）（3a2）4=9a8
（2）（2005，黄冈）下列计算中正确的是（ ）
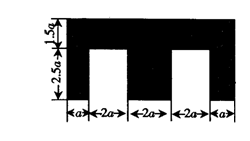（A）x5+x5=2x10
（B）-（-x）3·（-x）5=-x8
（C）（-2x2y）3·4x-3=-24x3y3
（D）（x-3y）（-x+3y）=x2-9y2
3．（2004，太原市）某公园一块草坪的形状如图所示（阴影部分），用代数式表示它的面积为__________．
4．化简求值：（a+2b）（a2+4b2）（a-2b），其中a=2，b=-．
5．解答下列各题：
（1）若a-
=3，求a2+
的值．
（2）若3x2-mxy+6y2是一个完全平方式，求m的值．
（3）已知x+y=2，xy=，求x3+y3的值．
（4）计算（8x2m-3-6xm+2-4xm）÷（-2xm-3）．
6．（2003，四川）观察下面的式子：
31=3，32=9，33=27，34=81，35=243，36=729，37=2187，38=6561，39=19683，……它们的个位数字的变化有一定规律，用你发现的规律直接写出910的个位数字是几？
7．（2005，苗城）先化简后求值：[（x-y）2+（x+y）（x-y）]÷2x，其中x=3，y=1.5
答案:
1．（1）x8；-x9；-x7y9
（2）-6x2+12xy；x2+x-42；x2-xy-2x+2y
（3）4x2-12xy+9y2，9a2+6ab+b2
（4）x3+1；（a-2b）（a2+2ab+b2）=a3-8b3
（5）22m·23m-3÷2m=25，m=2
2．（1）D （2）C 3．22a2
4．原式=（a2-4b2）（a2+4b2）=a4-16b4，当a=2，b=-
原式=24-16×（-）4=16-1=15
5．（1）由a-=3得（a-）2=9
∴a2-2+=9 ∴a2+=11
（2）∵3x2-mxy+6y2=（x）2-mxy+（
y）2
∴m=±2·=±6
或用△=0，求m．
（3）x3+y3=（x+y）（x2-xy+y2）=（x+y）[（x+y）2-3xy]
=2（22-3×）=2×
=5
（4）原式=-4xm+3x5+2x3
6．1
7．原式=1.5
第5课 因式分解
目的：了解因式分解的意义，区别因式分解与整式乘法，掌握因式分解的方法，能选择适当方法进行因式分解．毛
中考基础知识
1．因式分解定义：把一个多项式化成几个_______式乘积的形式．因式分解与整式的乘法是互为________．
2．因式分解的方法
（1）提取公因式法（首先考虑的方法）、应用公式法、分组分解法、十字相乘法．
（2）公式：a2-b2=_______，a2±2ab+b2=_______，a3+b3=________，a3-b3=________．
（3）二次三项式ax2+bx+c在实数范围分解为：ax2+bx+c=a（x-x1）（x-x2），其中x1、x2是方程ax2+bx+c=0的二根．
3．因式分解的一般步骤
先看有没有公因式，若有立即提出；然后看看是几项式，若是二项式则用平方差、立方或立方差公式；若是三项式用完全平方公式或十字相乘法；若是四项及以上的式子用分组分解法，要注意分解到不能再分解为止，还要注意题目要求什么范围内分解．
如x4-4=（x2+2）（x2-2）（在有理数范围内分解）
=（x2+2）（x+）（x-）（在实数范围内分解）
一般没有作说明，都只分解到有理数范围内．
4．因式分解是式的变形的基本功，用处很大，必须熟练掌握，分解时要快而准．
备考例题指导
例1．分解因式
（1）m2（m-n）2-4（n-m）2．
解：原式=m2（m-n）2-4（m-n）2
=（m-n）2（m2-4）
=（m-n）2（m+2）（m-2）
（2）2a（x-y）3+2a3（y-x）．
解：原式=2a（x-y）[（x-y）2-a2]
=2a（x-y）（x-y+a）（x-y-a）
例2．分解因式
（1）-2x3+3x2-x．
解：原式=-x（2x2-3x+1）
=-x（2x-1）（x-1）
（2）-xn+4+xn+1．
解：原式=-xn+1（x3-1）
=-xn+1（x-1）（x2+x+1）
说明：首项为负要提出负号，提取公因式时，另一个因式中不要漏掉1．
例3．在实数范围内分解因式
（1）2x4-19x2+9．
解：2x2 -1
x2 -9
原式=（2x2-1）（x2-9）
=（x+1）（x-1）（x+3）（x-3），
（2）2x2-8x+5．
解：原式=2（x-x1）（x-x2）
=2（x-
）（x-
）．
例4．若3x2-4x+2m在实数范围内可分解因式，求m的取值范围．
解：△=（-4）2-4×3×2m≥0，
即m≤．
备考巩固练习
1．选择题
（1）（2005，绵阳）对x2-3x+2分解因式，结果为（ ）
（A）x（x-3）+2 （B）（x-1）（x-2）
（C）（x-1）（x+2） （D）（x+1）（x-2）
（2）（2005，盐城）下列因式分解中，结果正确的是（ ）
（A）x2-4=（x+2）（x-2） （B）1-（x+2）2=（x+1）（x+3）
（C）2m2n-8n3=2n（m2-4n2） （D）x2-x+=x2（1-+
）
（3）（2005，四川）把多项式ac-bc+a2-b2分解因式的结果是（ ）
（A）（a-b）（a+b+c） （B）（a-b）（a+b+c）
（C）（a+b）（a-b-c） （D）（a+b）（a-b+c）
（4）下列因式分解中，错误的是（ ）
（A）2a3-8a2+12a=2a（a2-4a+6） （B）x3-5x-6=（x-2）（x-3）
（C）-x3+3x2-x=x（2x-1）（x-1） （D）x2+xy+xz+yz=（x+y）（x+z）
2．在实数范围内分解
（1）x4-11x2+18
（2）2x2+7xy-y2
3．若（x-3）是kx4+10x-192的一个因式，求k的值．
4．若3，-2是一元二次方程4x2+bx+c=0的二根，则二次三项式4x2+bx+c可分解成什么．
5．计算：（1）（a-b）÷（+
）；（2）（a-2
+b）÷（-）．
6．（1）解一元二次方程x2-5x+6=0． （2）分解因式kx2-（k+m）x+m．
7．要使二次三项式x2+mx-6能在整数范围内分解因式，求整数m的值．
答案:
1．（1）B （2）A （3）A （4）B
2．（1）原式=（x2-2）（x2-9）=（x+）（x-）（x+3）（x-3）
（2）原式=2（x-
y）（x-
y）（不要忘了带上y）
3．令kx4+10x-192=0，则x=3是这个方程的一个根．把x=3代入得k=2
4．4x2+6x+c=4（x-3）（x+2）
5．（1）原式=（+）（-）÷（+）=-
（2）原式=（-）2÷（-）=-
6．（1）（x-2）（x-3）=0，x1=2，x2=3
（2）∴原式=（kx-m）（x-1）（用十字相乘法）
7．∵-6可分解为：-6×1，-1×6，-2×3，-3×2
∴m=-6+1，-1+6，-2+3，-3+2
m=-5，5，1，-1.毛
第6课 分式的乘除
目的：了解分式意义，掌握分式基本性质，分式的乘除运算．毛
中考基础知识
1．分式值为0
分母≠0，分子=0；分式有意义分母≠0；分式无意义分母=0．
2．分式基本性质：-
=
，=
（m≠_______）
3．符号法则：-=-
=+=+
4．分式的乘除法：·
=
，÷
=·
=
分式的乘法实质上就是：分子与分母分别相乘，然后约分．
备考例题指导
例1．若分式
的值为0，则x的值等于（ ）
（A）±1 （B）8 （C）8或-1 （D）1
分析：分子=0，分母≠0，选（B）．
例2．计算：
÷
÷
．
分析：除法转化为乘法，然后分解因式约分．
答案：1．
例3．已知
=+
，求+
的值．
分析：用分析综合法解：已知→可知需解←求解
解：由已知得=
（a+b）2=ab
∴+=
=
=
=-1（注意配方）
例4．已知a=-，b=，求代数（a-b-
）·（a+b-
）的值．
分析：一般先化简，再代值计算，化简时，把a-b和a+b视为
和
，同时将b-a转化为-（a-b），通分先加减后乘．
解：原式=（+
）（-）
=
·
=
·
=（a+b）（a-b）=a2-b2
当a=-，b=时，
原式=（-）2-（）2=
-=．
备考巩固练习
1．选择题
（1）（2004，山西）下列各式与
相等的是（ ）
（A）
（B）
（C）
（x≠y） （D）
（2）（2005，河池市）如果把分式
中的x和y的值都扩大了3倍，那么分式的值（ ）
（A）扩大3倍 （B）扩大2倍 （C）扩大6倍 （D）不变
（3）（2005，武汉市）计算（1-
）（-1）的正确结果是（ ）
（A）
（B）- （C）
（D）-
2．已知x=
，求函数y=
的函数值．
3．化简（1）
·
÷
；
（2）
·
÷
。
4．若x2-3x+1=0，求x2+
的值．
5．若x：y：z=2：4：6，求
的值．
6．已知a-2b=2（a≠1），求代数式
-a2+4ab-4b2的值．
7．已知代数式
÷
+
，其中x=，求这个代数式的值．
8．已知a、b、c均不等于0，且++
=0，求证：a2+b2+c2=（a+b+c）2．
9．（2003，湖南湘潭）先化简，再计算：
-
，其中：x=5，y=-3．
10．有这样一道题：“计算：
÷
-x的值，其中x=2006”，有同学把“x=2006”错抄成“x=2060”，但是他的计算结果也是正确的，你说这是怎么回事？
答案：
1．（1）C （2）D （3）B
2．x=（+1）=2+
∴2x-1≠0，∴=
=x-2=
3．（1）原式=
·
·
=a+5
（2）原式=
·
·
=
4．由x2-3x+1=0两边同除以x得x-3+=0
x+=3，x2++2=9 ∴x2+=7
5．由已知设x=2k，则y=4k，z=6k
代入原式=
=
=-
6．原式=
-(a-2b)2
=
-22=-4=-
（整体代换思想）
7．原式=
·
+=+=
当x=时，原式=
=
=-4
8．由++=0，得bc+ac+ab=0
∴右边=a2+b2+c2+2ab+2bc+2ac
=a2+b2+c2+2（ab+bc+ac）
=a2+b2+c2
∴右边=a2+b2+c2=左边，∴等式成立．
9．解：原式=
-
=
-
=
=x-y
当x=5，y=-3时，原式=5+3=8
10．原式化简值恒为0，与x的取值无关。毛
第7课 分式的加减
目的：掌握分式的通分、加减运算．毛
中考基础知识
1．通分：将异分母的分式化成______叫做分式的通分．
2．同分母分式相加减：分母_______，分子________，最后还要________．
3．异分母分式相加减：先_______，然后分母________，分子_________，最后仍要________．
4．分式的综合运算注意顺序，尽量用运算律简化运算．
备考例题指导
例1．计算a2-a+1-
．
分析：把a2-a+1看做一个整体，看做分母为1的分式，通分后可利用立方和公式计算．
解：原式=
-=
-=
=
例2．化简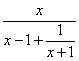
．
分析：用分式基本性质，在分子分母上同乘以x+1比较简便，这是化简繁分式的一般方法．
解：原式=
=
=
．
例3．错误辨析：有同学这样计算下题，指出他错在哪里，错误原因何在．
计算
+
-
．
解：原式=
-
-
=7（a+2）-12×2-6（a-2）
=7a+14-24-6a+12
=a+2
答：该同学在计算第二步时，去掉了分母，发生了严重错误，原因是他把分式计算与解分式方程混淆了．
注意：分式计算不能去分母，只能通分约分，而解分式方程，才可以去分母．
例4．计算
+
-
．
解：原式=
+
-
（分解分母）
=
+
-
（通分）
=
（分母不变，分子相加减）
=
（合并分子）
=
（分解分子）
=
（化简）
例5．已知
=
，求（2+x）（2+y）+x2的值．
分析：双向化简，整体代换思想体现，数学基本功──式的恒等变形．
解：由已知得（1+x）（1+y）=（1-x）（1-y），
1+x+y+xy=1-x-y+xy，
∴x+y=0．
∴（2+x）（2+y）+x2=4+2（x+y）+xy+x2
=4+xy+x2
=4+x（x+y）=4
备考巩固练习
1．计算（1）
-
+
．
（2）
·（1-）÷（1+
）．
（3）（
-
）÷
+
．
（4）+
+
+
（注意方法）．
2．先化简，再求值（
-
）÷
，其中a满足a2+2a-1=0．
3．先化简，再选取一个使原式有意义，而你又喜欢的数代入求值：
-
．
4．当a=时，求
-
的值．
5．（1）计算
+
-
．
（2）解方程+-=0．
6．（2005，绍兴）已知P=
-
，Q=（x+y）2-2y（x+y），小敏、小聪两人在x=2，y=-1的条件下分别计算了P和Q的值，小敏说P的值比Q大，小聪说Q的值比P大，请你判断谁的结论正确，并说明理由．
答案：
1．（1）原式=
-
+
=
=
=
（2）原式=
·
÷
=
··=
（3）原式=[
-
]·
+
=
·
+
=
+
=
（4）原式=
+
+
+
=
++
=
++
=
+=
2．原式=[
-
]·
=
·=
=
当a2+2a-1=0时，原式=1
3．原式=
+
=x+x-1=2x-1
令x=2，得原式=2×2-1=3
4．原式=
-
=-2（1+）-（-1）
=-2-2-2+=-4-
5．（1）原式=
=
=
（2）方程两边同乘以（x-1）去分母得
x2-2x+1+5x+5-4=0
x2+3x+2=0
x1=-1（舍），x2=-2，∴x=-2是原方程的解．
6．解：P=x+y，Q=x2-y2，当x=2，y=-1时，P=1，Q=3，Q>P，
所以小聪的结论是正确的．毛
第8课 二次根式
目的：了解二次根式、最简二次根式、同类二次根式的概念，会辨别最简二次根式和同类二次根式，掌握二次根式的加、减、乘、除运算，会分母有理化．毛
中考基础知识
1．二次根式定义：式子（_____）叫做二次根式．
2．二次根式的性质：（1）（）2=_____，
=_____=
（2）=·（______），
=
（_____）
3．最简二次根式：符合条件（1）被开方式中不含________，（2）被开方式中不含_________，符合以上两个条件的二次根式叫最简二次根式．
4．同类二次根式：化成_______式后，被开方式相同的二次根式叫做同类二次根式．
5．二次根式的运算：（1）加减运算：化成_________式后，再合并_______式．
（2）乘除运算：按·=，=运算，再化成_________二次根式．
6．分母有理化：（1）互为有理化因式：两个带有二次根式的代数式相乘不再含有_________，则这两个代数式叫做互为有理化因式，常见的有理化因式有：与_______，a+与_______，+与_______，m+n与_________．
（2）分母有理化：把分母中的根号________叫做分母有理化，方法是在分子分母上同乘以_________的有理化因式．
7．充分利用a=（）2 （a≥0）
a-b=（+）（-） （a≥0，b≥0）
备考例题指导
例1．把a·
的根号外的a移到根号内得（ ）
（A） （B）- （C）-
（D）
分析：∵->0 ，∴a<0
∴将根号外的a放进根号内时，应把负号留在外面，故选（C）
例2．若式子
有意义，则x的取值范围为（ ）
（A）x≥2 （B）x≠3 （C）x≥2或x≠3 （D）x≥2且x≠3
分析：（A）只考虑分子，（B）只考虑分母，（C）用“或”字不对，故选（D）．
例3．若最简二次根式
与
是同类二次根式，求x-x+1的值．
分析：由同类二次根式定义，将原题转化为解下列方程组
求出x，y值，在求x2-x+1时可用配方法．答案：x2-x+1=3．
例4．计算（1）-42+-2+
-2sin60°
解：原式=-16+2-++1-×2=-13-．
（2）
+
-
解：原式=
-
-
=4+
---3+=1．
（3）（3+-）（3-+）．
分析：用平方差公式，完全平方公式．
解：原式=[3+（-）][3-（-）]=9-（-）2=9-（7-2
）
=9-7+2=2+2．
（4）已知a=
，b=
，求
的值．
分析：先将a、b化简，再把的分母配方后再代值较简便．
解：a=（-1）2=3-2，
b=（+1）2=3+2，
∴a+b=6，
ab=（3-2）（3+2）=9-8=1．
原式=
=
=
=
．
备考巩固练习
1．填空题：（1）的整数部分为a，小数部分为b，则
-a=________．
（2）x、y都为实数，且y>
+
+2，化简
·
=________．
（3）a<0，化简
=________，如果
=
，则a的取值范围为_______．
（4）最简根式
和
是同类根式，则a=__________，b=__________．
（5）函数y=
中的自变量x的取值范围是________．
（6）xy<0，化简
=_________．
2．已知x=-1，y=+1，求
+
的值．
3．计算
-
÷（
+
）．
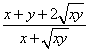4．若m，n是方程x2-3x+3=0的两个根，求
-
的值．
5．计算（1）
-
；（2）（a-b）÷（a+b+）。
6．当a=cos30°，b=sin45°时，求
（
-
）÷（
-
）的值．
7．（2005，烟台）已知a=，求
-
．
答案：
1．（1） （2）2
（3）-a
，-3<a≤0
（4）1，1
（5）x>4 （6）-x
2．∵x=-1，y=+1
∴x+y=2，xy=1
∴+=
=
=
=6
3．原式=
-
·
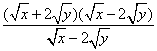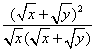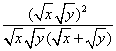
=+2-
·
=+2-
=+
4．∵m，n是方程x2-3x+3=0的两个根
∴m+n=3，mn=3
又∵（-）2=-2+=
-2=
-2=2
∴-=±
5．（1）原式=
-
=
=4
（2）原式=
=
=
6．原式=[-
]÷（-）
=
÷
=
÷
=
=
当a=cos30°=，b=sin45°=时
原式=
=
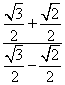=5+2
7．原式=-2-1。毛
热点1 实数与实数的运算
（时间：100分钟 分数：100分）
一、选择题（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一个是符合题目要求的）
1．实数，
，
中，分数的个数是（ ）
A．0 B．1 C．2 D．3
2．-3的绝对值是（ ）
A．3 B．-3 C． D．-
3．4的平方根是（ ）
A．±2 B．2 C．2 D．16
4．ab≠0，则等式│a+b│=│a│+│b│成立的条件是（ ）
A．a>0，b<0 B．ab<0 C．a+b=0 D．ab>0
5．某城市科技园超级计算机中心内，被称为“神州1”的计算机速度为每秒384000 000 000，保留四个有效数字，用科学记数法表示每秒运算的次数是（ ）
A．3.84×1011 B．3.840×1011 C．3.84×1012 D．3.840×1012
6．一张纸的厚底约是0.1毫米，而一层办公楼的高度大约是4米，假设有一张足够大的纸将其对折20次以后，大约相当于（ ）层楼房高．
A．26 B．2 C．0.2 D．0.02
7．已知数轴上点A、点B所表示的数分别是a、b，点A到原点距离是5，点B到原点的距离是1，则线段AB的长度是（ ）
A．6 B．4 C．6或4 D．以上均错
8．下列语句：①不循环小数是无理数；②两个无理数的和还是无理数；③有理数与无数数的和是无理数；④两个无理数之积一定是无理数；⑤无理数与有理数之积可能是有理数．其中错误的有（ ）
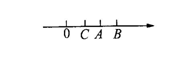A．2个 B．3个 C．4个 D．5个
9．如图1-1，数轴上表示1，的对应点分别是A，B，点B关于A的对称点为C，则点C所表示的数是（ ）
A．-1 B．1- C．2- D．-2
10．将1，-2，3，-4，5，-6，…，按一定规律排列如下：
1
-2 3 -4
5 -6 7 -8 9
-10 11 -12 13 -14 15 -16
则第10行从左至右第9个数是（ ）
A．90 B．-90 C．-89 D．89
二、填空题（本大题共8小题，每小题3分，共24分）
11．比较大小：______1.141，_____
．
12．利用计算器计算
+（）3的按键顺序是_______．
13．绝对值小于2 005的所有实数的和是_________．
14．已知2+=22×，3+
=32×，4+
=42×，…，若10+=102×（a，b为正整数），则a+b_____．
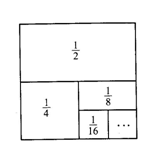15．我国著名数学家华罗庚曾说过：“数形结合百般好，隔裂分家万事休．”如图1-2，在边长为1的正方形纸板上，依次贴面积为，，，…
，的矩形纸片（n为大于1的整数），请你用“数形结合”的思想，计算+++…+=_______．
16．任意找一个3的倍数的数，先把这个数的每一个数字都立方，再相加，得到一个新数，然后把新数的每一个数位上的数字再立方，求和……重复运算下去，就能得到一个恒定的数字T=________．
17．已知数x的平方根是2m+1与-3m+5，则x=_______．
18．作图题：请在图1-3所示的数轴上作出表示-
的点．
三、解答题（本大题共46分，19～23题每题6分，24题、25题每题8分．解答题应写出文字说明、证明过程或演算步骤）
19．玩24点游戏，对下面一组牌，请你给出运算符号，使结果为24．
（1）2 4 7 11． （2）2 6 4 2．
20．计算：
（1）（-125）×（-
）×（-8）×2； （2）（-8
）×（-15）-15×（-9）．
21．化简：
（1）（+）（-）+（
-）2;
（2）（-3）0-（）-2+（-1）3-sin245°．
22．小王上周五在股市以收盘价（收市时的价格）每股25元买进某公司股票1000股，在接下来的一周交易日内，小王记下该股每日收盘价格相比前一天的涨跌情况（周六、周日不交易，单位：元）．
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌（元） | +2 | -0.5 | +1.5 | -1.8 | +0.8 |
根据上表回答问题：
（1）星期三收盘时，该股票每股多少元？
（2）本周内该股票收盘时的最高价、最低价分别是多少？
（3）已知买入股票与卖出股票均需支付成交金额的5‰的交易费．若小王在本周五以收盘价将全部股票卖出去，它的收益情况如何？
23．有若干个数，第一个数记为a1，第二数为a2，第三个数记为a2，…，第n个数记为an，若a1=-，从第二个数起，每个数都等于“1与它前面那个数差的倒数”，试计算：
（1）a2，a3，a4;（2）a2000，a2001．
24．甲、乙、丙三个小朋友同时到一个水龙头前排队打水，甲打满一桶水需要3分钟，乙打满一桶水需2分钟，丙打满一桶水需1分钟、打满水的人先走，则有哪几种排列方案？哪种排队方案使得三人等待时间和最小？等待时间和是多少？
25．先阅读下面的材料，然后解答问题：
在一条直线上有依次排列的n（n>1）台机床在工作，我们要设置一个零件供应站P，使这n点机床到供应站P的距离总和最小，要解决这个问题，先“退”到比较简单的情形．
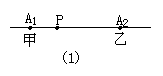
如图1-4（1），如果直线上有2台机床时，很明显设在A1和A2之间的任何地方都行，因为甲和乙所走的距离之和等于A1到A2的距离．
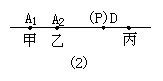
如图1-4（2），如果直线上有3台机床时，不难判断，供应站设在中间一台机床A2处最合适．因为如果P放在A2处，甲和丙所走的距离之和恰好为A1到A3的距离，而如果把P放在别处，例如D处，那么甲和丙所走的距离之和仍是A1到A3的距离，可乙还是走A2至D的这一段，这是多出来的．因此P放在A2处是最佳选择．
不难知道，如果直线上有4台机床，P应设在第2台与第3台之间的任何地方；有5台机床，P应设在第3台位置．
（1）有n台机床时，P应设在何处？
（2）根据（1）的结论，求│x-1│+│x-2│+│x-3│+…+│x-617│的最小值．
答案:
一、选择题
1．B 2．A 3．A 4．D 5．B 6．A 7．C 8．B 9．C 10．B
二、填空题
11．>，< 12．略 13．0 14．109 15．1-
16．153 17．169 18．略
三、解答题
19．解：（1）2+4+7+11=24．（2）2×6×4÷2=24．
20．解：（1）-400．（2）270．
21．解：（1）原式=2++2-2=．
（2）原式=1-4+（-1）-=-
．
22．解：（1）每股为：25+2-0.2+1.5=28（元）．
（2）最高价为：25+2-0.5+1.5=28（元）．
最低价为：25+2-0.5+1.5-1.8=26.2（元）．
（3）收盘价为：25+2-0.5+1.5-1.8+0.8=27（元）．
收益为：27×1000-25×1000-25×1000×0.005-27×1000×0.005=1740（元）．
赚了1740元．
23．解：（1）a2=
，a3=
=3，a4=-．
（2）a2000=，a2001=3．
24．解：有六种排队方案，分别为甲丙乙、甲乙丙、乙甲丙、乙丙甲、丙甲乙、丙乙甲．
等待时间和最小的排队方案是丙乙甲，
此时丙等待1分钟，乙等待3分钟，甲等待6分钟，共等待10分钟．
25．解：（1）当n为偶数时，P应设在
台与（+1）台之间的任何地方；
当n为奇数时，P应设在第
台处．
（2）95 172．
热点2 代数式的变形与代数式的求值
（时间：100分钟 分数：100分）
一、填空题（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一个是符合题目要求的）
1．在x，，
，x+y，xy-2，
中，单项式有（ ）
A．2个 B．3个 C．4个 D．5个
2．x的5倍与y的差等于（ ）
A．5x-y B．5（x-y） C．x-5y D．x5-y
3．用正方形在日历中任意框出的四个数一定能被（ ）整除
A．3 B．4 C．5 D．6
4．现规定一种运算：a*b=ab+a-b，其中a、b为常数，则2*3+1*4等于（ ）
A．10 B．6 C．14 D．12
5．已知一个凸四边形ABCD的四条边长依次是a、b、c、d，且a2+ab-ac-bc=0，b2+bc-bd-cd=0，那么四边形ABCD是（ ）
A．平行四边形 B．矩形 C．菱形 D．梯形
6．若m2x2-2x+n2是一个完全平方式，则mn的值为（ ）
A．1 B．2 C．±1 D．±2
7．某商店有两个进价不同的计算器都卖了64元，其中一个赢利60%，另一个亏本20%，在这次买卖中这家商店（ ）
A．赔38元 B．赚了32元 D．不赔不赚 D．赚了8元
8．要使
的值为0，则m的值为（ ）
A．m=3 B．m=-3 C．m=±3 D．不存在
9．已知
+
+
的值为正整数，则整数x的值为（ ）
A．4 B．5 C．4或5 D．无限个
10．已知有理数a、b满足ab=1，则M=
+
，N=
+
的大小关系是（ ）
A．M>N B．M=N C．M<N D．不确定
二、填空题（本大题共8小题，每小题3分，共24分）
11．如果a、b、c为互不相等的实数，且满足关系式b2+c2=2a2+16a+14，bc=a2-4a-5，那么a的取值范围是______．
12．若单项式-2a2m-1b2与abn-3的和仍是单项式，则m+n________．
13．xa=4，xb=3，则xa-2b=________．
14．已知a≠o，化简
=_________．
15．已知x+5y=6，则x2+5xy+30y=_________．
16．已知：
（x-1）（x+1）=x2-1，
（x-1）（x2+x+1）=x3-1，
（x-1）（x3+x2+x+1）=x4-1，
……
根据以上规律试写出下题结果：
（x-1）（xn+xn-1+xn-2+…+x+1）=________．
17．某商店原价a元，因需求量大，经营者两次提价，每次提价10%；后经市场物价调整，又一次降价20%，降价后这种商品的价格是__________元．
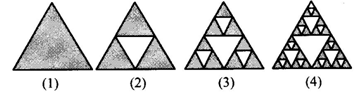
18．观察图2-1，若第1个图形中的阴影部分的面积为1，第2个图形中的阴影部分面积为，第3个图形中的阴影部分面积为
，第4个图形中阴影部分的面积为
，…，则第n个图形的阴影部分的面积为_________．
三、解答题（本大题共46分，19～23题每题6分，24题、25题每题8分，解答题应写在文字说明、证明过程或演算步骤）
19．利用简便方法计算：
（1）20002-2001×1999． （2）9992．
20．化简：
（1）
+
÷
；
（2）
-
×．
21．已知-x=2，求x2+的值．
22．分解因式：
（1）3（a-b）2+6（b-a）；
（2）（x+1）（x+2）+．
23．某地电话拨号入网有两种收费方式，用户可任选其一：（A）计时制，0.05元/分；（B）包月制，50元/月（只限一部宅电上网）．此外，每种上网方式都得加收通讯费0.02元/分．
（1）某用户平均每月上网x小时，请你帮他计算一下应该选择哪种收费方式合算．
（2）若x=20时，则你帮他选用的收费方式应缴多少钱？
24．小刚做了一道数学题：两个多项式A、B，其中B为4x2-5x-6，试求A+B．他误将“A+B”看作“A-B”，结果求得的答案是10x-7x2+12，由此你能求出A+B的正确答案吗？
25．扑克牌游戏，小明背对小亮，让小亮按下列四个步骤操作：第一步分发左、中、右三堆牌，每堆牌不少于两张，且各堆牌的张数相同；第二步从左边一堆拿出两张，放入中间一堆；第三步从右边一堆拿出一张，放入中间一堆；第四步左边一堆有几张牌，就从中间一堆拿几张牌放入左边一堆．这时小明准确地说出了中间一堆牌现有的张数，请你用所学的知识确定中间牌的张数．
答案：
一、选择题
1．C 2．A 3．B 4．B 5．A 6．C 7．D 8．B 9．C 10．B
二、填空题
11．a≥-1 12．6 13．
14．│a+│ 15．36
16．xn+1-1 17．0.968a 18．（）n-1
三、解答题
19．解：（1）原式=2 0002-（2 000+1）（2 000-1）=2 0002-2 0002+1=1．
（2）原式=（1 000-1）2=1 0002+1-2 000=998 001．
20．解：（1）
．（2）1．
21．解：由-x=2知（-x）2=4，
故+x2-2=4．所以+x2=6．
22．解：（1）原式=3（a-b）（a-b-2）．
（2）原式=x2+3x+
=（x+
）2．
23．解：（1）选用（A）方式应缴费（0.05+0.02）×60x=4.2x；
选用（B）方式应缴费为500+0.02×60x=50+1.2x．
当4.2x<50+1.2x，即x<
时选用（A）方式便宜；
当x>时，选用（B）方式合算；
当x=时选用（A）（B）两种方式一样．
（2）由于20>，所以选择（B）方式合算，费用为50+1.2×20=74元．
24．解：A+B=A-B+2B=10x-7x2+12+2（4x2-5x-6）=x2．
25．解：设第一步分发的左、中、右三堆牌的张数均为x张；则第二步左边一堆有（x-2）张，中间一堆（x+2）张，右边仍是x张；第三步左边有（x-2）张，中间有（x+3）张，右边为（x-1）张，第四步中间有[x+3-（x-2）]张，即5张牌．