中考数学数与式复习
一.教学内容：
数与式
二. 教学目标：
通过对数与式基础知识的复习，解决中考中常见的问题
三. 教学重点、难点：
熟练地解决数与式相关的问题
四. 课堂教学：
中考导航一
中考大纲要求一
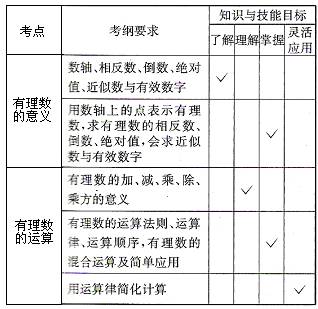
中考导航二
中考大纲要求二
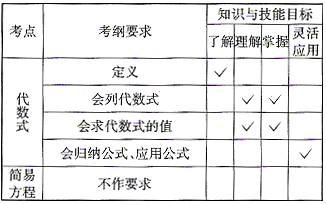
中考导航三
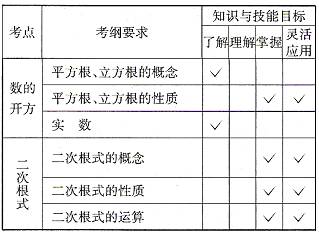
中考大纲要求三
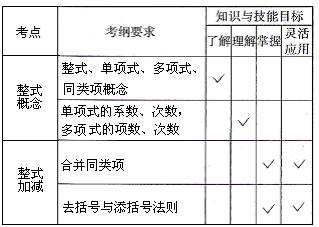
中考导航四
中考大纲要求四
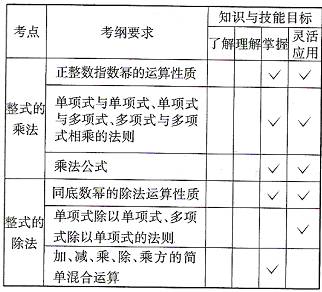
中考导航五
中考大纲要求五
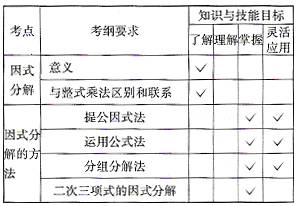
中考导航六
中考大纲要求六
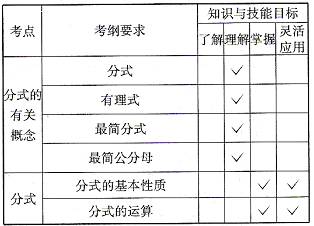
中考导航七
中考大纲要求七
【典型例题】
例1. 如果收入200元记作+200元，那么支出150元记作（ ）
A. +150元 B. –150元 C. +50元 D. –50元
答案：B
例2. 点A在数轴上表示+2，从点A沿数轴向左平移3个单位到点B，则点B所表示的实数是（ ）
A. 3 B. –1 C. 5 D. –1或3
答案：B
例3. -3的相反数是（ ）
A.
–3 B.
3 C.
D.
答案：A
例4. 下列计算正确的是（ ）
A.
B.
C. 
D.
答案：D
例5. 将
这三个实数按从小到大的顺序排列，正确的结果是（ ）
A.
B. 
C. 
D. 
答案：C
例6. 据2006年5月27日《沈阳日报》报道，“五·一”黄金周期间2006年沈阳“世园会”的游客接待量累计人次，用科学记数法表示为（ ）
A.
人次 B.
人次
C. 
人次 D.
人次
答案：C
例7. 下列计算错误的为（ ）
A.
B.
C. 
D.
答案：B
例8. 有一个数值转换器，原理如下：当输入的x为64时，输出的y是（ ）
A.
8 B.
C.
D.
答案：B
例9. 如图所示，每个正方形点阵均被一直线分成两个三角形点阵，根据图中提供的信息，用含n的等式表示第n个正方形点阵中的规律___________。
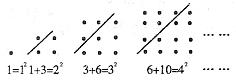
答案：
例10. 计算：
。
答案：
例11. 先化简，再求值：
，其中
。
答案：
【模拟试题】
一、选择题
1. 下表是5个城市的国际标准时间（单位：时），那么北京时间2006年6月17日上午9时应是（ ）
A. 伦敦时间2006年6月17日凌晨1时
B. 纽约时间2006年6月17日晚上22时
C. 多伦多时间2006年16日晚上20时
D. 汉城时间2006年6月17日上午8时
2. 下列计算正确的是（ ）
A. –3+2=1 B. -2=-2 C. 3×（-3）=-9 D. 20-1=1
3. –0.5的倒数是（ ）
A.
B.
C.
–2 D.
2
4. 下列四个数据，精确的是（ ）
A. 小莉班上有45人
B. 某次地震中，伤亡10万人
C. 小明测得数学书的长度为21.0cm
D. 吐鲁番盆地低于海平面大约155m
5. 估算
的值是（ ）
A. 在5和6之间 B. 在6和7之间
C. 在7和8之间 D. 在8和9之间
6. 根式
的值是（ ）
A. –3 B. 3或-3 C. 3 D. 9
7. 计算
的结果是（ ）
A.
B.
C.
D.
8. 把代数式
分解因式，结果正确的是（ ）
A.
B.
C. 
D.
9. 小王利用计算机设计了计算程序，输入和输出的数据如下：
那么，当输入数据为8时，输出的数据是（ ）
A.
B.
C.
D.
10. 根据下表中的规律，从左到右的空格中应依次填写的数字是（ ）
A. 100，011 B. 011，100 C. 011，101 D. 101，110
二、填空题
1. 在电视上看到的天气预报中，绵阳王朗国家级自然保护区某天的气温为“-5℃”，表示的意思是__________。
2. 的倒数是__________。
3. 用“
”定义新运算：对于任意实数a，b，都有ab=b2+1。例如，74=42+1=17，那么53=_________；当m为实数时，m（m2）=__________。
4. 我们常用的数是十进制的数，而计算机程序处理中使用的是只有数码0和1的二进制数。这两者可以相互换算，如将二进制数1101换算成十进制数应为
，按此方法，则将十进制数25换算成二进制数应为__________。
5. 用同样大小的正方形按下列规律摆放，将重叠部分涂上颜色，下面的图案中，第n个图案中正方形的个数是__________。
6. 若x=2，则
的值是__________。
7. 今年1～5月份，深圳市累计完成地方一般预算收入216.58亿元，数据216.58亿精确到__________。
8. 计算
的结果是__________。
9. 某天傍晚，北京的气温由中午的零上3℃下降了5℃，这天傍晚北京的气温是__________。
10. 如图所示，下列几何体是由棱长为1的小立方体按一定规律在地面上摆成的，若将露出的表面都涂上颜色（底面不涂色），则第n个几何体中只有两个面涂色的小立方体共有___________个。
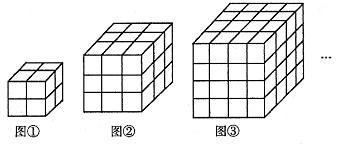
三、解答题
1. 计算：
。
2. 在下面两个集合中各有一些实数，请你分别从中选出2个有理数和2个无理数，再用“+，-，×，÷”中的3种符号将选出的4个数进行3次运算，使得运算结果是一个正整数。
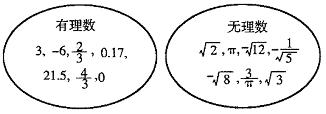
3. 先化简，再求值：
，其中
。
4. 对于试题：“先化简，再求值：
，其中x=2。”某同学写出了如下解答：
解：
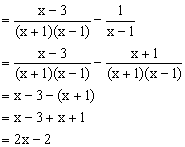
当x=2时，原式=2×2-2=2。
她的解答正确吗？如不正确，请你写出正确解答。
5. 课堂上，李老师给大家出了这样一道题：当x=3，
时，求代数式
的值。小明一看，“太复杂了，怎么算呢？”你能帮小明解决这个问题吗？请你写出具体过程。
【试题答案】
一、1. A 2. C 3. C 4. A 5. C
6. C 7. C 8. C 9. C 10. B
二、1. 零下5摄氏度 2. –2
3. 10，26 4. 11001
5. n+1 6. 1
7.
百万位 8.
9. 零下2° 10. 8n-4
三、1. –1
2.
3，0，
，
；3+0-
=3+0+
=3+4=7
3.
4. 解：她的解答不正确。正确解答如下：
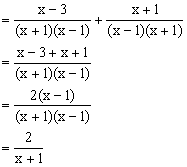
当x=2时，原式
5.
解：原式
所以，当
时，代数式的值都是。