中考数学模拟试题38
班级：_________ 姓名：_________ 得分：_________
一、填空题(每小题3分，共18分)
1．试写出一个解为
的二元一次方程组______．
2．已知等腰梯形的周长为80 cm，中位线长与腰长相等，则它的中位线长等于______cm．
3．在数据组-1，0，4，5，8中插入一数据x，使该数据组的中位数为3，则x＝______．
4．如图1，两建筑物AB和CD的水平距离为30米，从A点测得D点的俯角为30°，测得C点的俯角为60°，则建筑物CD的高为______米．
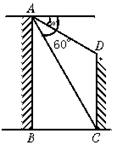
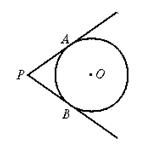
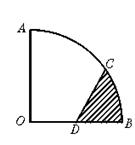
图1 图2 图3
5．如图2，PA，PB是⊙O的切线，A、B是切点，∠APB＝70°，点C是⊙O上异于A、B的任意一点，那么∠ACB＝______．
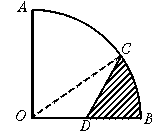
6．如图3，半径OA＝2 cm，圆心角为90°的扇形OAB中，C为
的中点，D为OB的中点，则图中阴影部分的面积为______cm2．
二、选择题(每小题3分，共12分)
7．如图4，从下列四个条件：①BC＝B′C，②AC＝A′C，③∠A′CA＝∠B′CB，④AB＝A′B′中，任取三个为题设，余下的一个为结论，则最多可以构成正确命题的个数是( )
A．1 B．2 C．3 D．4
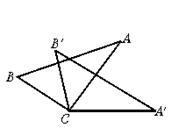
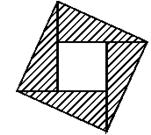
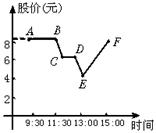
图4 图5 图6
8．2002年8月在北京召开的国际数学家大会会标如图5所示，它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形．若大正方形的面积是13，小正方形的面积是1，直角三角形的较长直角边为a，较短直角边为b，则a3＋b4的值为( )
A．35 B．43 C．89 D．97
9．若一元二次方程2x2-6x＋3＝0的两根为a 、b ，则(a -b )2的值为( )
A．24 B．18 C．6 D．3
10．某股票从9∶30到15∶00股价变化情况如图6，则表示股价上涨的是线段( )
A．BC B．DE C．AB D．CD E．EF
三、解答题(11～12每小题8分；13～18每小题9分，共70分)
11．已知：a＝2-
，b＝2＋，求
÷
的值．
12．解方程组
13．(1)如图7，E、F分别是正方形ABCD的边BC、CD上一点，AG⊥EF于点G，若AG＝AB．求证：EF＝BE＋DF．
(2)如图8，M是正方形PQRS的边QR上一点，仿第(1)题，在边SR上求作一点N，使MN＝QM＋SN(不写作法，保留作图痕迹)．
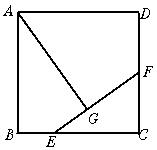
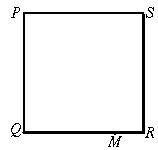
图7 图8
14．如图9，路灯沿灯罩边缘射出的光线与地面水平线的交点为A，∠A＝43°，A与灯柱底部B的距离5.5米，灯柱上方的横杆DE长0.5米，EF⊥AB于F．若EF所在直线是灯罩的对称轴，求灯柱BD上被灯光直接照射的BC的长(精确到0.01米)．
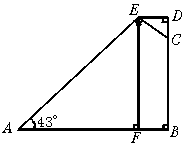
图9
15．已知二次函数y＝ax2＋bx＋c的图象过点A(2，0)，且与直线y＝-
x＋3相交于B、C两点，点B在x轴上，点C在y轴上．
(1)求二次函数的解析式；
(2)如果P(x，y)是线段BC上的动点，O为坐标原点，试求S△POA的面积S与x之间的函数关系式，并求出自变量的取值范围．
(3)是否存在这样的点P，使PO＝AO？若存在，求出P点的坐标；若不存在，请说明理由．
16．某农户在山上种了脐橙果树44株，现进入第三年收获，收获时，先随意采摘了5株果树上的脐橙称的每株果树上的脐橙重量如下：(单位：千克)35，35，34，39，37
(1)根据样本平均数估计这年脐橙的总产量约是多少？
(2)各市场上脐橙售价为每千克5元，则这年该农户脐橙收入是多少元？
(3)已知该农户第一年卖脐橙收入为5500元，估计第二年、第三年卖脐橙收入的平均增长率是多少？
17．如图10，已知：BC是⊙O的切线，⊙O的弦AB⊥OC，垂足为E，延长BO、CA交于P，PB与⊙O交于点D．
(1)求证：AC是⊙O的切线； (2)求证：2PD·BC＝PA·DB；
(3)如果PA＝
，⊙O的半径为2，设∠ABP＝a，求tana的值．
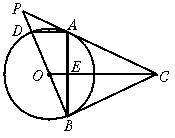
图10
18．下列图形中，图(a)是正方体木块，把它切去一块，得到如图(b)(c)(d)(e)的木块．
(1)我们知道，图(a)的正方体木块有8个顶点、12条棱、6个面，请你将图(b)、(c)、(d)、(e)中木块的顶点数、棱数、面数填入下表：
| 图号 | 顶点数x | 棱数y | 面数z |
| (a) | 8 | 12 | 6 |
| (b) | |||
| (c) | |||
| (d) | |||
| (e) |
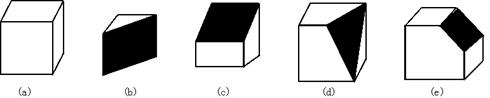
(2)上表，各种木块的顶点数、棱数、面数之间的数量关系可以归纳出一定的规律，请你试写出顶点数x、棱数y、面数z之间的数量关系式．
参考答案
一、1．
2．20 3．2 4．20
5．55°或125°
6．S扇形OBC＝
p r2＝
，S△OCD＝
OC·ODsin45°＝×2×1×
＝．
得S阴影＝-＝(p -2)．
二、7．B 8．B 9．D 10．E
三、11．ab，2 12．
13．(1)提示，连结AE、AF，可证△ABE≌△AGE，△ADF≌△AGF
(2)连结PM．
14．由题意，AF＝AB-FB＝AB-ED＝5．因为tan43°＝
，
所以EF＝AF·tan43°≈5×0.93＝4.65．
由∠AEF＝∠CEF＝∠ECD，∠AFE＝∠D，得△AEF∽△ECD．
因此，
，即
，
解得CD＝0.465．故BC＝BD-CD＝EF-CD＝4.65-0.465≈4.19(米)．
15．(1)二次函数的解析式为y＝
x2-
x＋3．
(2)∵ S△POA＝OA·y，
即S＝y，又P点在直线y＝-x＋3上，且0≤x＜4
∴ S＝-x＋3，0≤x＜4．
(3)设O到BC的距离为d，则BC2＝32＋42＝52，d·BC＝3×4，d＝
＞2，
而OA＝2，即PO的最小值大于AO．
∴ 不存在这样的点P，使PO＝AO．
16．(1)1584千克 (2)7920元 (3)20%
17．(1)连结OA，∵ AB⊥OC，OA＝OB，∴ ∠AOC＝∠BOC，
又∵ OC＝OC，∴ △AOC≌△BOC，
∵ BC是⊙O的切线，∴ ∠OBC＝90°
∴ ∠OAC＝90°，∴ AC是⊙O的切线．
(2)略
(3)∵ PC是⊙O的切线，PDB是⊙O的割线，∴ PA2＝PD·PB
∵ PA＝，PB＝PD＋BD＝PD＋4
∴ PD·(PD＋4)＝5．
∴ PD＝1或PD＝-5(舍去)．
∵ AD∥OC，∴ 
．
∴ ＝
，∴ AC＝2．
∵ PC、BC分别切⊙O于点A、B．∴ ∠PAD＝∠ABP．
∵ AD∥OC，∴ ∠PAD＝∠ACO．∴ ∠ABP＝∠ACO．
在Rt△OAC中OA＝2，AC＝2，∴ tana ＝
．
18．(1)图(b)填入6，9，5；图(c)填入8，12，6；图(d)填入8，13，7；
图(e)填入10，15，7
(2)x＋z＝y＋2(或x＋z-y＝2)．